Lời giải:
Vì $O,A,B$ thẳng hàng nên $AB$ là đường kính của đường tròn.
Cũng là 1 đoạn cong thuộc đường tròn, mà $AB$ là đoạn thẳng nên đáp án C bị loại
Vậy đáp án đúng là B.
Lời giải:
Vì $O,A,B$ thẳng hàng nên $AB$ là đường kính của đường tròn.
Cũng là 1 đoạn cong thuộc đường tròn, mà $AB$ là đoạn thẳng nên đáp án C bị loại
Vậy đáp án đúng là B.
Gọi Ot, Ot' là hai tia nằm trên cùng một nửa mặt phẳng bờ là đường thẳng xy đi qua O. Biết \(\widehat{xOt}=30^0,\widehat{yOt'}=60^0\). Tính số đo các góc \(\widehat{yOt},\widehat{tOt'}\) ?
Gọi O là một điểm nằm trên đường thẳng xy. Trên cùng một nửa măt phẳng bờ là xy. vẽ hai tia Ot và Oz sao cho xÔt=\(125^0\); xÔz=\(50^0\)
a)Tính yÔz
b)Tính zÔt
c)Gọi Om là tia đối của tia Oz. So sánh xÔz và mÔy
Trên đường thẳng xx' lấy điểm O sao cho góc xOy=40°, góc x'Oz=30°
a. So sánh góc xOy và x'Oz
b. Tính số đo góc yOz
c. Trên nửa mặt phẳng bờ xx' ko chứa tia Oy , vẽ tia Ot sao cho góc x'Ot = 40° . CTR tia Oy và tia Ot là 2 tia đối nhau
Cảm ơn mn nhiều !
Cho 10 đường thẳng cắt nhau tại O. Có tất cả bao nhiêu góc đỉnh O
Cho đường thẳng ạ // b và P1=O1=30°
a) viết lên một cặp góc đồng vị bằng nhau , khác nhau và nói số đó mỗi góc
b) viết tên hai cặp góc so le trong và nêu số đo mỗi góc
c) viết tên các cặp góc trong và nêu rõ số đo mỗi góc
Câu 4. Cho ba tia chung gốc Oa, Ob, Oc sao cho � o aOb 130 , � o bOc 140 , � o aOc 90 . Trong ba tia Oa, Ob, Oc tia nào nằm giữa hai tia còn lại? A. Tia Oa B. Tia Ob C. Tia Oc D. Không có tia nào. Câu 5. Cho hình vẽ. Các cặp góc bù nhau ở hình là: A. aAb � và bAd � B. aAc � và cAd � C. aAb � và bAc � D. cả A và B
:((
cho diểm B nằm giữa hai điểmA,C .Trên cùng một nửa mặt phẳng lấy điểm D,E sao cho ABD=64 độ ,ABE=117độ. hỏi trong ba tia BD,BE,BC tia nào nằm giữa hai tia còn lại??????????
a) Vẽ góc \(40^0\) có đỉnh là M trên giấy cứng. Cắt ra ta được một mẫu hình
b) Đóng hai chiếc đinh vào điểm A và B cách nhau 2,5cm. Đưa mẫu hình vào khe hở giữa hai chiếc đinh sao cho một cạnh sát A, một cạnh sát B. Khi đó đỉnh M của góc ở vị trí \(M_1\). Đặt mẫu hình nhiều lần để được nhiều vị trí \(M_1;M_2;M_3;....\) khác nhau của đỉnh M. Vậy ta có :
\(\widehat{AM_1B}=\widehat{AM_2B}=\widehat{AM_3B}=.....=40^0\)
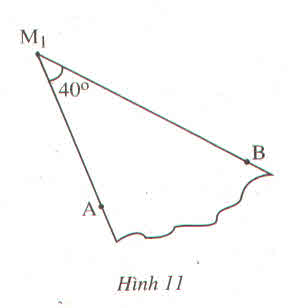
Đánh dấu khoảng 10 vị trí khác nhau của đỉnh M và dự đoán quỹ đạo của đỉnh M (h.11)
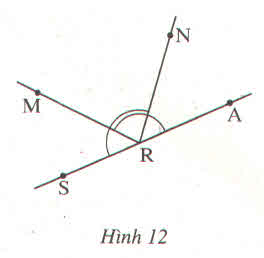
a) Vẽ hình 12 trong đó 3 điểm S, R, A thẳng hàng và \(\widehat{ARM}=\widehat{SRN}=130^0\)
b) Tính \(\widehat{ARN},\widehat{MRS},\widehat{MRN}\)
c) Dùng thước đo góc kiểm tra lại kết quả