cho hệ trục tọa độ có 3 điểm a (-1; 2), b (2 ;3) ,c (m; 0). tìm m để diện tích tam giác abc nhỏ nhất

Những câu hỏi liên quan
Trong không gian với hệ trục tọa độ Oxyz cho điểm M(3;-1;-2). Hình chiếu vuông góc của điểm M lên trục Oz là điểm có tọa độ
A. (3;0;0)
B. (0;-1;0)
C. (0;0;-2)
D. (3;-1;0)
cho mình hỏi vs
câu 1 trong không gian hệ trục tọa độ Oxyz cho mặt phẳng (A) đi qua hai điểm A( 2;-1;0) và có vecto pháp tuyến n (3:5:4)viết phương trình mặt cầu
câu 2 trong không gian với hệ trục tọa độ Oxyz cho mặt cầu (S) có tâm I(2;-3:7) và đi qua điểm M(-4:0;1) viết phương trình mặt cầu
Trong không gian với hệ trục tọa độ Oxyz, cho hai điểm là A(1;3;-1), B(3;-1;5). Tìm tọa độ của điểm M thỏa mãn hệ thức
M
A
→
3
M
B
→
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho hai điểm là A(1;3;-1), B(3;-1;5). Tìm tọa độ của điểm M thỏa mãn hệ thức M A → = 3 M B →
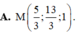
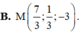
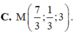
![]()
Trong không gian với hệ trục tọa độ Oxyz, cho hai điểm là A(1;3;-1), B(3;-1;5). Tìm tọa độ của điểm M thỏa mãn hệ thức
M
A
→
3
M
B
→
.
A.
M
5
3
;
13
3...
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho hai điểm là A(1;3;-1), B(3;-1;5). Tìm tọa độ của điểm M thỏa mãn hệ thức M A → = 3 M B → .
A. M 5 3 ; 13 3 ; 1 .
B. M 7 3 ; 1 3 ; - 3 .
C. M 7 3 ; 1 3 ; 3 .
D. M 4 ; - 3 ; 8 .
Trong không gian với hệ trục tọa độ Oxyz, cho điểm A(-3;2;-1). Tọa độ điểm A' đối xứng với A qua trục Oy là
A. A'(-3;2;1)
B. A'(3;2;-1)
C. A'(3;2;1)
D. A'(3;-2;-1)
Trong không gian với hệ tọa độ Oxyz cho hai điểm
A
-
1
;
-
1
;
0
,
B
3
;
1
;
-
1
. Điểm M thuộc trục Oy và cách đều hai điểm A, B có tọa độ là: A.
M
0...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz cho hai điểm A - 1 ; - 1 ; 0 , B 3 ; 1 ; - 1 . Điểm M thuộc trục Oy và cách đều hai điểm A, B có tọa độ là:
A. M 0 ; 9 2 ; 0
B. M 0 ; 9 4 ; 0
C. M 0 ; - 9 4 ; 0
D. M 0 ; - 9 2 ; 0
Trong không gian với hệ tọa độ Oxyz cho hai điểm A(-1;-1;0), B(3;1;-1). Điểm M thuộc trục Oy và cách đều hai điểm A, B có tọa độ là:
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz cho hai điểm A(-1;-1;0), B(3;1;-1). Điểm M thuộc trục Oy và cách đều hai điểm A, B có tọa độ là:

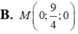
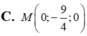

Cho hàm số y = x + 2 và hàm số y = 3 − x có đồ thị là (d1) và )(d2).
a) Vẽ (d1) và (d2) trên cùng một hệ trục tọa độ.
b) Tìm tọa độ giao điểm của (d1) với trục hoành.
c) Tìm tọa độ giao điểm của (d2) với trục tung.
d) Tìm tọa độ giao điểm của (d1) và (d2).
1. Trong hệ trục tọa độ Oxy có A(2;3) B(1;4), C(-1;-5)
tìm tọa độ điểm I trên AB sao cho \(\left|\overrightarrow{IA}+3\overrightarrow{IB}+5\overrightarrow{IC}\right|\) có giá trị nhỏ nhất
\(\overrightarrow{AB}=\left(-1;1\right)\) nên pt AB có dạng:
\(1\left(x-2\right)+1\left(y-3\right)=0\Leftrightarrow x+y-5=0\)
Do I thuộc AB nên tọa độ có dạng: \(I\left(a;5-a\right)\Rightarrow\left\{{}\begin{matrix}\overrightarrow{IA}=\left(2-a;a-2\right)\\\overrightarrow{IB}=\left(1-a;a-1\right)\\\overrightarrow{IC}=\left(-1-a;a-10\right)\end{matrix}\right.\)
\(\Rightarrow\overrightarrow{IA}+3\overrightarrow{IB}+5\overrightarrow{IC}=\left(-9a;9a-55\right)\)
\(\Rightarrow\left|\overrightarrow{IA}+3\overrightarrow{IB}+5\overrightarrow{IC}\right|=\sqrt{\left(9a\right)^2+\left(55-9a\right)^2}\ge\sqrt{\dfrac{1}{2}\left(9a+55-9a\right)^2}=\dfrac{55}{\sqrt{2}}\)
Dấu "=" xảy ra khi \(9a=55-9a\Rightarrow a=\dfrac{55}{18}\Rightarrow I\left(\dfrac{55}{18};\dfrac{35}{18}\right)\)
Kiểm tra lại tính toán
Đúng 2
Bình luận (0)
Trong không gian với hệ trục tọa độ Oxyz, cho các điểm A(-1;2;-3); B(2; -1; 0). Tọa độ của vectơ
A
B
→
là A.
A
B
→
1
;
-
1
;
1
B.
A
B
→...
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho các điểm A(-1;2;-3); B(2; -1; 0). Tọa độ của vectơ A B → là
A. A B → = 1 ; - 1 ; 1
B. A B → = 1 ; 1 ; - 3
C. A B → = 3 ; - 3 ; 3
D. A B → = 3 ; - 3 ; - 3