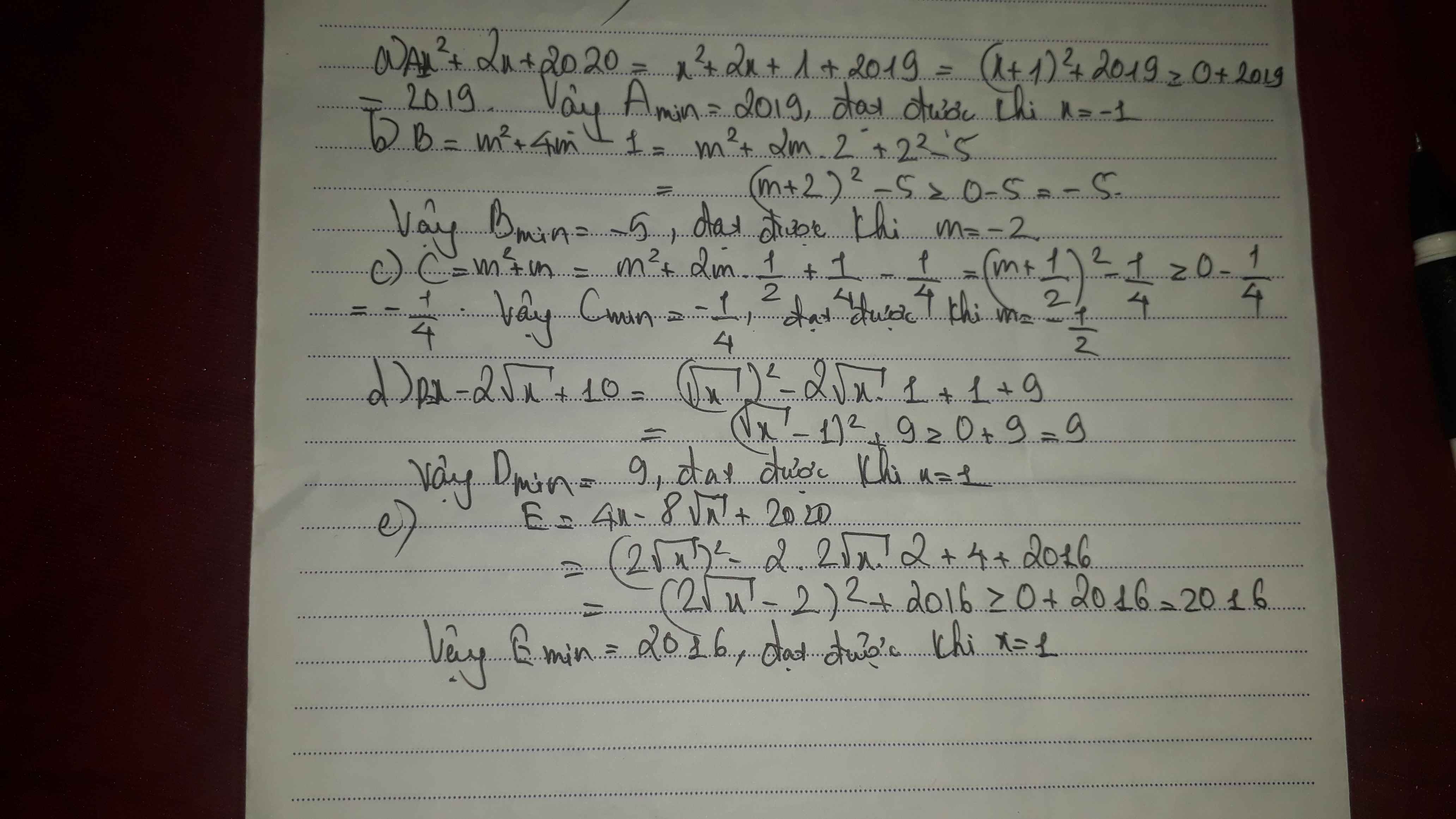\(P=4x^2+4x+1-2\left|2x+1\right|+2019\)

\(P=\left|2x+1\right|^2-2\left|2x+1\right|+1+2018\)

\(P=\left(\left|2x+1\right|-1\right)^2+2018\ge2018\)

\(\Rightarrow P_{min}=2018\) khi \(\left|2x+1\right|-1=0\Rightarrow\left[{}\begin{matrix}2x+1=1\\2x+1=-1\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=0\\x=-1\end{matrix}\right.\)

\(B=\frac{\left(x-2\right)^2+2016}{\left(x-1\right)^2}=\frac{\left(t-1\right)^2+2016}{t^2}=\frac{t^2-2t+2017}{t^2}\)

\(=1-\frac{2}{t}+\frac{2017}{t^2}=1-2a+2017a^2=2017\left(a^2-2.\frac{1}{4034}+\frac{1}{4034}^2\right)-\frac{2017}{4034^2}+1\)

\(=2017\left(a-\frac{1}{4034}\right)^2+1-\frac{1}{2017^3}\ge1-\frac{1}{2017^3}\)

tự xét dấu = 

\(B=\frac{\left(x-2\right)^2+2016}{\left(x-1\right)^2}\)

\(\Leftrightarrow\frac{\left(t-1\right)^2+2016}{1^2}\)

\(\Leftrightarrow\frac{t^2-2t+2017}{t^2}\)

\(\Leftrightarrow1-\frac{2}{t}+\frac{2017}{t^2}\)

\(\Leftrightarrow1-2a+2017a^2\)

\(\Leftrightarrow a^2-2\times[\frac{1}{4034}+\frac{1^2}{4034}]-\frac{2017}{4034^2}+1\)

\(\Leftrightarrow2017\left(a-\frac{1}{4034}\right)^2+1-\frac{1}{2017}^3\)

phần cuối tự làm nha

toi ko bt

có ai làm NY tui hem

a.

\(A=\dfrac{2013}{x^2}-\dfrac{2}{x}+1=2013\left(\dfrac{1}{x}-\dfrac{1}{2013}\right)^2+\dfrac{2012}{2013}\ge\dfrac{2012}{2013}\)

Dấu "=" xảy ra khi \(x=2013\)

b.

\(B=\dfrac{4x^2+2-4x^2+4x-1}{4x^2+2}=1-\dfrac{\left(2x-1\right)^2}{4x^2+2}\le1\)

\(B_{max}=1\) khi \(x=\dfrac{1}{2}\)

\(B=\dfrac{-2x^2-1+2x^2+4x+2}{4x^2+2}=-\dfrac{1}{2}+\dfrac{\left(x+1\right)^2}{2x^2+1}\ge-\dfrac{1}{2}\)

\(B_{max}=-\dfrac{1}{2}\) khi \(x=-1\)

\(a,=x^2+2x+1+2019=\left(x+1\right)^2+2019\ge2019\) dấu"=" xảy ra<=>x=-1

b,\(=m^2+2.2m+4-5=\left(m+2\right)^2-5\ge-5\) dấu"=" xảy ra<=>m=-2

c, \(=x-2\sqrt{x}+10=x-2\sqrt{x}+1+9=\left(\sqrt{x}-1\right)^2+9\ge9\)

dấu"=" xảy ra<=>x=1

b, \(4x-8\sqrt{x}+2020=4x-2.2.2\sqrt{x}+4+2016=\left(2\sqrt{x}-2\right)^2+2016\ge2016\)

dấu"=" xảy ra<=>x=1

a) Ta có: \(x^2+2x+2020\)

\(=x^2+2x+1+2019\)

\(=\left(x+1\right)^2+2019\ge2019\forall x\)

Dấu '=' xảy ra khi x=-1

b) Ta có: \(m^2+4m-1\)

\(=m^2+4m+4-5\)

\(=\left(m+2\right)^2-5\ge-5\forall m\)

Dấu '=' xảy ra khi m=-2

c) Ta có: \(m^2+m\)

\(=m^2+2\cdot m\cdot\dfrac{1}{2}+\dfrac{1}{4}-\dfrac{1}{4}\)

\(=\left(m+\dfrac{1}{2}\right)^2-\dfrac{1}{4}\ge-\dfrac{1}{4}\forall m\)

Dấu '=' xảy ra khi \(m=-\dfrac{1}{2}\)

Ta có

A=2x²+4y²-4x+4xy+2020

=(x^2+4y^2+4xy)+(x^2-4x+4)+2016

=(x+2y)^2+(x-2)^2+2016

Thấy

(x+2y)^2>=0 với mọi x,y

(x-2)^2>=0 với mọi x

=>(x+2y)^2+(x-2)^2+2016>=2016 với mọi x,y

Hay Min A>=2016

Dấu "=" xảy ra<=>(x+2y)^2=0 và(x-2)^2=0

<=>x=2;y=-1

Vậy Min A=2016 tại x=2 và y=-1