cho đoạn thẳng CD , 2 điểm A và B không thuộc C,D sao cho AC=AD , BC=BD chứng minh AB vuông góc CD

Những câu hỏi liên quan
cho đoạn thẳng AB và CD a)Chứng minh nếu AB vuông góc với CD thì AC^2 -BC^ = AD^2 - BD^2 b) Chứng minh ngược lại với câu a, có AC^2 -BC^ = AD^2 - BD^2 thì AB vuông góc với CD Sài định lí 4 điểm nha mọi người!
cho đoạn thẳng AB và CD a)Chứng minh nếu AB vuông góc với CD thì AC^2 -BC^ = AD^2 - BD^2 b) Chứng minh ngược lại với câu a, có AC^2 -BC^ = AD^2 - BD^2 thì AB vuông góc với CD Sài định lí 4 điểm nha mọi người!
Mình cần gấp!
Gọi giao của AB và CD là O
a: AB vuông góc CD
AC^2-BC^2
=AO^2+OC^2-CO^2-BO^2
=AO^2-BO^2
=AO^2+OD^2-OD^2-OB^2
=AD^2-BD^2
b: AC^2-BC^2=AD^2-BD^2
=>AC^2-AD^2=BC^2-BD^2
=>(vecto AC)^2-(vecto AD)^2=(vecto BC)^2-(vecto BD)^2
=>(vecto AC-vecto AD)(vecto AC+vecto AD)=(vecto BC-vecto BD)(vecto BC+vecto BD)
=>vecto DC*vecto AM*2=vecto DC*vecto BM*2(M là trung điểm của DC)
=>vecto DC*vecto AB=0
=>DC vuông góc AB
Đúng 1
Bình luận (2)
Bài 2: cho đoạn thẳng AB; vẽ cung tròn tâm (A;AB) , và cung tròn (B;AB) cắt nhau ở C và Da/ -Chứng minh tam giác ABC tam giác ABD -tam giác ACD tam giác BCDb/AB có là tia phân giác của CAD không ? vì sao? Bài 3:cho góc xOy nhọn; Om là phân giác của góc xOy; C thuộc Om lấy A thuộc Ox ; B thuộc Oy sao cho OA OB - chứng minh : a/ BCCA góc OCB Góc COA và góc OBC góc OAC Bài 4 : cho AB cắt CD trung điểm I của chúng (ABCD)- Chứng minh...
Đọc tiếp
Bài 2: cho đoạn thẳng AB; vẽ cung tròn tâm (A;AB) , và cung tròn (B;AB) cắt nhau ở C và D
a/ -Chứng minh tam giác ABC= tam giác ABD
-tam giác ACD= tam giác BCD
b/AB có là tia phân giác của CAD không ? vì sao?
Bài 3:cho góc xOy nhọn; Om là phân giác của góc xOy; C thuộc Om lấy A thuộc Ox ; B thuộc Oy sao cho OA = OB
- chứng minh : a/ BC=CA
góc OCB= Góc COA
và góc OBC= góc OAC
Bài 4 : cho AB cắt CD trung điểm I của chúng (AB>CD)
- Chứng minh a/ AC=BC; AD=BC
b/ AC// BD; AD//BC
Bài 2:
Nối C với D ta được đoạn thẳng CD
Nối C với B, B với D, D với A, A với C, A với B ( Nói chung là gần giống vs hình của hoàng thị ngọc anh)
a)Xét tam giác ABC và tam giác ABD có:
AB chung
BC=AC (cùng cung tròn tâm A và B, bán kính AB)(gọi giải thích này là(1))
BD=AD (như trên)
-> 2 tam giác này bằng nhau(2)
b)Xét tam giác ACD và tam giác BCD có:
CD chung
AC=BC (1)
AD=BD (1)
-> 2 tam giác này bằng nhau
c) vì tam giác ABC bằng tam giác ABD (2)
-> góc CAB bằng góc BAD (2 góc tương ứng)
vậy AB là tpg của góc A
Đúng 0
Bình luận (0)
a) Vì AC thuộc đường tròn (A;AB)
AD thuộc đg tròn (A;AB)
=> AC = AD
Tượng tự: BC thuộc đg tròn (B;AB)
BD thuộc đg tròn (B;AB)
=> BC = BD
Xét tg ABC và tg ABD có:
AC = AD ( c/m trên)
AB cạnh chung( GT)
BC = BD ( c/m trên)
=> ΔABC = ΔABD ( c.c.c)→ ĐPCM
Ttự: AC ϵ (A; AB)
BC ϵ (B; AB). Do 2 đg tròn có bán kính bằng nhau
=> AC = BC
TT: AD = BD
Xét ΔACD và ΔBCD có:
AC = BC (c/m trên)
CD cạnh chung
AD = BD ( c/m trên)
=> ΔACD = ΔBCD(c.c.c)→ ĐPCM
Đúng 0
Bình luận (2)
Đó là hình vẽ bài 2 thôi, để mk nghĩ đã nha!
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Bài 2: cho đoạn thẳng AB; vẽ cung tròn tâm (A;AB) , và cung tròn (B;AB) cắt nhau ở C và Da/ -Chứng minh tam giác ABC tam giác ABD-tam giác ACD tam giác BCDb/AB có là tia phân giác của CAD không ? vì sao?Bài 3:cho góc xOy nhọn; Om là phân giác của góc xOy; C thuộc Om lấy A thuộc Ox ; B thuộc Oy sao cho OA OB- chứng minh : a/ BCCAgóc OCB Góc COAvà góc OBC góc OACBài 4 : cho AB cắt CD trung điểm I của chúng (ABCD)- Chứng minh a/ ACBC; ADBCb/ AC// BD; AD//BC
Đọc tiếp
Bài 2: cho đoạn thẳng AB; vẽ cung tròn tâm (A;AB) , và cung tròn (B;AB) cắt nhau ở C và D
a/ -Chứng minh tam giác ABC= tam giác ABD
-tam giác ACD= tam giác BCD
b/AB có là tia phân giác của CAD không ? vì sao?
Bài 3:cho góc xOy nhọn; Om là phân giác của góc xOy; C thuộc Om lấy A thuộc Ox ; B thuộc Oy sao cho OA = OB
- chứng minh : a/ BC=CA
góc OCB= Góc COA
và góc OBC= góc OAC
Bài 4 : cho AB cắt CD trung điểm I của chúng (AB>CD)
- Chứng minh a/ AC=BC; AD=BC
b/ AC// BD; AD//BC
1.Cho tam giác ABC có ABAC ;tia phân giác của góc BAC cắt BC tại D .C hứng minh rằng AD là đường trung trực của đoạn thẳng BC2.Cho tam giác ABC.Đường thẳng qua A và song song với AB ở D. Chứng minh rằng AB CD ;BCAD3. Cho tam giác ABC vuongở A .Gọi M là trung điểm của cạnh AC,D là điểm trên nửa mặt phẳng bờ là AC không chứa B sao cho góc MCD90độ và CDAB.Chứng minh M là trung điểmcủa đoạn thẳng BD
Đọc tiếp
1.Cho tam giác ABC có AB=AC ;tia phân giác của góc BAC cắt BC tại D .C hứng minh rằng AD là đường trung trực của đoạn thẳng BC
2.Cho tam giác ABC.Đường thẳng qua A và song song với AB ở D. Chứng minh rằng AB= CD ;BC=AD
3. Cho tam giác ABC vuongở A .Gọi M là trung điểm của cạnh AC,D là điểm trên nửa mặt phẳng bờ là AC không chứa B sao cho góc MCD=90độ và CD=AB.Chứng minh M là trung điểmcủa đoạn thẳng BD
Cho tam giác ABC vuông tại A có
B
^
55
°
. Trên nửa mặt phẳng bờ AC không chứa B, vẽ tia Cx vuông góc với AC. Trên tia Cx lấy điểm D sao cho CD AB.a) Tính số đo
A
C
B
^
b) Chứng minh
∆
A
B
C
∆
C
D
A
và AD//BC.c) Kẻ
A
H
⊥
B
C
(...
Đọc tiếp
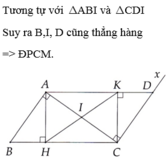
Cho tam giác ABC vuông tại A có B ^ = 55 ° . Trên nửa mặt phẳng bờ AC không chứa B, vẽ tia Cx vuông góc với AC. Trên tia Cx lấy điểm D sao cho CD = AB.
a) Tính số đo A C B ^
b) Chứng minh ∆ A B C = ∆ C D A và AD//BC.
c) Kẻ A H ⊥ B C ( H ∈ B C ) và C K ⊥ A D ( K ∈ A D ) . Chứng minh BH = DK.
d) Gọi I là trung điểm của AC. Chứng minh ba điểm H, I, K thẳng hàng và 3 đường thẳng AC, HK, BD cùng gặp nhau ở I.
Cho tam giác ABC vuông tại A. Vẽ đường phân giác CD ( D AB). Lấy điểm M BC sao cho
CA = CM.
a) Chứng minh : .
b) Chứng minh : CD là đường trung trực của đoạn thẳng AM và AD < DB.
c) Vẽ AH vuông góc với BC tại H, lấy N thuộc BC sao cho BN = BA. Gọi O là giao điểm của AN và CD. Chứng minh O cách đều ba cạnh của tam giác AHC.
Cho tam giác ABC vuông tại A có 0 B 55 . Trên nửa mặt phẳng bờ AC không chứa B, vẽ tia Cx vuông góc với AC. Trên tia Cx lấy điểm D sao cho CD = AB a) Tính số đo góc ACB b) Chứng minh ABC CDA và AD // BC c) Kẻ AH BC( H BC) và CK AD ( K AD). Chứng minh BH = DK d) Gọi I là trung điểm của AC. Chứng minh ba điểm H,I,K thẳng hàng và 3 đường thẳng AC,HK,BD cùng gặp nhau ở I
Cho tam giác ABC cân tại A có góc B = góc C bằng 40 độ. Kẻ phân giác BD ( D thuộc AC). Trên tia AB lấy điểm M sao cho AM = BC. Từ D dựng đường thẳng song song với BC cắt AB tại E.
a) Chứng minh DE = CD
b) Chứng minh BD + AD = BC
c) tính góc AMC