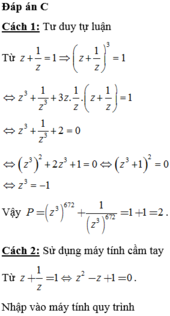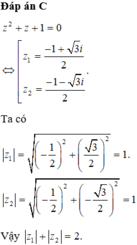Gọi z1 và z2 là nghiệm của phương trình z+1/z=-1. Gía trị của P=z2016+(1/z2016)+\(\frac{ }{ }\)
Những câu hỏi liên quan
Cho biểu thức L 1- z+ z2- z3+ ...+ z2016- z2017 với . Biểu thức L có giá trị là A. 1 - i. B. 1 + i.
Đọc tiếp
Cho biểu thức L = 1- z+ z2- z3+ ...+ z2016- z2017 với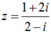 
. Biểu thức L có giá trị là
A. 1 - i.
B. 1 + i.
Chọn A.
+ Ta có:
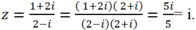
+ Khi đó: L = 1- z+ z2- z3+ ...+ z2016- z2017
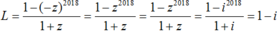
Đúng 0
Bình luận (0)
Biết số phức z thỏa mãn phương trình z + 1 z = 1 . Tính giá trị biểu thức P = z 2016 + 1 z 2016
A. 0
B. 1
C. 2
D. 3
Biết số phức z thỏa mãn phương trình z + 1 z = 1 . Tính giá trị biểu thức P = z 2016 + 1 z 2016
A. P=0
B. P=1
C. P=2
D. P=3
Đáp án C
Cách 1: Tư duy tự luận
Từ
z + 1 z = 1 ⇒ z + 1 z 3 = 1 ⇔ z 3 + 1 z 3 + 3 z . 1 z . z + 1 z = 1 ⇔ z 3 + 1 z 3 + 2 = 0
⇔ z 3 2 + 2 z 3 + 1 = 0 ⇔ z 3 + 1 2 = 0 ⇔ z 3 = − 1
Vậy P = z 3 672 + 1 z 3 672 = 1 + 1 = 2 .
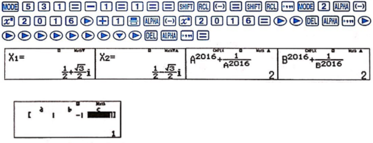
Cách 2: Sử dụng máy tính cầm tay
Từ z + 1 z = 1 ⇔ z 2 − z + 1 = 0 . Nhập vào máy tính quy trình
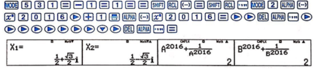
Đúng 0
Bình luận (0)
Gọi z1 và z2 là hai nghiệm phức của phương trình z2-4z+5=0 trong đó z1 có phần ảo dương .Gía trị của biểu thức (z1-1)2021+(z2-1)2022 bằng
Lời giải:
Theo đề thì $z_1=2+i, z_2=2-i$. Khi đó:
$A=(z_1-1)^{2021}+(z_2-1)^{2022}=(i+1)^{2021}+(1-i)^{2022}$
Ta có:
$(i+1)^2=i^2+1+2i=(-1)+1+2i$
$(1-i)^2=1+i^2-2i=-2i$
$\Rightarrow A=(2i)^{1010}(i+1)+(-2i)^{1011}$
$=2^{1010}.(i^2)^{505}(i+1)+(-2)^{1011}.(i^2)^{505}.i$
$=2^{1010}.(-1)^{505}(i+1)+(-2)^{1011}.(-1)^{505}i$
$=-(i+1).2^{1010}+2^{1011}i$
$=2^{1010}(i-1)$
Đúng 1
Bình luận (0)
Gọi
z
1
,
z
2
là hai nghiệm phức của phương trình
z
2
+
z
+
1
0
.
Giá trị của biểu thức
z
1
+
z
2
bằng A.
1
2
B. 4 C. 2 D. 1
Đọc tiếp
Gọi z 1 , z 2 là hai nghiệm phức của phương trình z 2 + z + 1 = 0 . Giá trị của biểu thức z 1 + z 2 bằng
A. 1 2
B. 4
C. 2
D. 1
Gọi
z
1
và
z
2
là hai nghiệm phức của phương trình
z
2
+
z
+
1
0
. Tính giá trị của
z
1
2017
+...
Đọc tiếp
Gọi z 1 và z 2 là hai nghiệm phức của phương trình z 2 + z + 1 = 0 . Tính giá trị của z 1 2017 + z 2 2017
A. 
B. 
C. 
D. 
Đáp án C
Phương pháp: Tính z 1 , z 2 và sử dụng công thức Moivre
Cách giải: Phương trình z 2 + z + 1 có ∆ = 1 - 4 = - 3 nên có 2 nghiệm
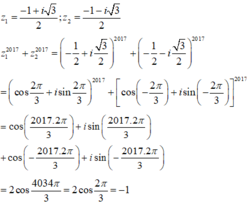
Đúng 0
Bình luận (0)
Gọi
z
1
và
z
2
là hai nghiệm phức của phương trình
z
2
+
z
+
1
0
. Tính giá trị của
z
1
2017
+
z
2
2017
A.
z
1
2017
+
z...
Đọc tiếp
Gọi z 1 và z 2 là hai nghiệm phức của phương trình z 2 + z + 1 = 0 . Tính giá trị của z 1 2017 + z 2 2017
A. z 1 2017 + z 2 2017 = 1
B. z 1 2017 + z 2 2017 = 2
C. z 1 2017 + z 2 2017 = -1
D. z 1 2017 + z 2 2017 = -2
Gọi z1, z2 lần lượt là hai nghiệm của phương trình z2 - (1 + 3i) z – 2 + 2i = 0 và thỏa mãn | z1| > | z2|. Tìm giá trị của biểu thức
A. 0,5
B. 1,5
C. 1
D. 2
Chọn B.
Phương trình đã cho tương đương với:
( z – 2i) ( z – 1 – i) = 0
Suy ra: z = 2i hoặc z = 1 + i
Do | z1| > | z2|. nên ta có z1 = 2i và z2 = 1 + i
Ta có
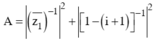
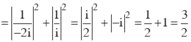
Đúng 0
Bình luận (0)
Trong tập các số phức gọi
z
1
,
z
2
là hai nghiệm của phương trình
z
2
-
z
+
2017
4
với
z
2
có phần ảo dương. Cho số phức z thỏa mãn |z-
z
1
| 1 Giá trị nhỏ nhất của P |z...
Đọc tiếp
Trong tập các số phức gọi z 1 , z 2 là hai nghiệm của phương trình z 2 - z + 2017 4 với z 2 có phần ảo dương. Cho số phức z thỏa mãn |z- z 1 | = 1 Giá trị nhỏ nhất của P = |z- z 2 | là
A . 2016 - 1
B . 2017 - 1
C . 2017 - 1 2
D . 2016 - 1 2
Đáp án A
Phương trình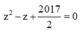 
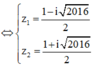
Ta có 
Vật giá trị nhỏ nhất của biểu thức P là 
Đúng 0
Bình luận (0)
Trong tập các số phức, gọi
z
1
,
z
2
là hai nghiệm của phương trình
z
2
-
z
+
2017
4
0
với ...
Đọc tiếp
Trong tập các số phức, gọi z 1 , z 2 là hai nghiệm của phương trình z 2 - z + 2017 4 = 0 với z 2 có thành phần ảo dương. Cho số phức z thỏa mãn z - z 1 = 1 . Giá trị nhỏ nhất của P = z - z 2 là
A. 2016 - 1
B. 2017 - 1 2
C. 2016 - 1 2
D. 2017 - 1
Đáp án A
Phương pháp.
Giả sử 
Giả phương trình ban đầu để tìm được nghiệm
z
1
,
z
2
Sử dụng giả thiết để đánh giá cho cho b. Đưa 
về một hàm cho b và sử dụng ước lượng cho b ở phần trước để tìm giá trị nhỏ nhất của P.
Lời giải chi tiết.
Tính toán ta tìm được hai nghiệm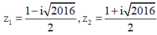 
Giả sử 
. Từ 
ta suy ra
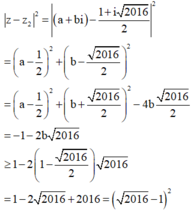
Áp dụng (1) ta nhận được
Do đó giá trị nhỏ nhất của 
là
2016
-
1
Đạt được khi và chỉ khi 
Đúng 0
Bình luận (0)