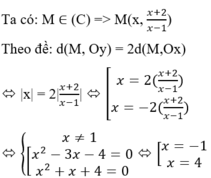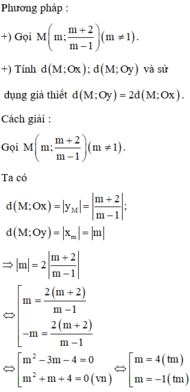Cho hàm số \(y=x^2\) có đồ thị là (P) và đường thẳng (d) : y = x +2
1. Tìm các điểm thuộc Parabol có khoảng cách đến trục tung gấp 2 lần khoảng cách đến trục hoành
2. Tìm tập hợp các điểm M . Từ M kẻ được hai đường thẳng vuông góc với nhau và tiếp xúc với Parabol