 Làm hộ mik câu 2 3 vs
Làm hộ mik câu 2 3 vs

Những câu hỏi liên quan
làm từ câu 6 hộ mik vs:))
1) Xét ΔAMB và ΔAMC có
AB=AC(ΔBAC cân tại A)
AM chung
BM=CM(M là trung điểm của BC)
Do đó: ΔAMB=ΔAMC(c-c-c)
Suy ra: \(\widehat{AMB}=\widehat{AMC}\)(hai góc tương ứng)
mà \(\widehat{AMB}+\widehat{AMC}=180^0\)(hai góc kề bù)
nên \(\widehat{AMB}=\widehat{AMC}=\dfrac{180^0}{2}=90^0\)
hay AM\(\perp\)BC
Ta có: ΔAMB=ΔAMC(cmt)
nên \(\widehat{BAM}=\widehat{CAM}\)(hai góc tương ứng)
hay AM là tia phân giác của \(\widehat{BAC}\)(đpcm)
3) Xét ΔABC có
H là trung điểm của AB(gt)
K là trung điểm của AC(gt)
Do đó: HK là đường trung bình của ΔABC(Định nghĩa đường trung bình của tam giác)
Suy ra: HK//BC(Định lí 2 về đường trung bình của tam giác)
Đúng 0
Bình luận (0)
Các bạn làm hộ mik câu này vs
https://olm.vn/hoi-dap/question/1283084.html
Làm hộ mik bài 2 câu b) và cả bài 3 ạ,mik cảm ơn
 làm hộ mik bài 2 vs ạ
làm hộ mik bài 2 vs ạ

làm hộ mik câu 3 ( mik đang cần gấp ạ )
\(A=\dfrac{2\sqrt{x}+17}{\sqrt{x+5}}=\dfrac{2\sqrt{x}+10}{\sqrt{x}+5}+\dfrac{7}{\sqrt{x}+5}=2+\dfrac{7}{\sqrt{x}+5}\)
Để \(A\) ∈ \(Z\) thì \(\dfrac{7}{\sqrt{x}+5}\) phải ∈ \(Z\)
=> \(\sqrt{x}+5\) ∈ \(Ư\left(7\right)=\left\{-7;-1;1;7\right\}\)
# Với \(\sqrt{x}+5=-7=>\sqrt{x}=-12\)(Loại)
#Với \(\sqrt{x}+5=-1=>\sqrt{x}=-6\)(Loại)
#Với \(\sqrt{x}+5=1=>\sqrt{x}=-4\left(Loại\right)\)
#Với \(\sqrt{x}+5=7=>\sqrt{x}=2< =>x=4\left(Nhận\right)\)
Vậy \(x=4\) thì \(A\)∈\(Z\)
Đúng 0
Bình luận (0)
\(\sqrt[3]{\dfrac{a^4}{b^2\left(a^2-ab+b^2\right)}}+\sqrt[3]{\dfrac{b^4}{c^2\left(b^2-bc+c^2\right)}}\sqrt[3]{\dfrac{c^4}{a^2\left(c^2-ac+b^2\right)}}\) \(\text{≥}3\)
\(Ta\) \(Có\) : \(\sqrt[3]{\dfrac{a^4}{b^2\left(a^2-ab+b^2\right)}}=\sqrt[3]{\dfrac{a^6}{ab.ab\left(a^2-ab+b^2\right)}}=\dfrac{a^2}{\sqrt[3]{ab.ab.\left(a^2-ab+b^2\right)}}\)
\(Áp\) \(dụng\) \(bđt\) \(AM-GM\)
\(\sqrt[3]{ab.ab\left(a^2-ab+b^2\right)}\text{≤}\) \(\dfrac{ab+ab+a^2-ab+b^2}{3}\)
\(=>\dfrac{a^2}{\sqrt[3]{ab.ab\left(a^2-ab+b^2\right)}}\) \(\text{≥}\) \(\dfrac{3a^2}{a^2+ab+b^2}\) \(Hay\) \(\sqrt[3]{\dfrac{a^4}{b^2\left(a^2-ab+b^2\right)}}\text{≥}\dfrac{3a^2}{a^2+ab+b^2}\)
Tương tự ta cũng có :
\(\sqrt[3]{\dfrac{b^4}{c^2\left(b^2-bc+c^2\right)}}\text{≥}\dfrac{3b^2}{b^2+bc+c^2}\)
\(\sqrt[3]{\dfrac{c^4}{a^2\left(c^2-ac+a^2\right)}}\text{≥}\dfrac{3c^2}{a^2+ac+c^2}\)
\(=>\text{}\text{}\)\(\sqrt[3]{\dfrac{a^4}{b^2\left(a^2-ab+b^2\right)}}+\sqrt[3]{\dfrac{b^4}{c^2\left(b^2-bc+c^2\right)}}\sqrt[3]{\dfrac{c^4}{a^2\left(c^2-ac+b^2\right)}}\) \(\text{≥}\) \(3\left(\dfrac{a^2}{a^2+ab+b^2}+\dfrac{b^2}{b^2+bc+c^2}+\dfrac{c^2}{a^2+ac+c^2}\right)\)
Cần c/m \(\left(\dfrac{a^2}{a^2+ab+b^2}+\dfrac{b^2}{b^2+bc+c^2}+\dfrac{c^2}{a^2+ac+c^2}\right)\) ≥ \(1\)
Ta có : \(\dfrac{a^2}{a^2+ab+b^2}\text{≥}\dfrac{1}{3}\)
\(< =>3a^2\text{≥}a^2+ab+b^2\) \(< =>2a^2-b\left(a+b\right)\text{≥}0\) (1)
Lại có : \(a^2\text{≥}-b\left(a+b\right)\) (2)
Từ (1) và (2) => \(\dfrac{a^2}{a^2+ab+b^2}\text{≥}\dfrac{1}{3}\)
Tương tự ta cũng có :
\(\dfrac{b^2}{b^2+bc+c^2}\text{≥}\dfrac{1}{3}\)
\(\dfrac{c^2}{a^2+ac+c^2}\text{≥}\dfrac{1}{3}\)
Do đó \(\dfrac{a^2}{a^2+ab+b^2}+\dfrac{b^2}{b^2+bc+c^2}+\dfrac{c^2}{a^2+ac+c^2}\text{≥}1\)
Suy ra : \(\sqrt[3]{\dfrac{a^4}{b^2\left(a^2-ab+b^2\right)}}+\sqrt[3]{\dfrac{b^4}{c^2\left(b^2-bc+c^2\right)}}\sqrt[3]{\dfrac{c^4}{a^2\left(c^2-ac+b^2\right)}}\) \(\text{≥}\) \(3\)
Đẳng thức xảy ra <=> \(a=b=c=1\)
Đúng 0
Bình luận (0)
làm hộ minh câu 3 và câu 4 vs ạ
Làm hộ mik vs
Làm hộ mk câu D bài 3 vs ạ 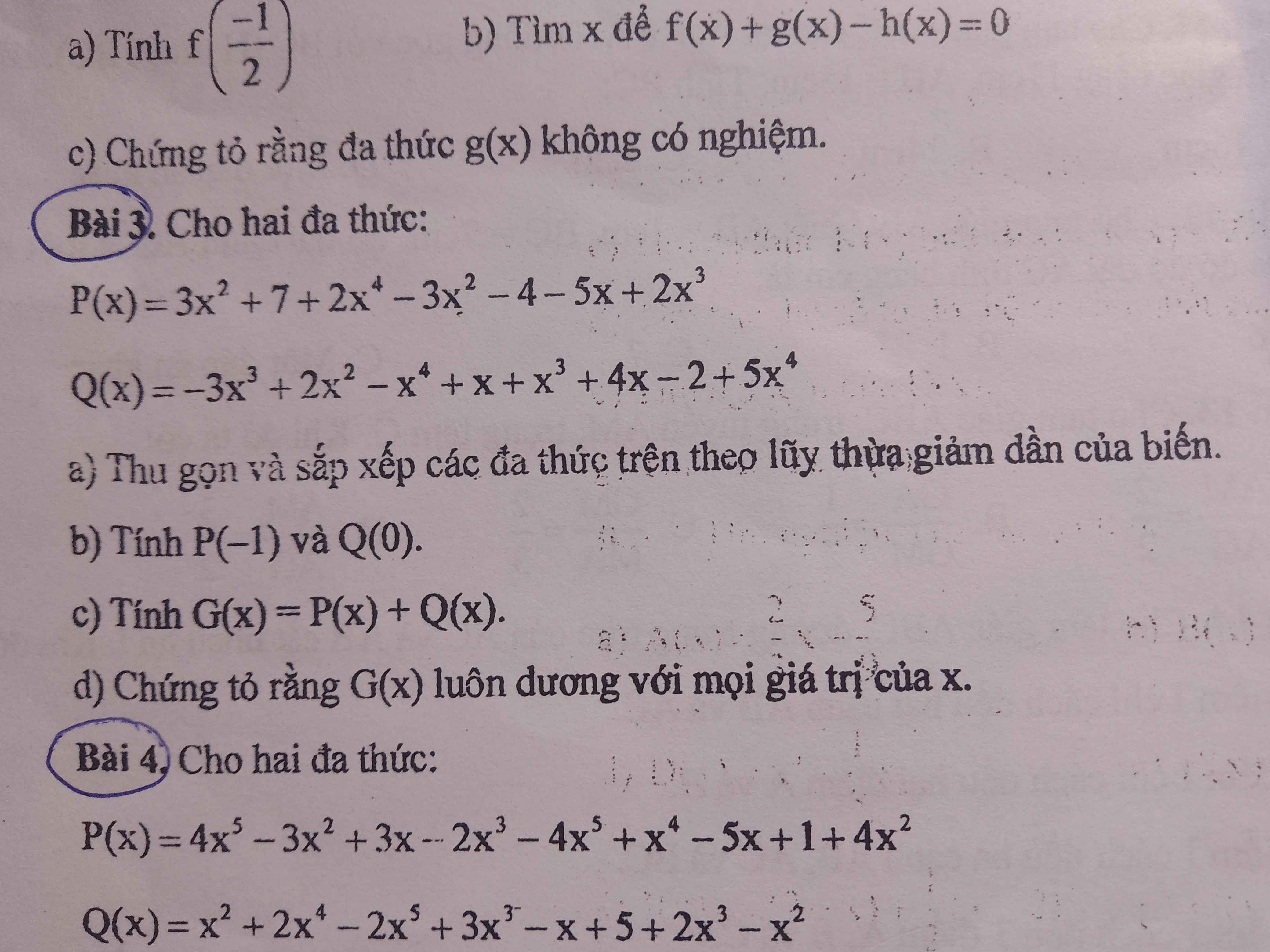
3:
a: \(P\left(x\right)=2x^4+2x^3-5x+3\)
\(Q\left(x\right)=4x^4-2x^3+2x^2+5x-2\)
b: P(-1)=2-2-3+5+3=5
Q(0)=4*0-2*0+2*0+5*0-2=-2
c: G(x)=2x^4+2x^3-5x+3+4x^4-2x^3+2x^2+5x-2
=6x^4+2x^2+1
d: G(x)=x^2(6x^2+2)+1>0 với mọi x
Đúng 0
Bình luận (0)
Làm hộ mik vs ạ:((
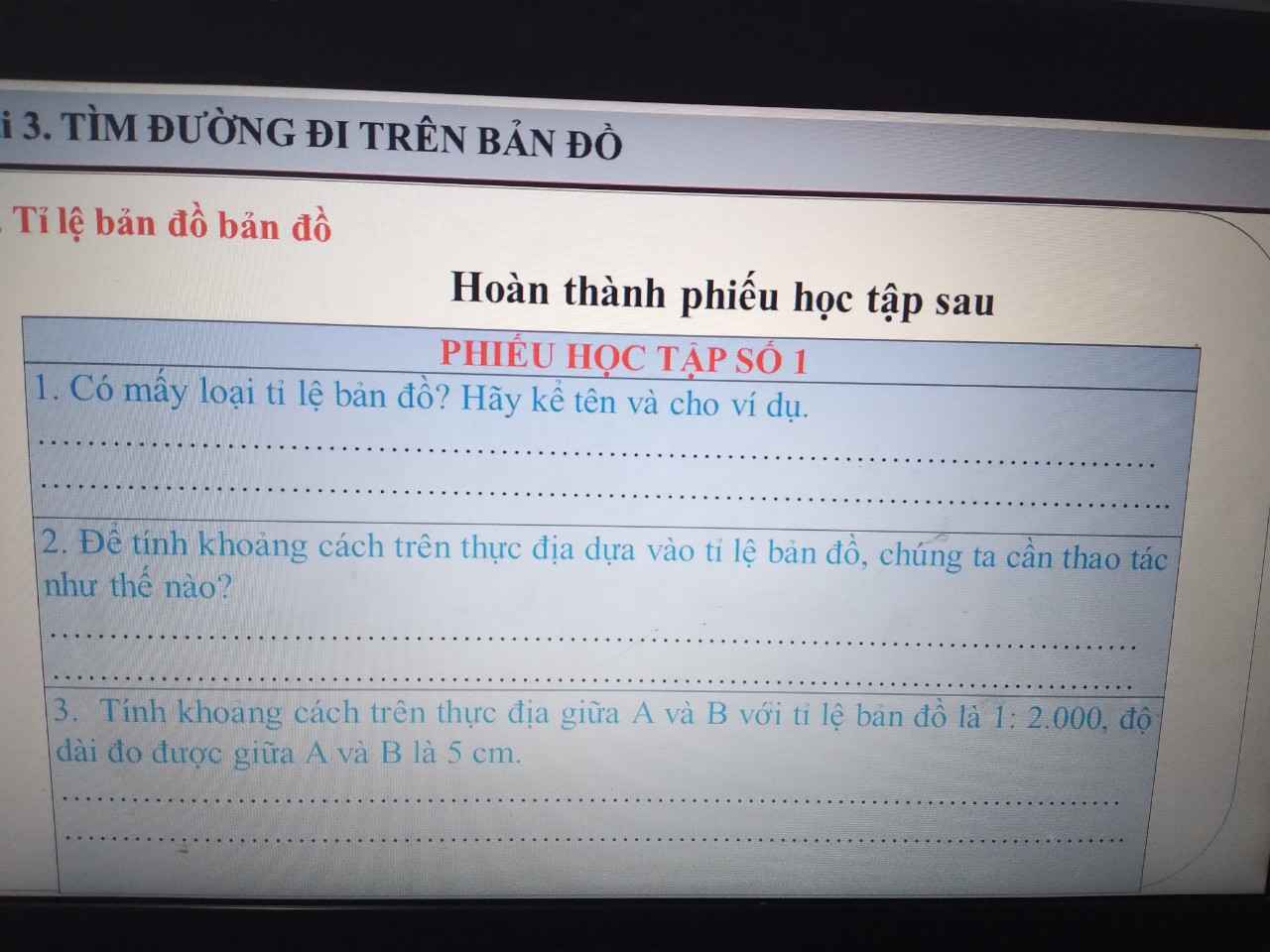
Câu 1:
Có hai loại tỉ lệ bản đồ:
-Tỉ lệ số: Là 1 phân số luôn có tử số là 1,mẫu số càng lớn thì tỉ lệ càng nhỏ và ngược lại.
-Tỉ lệ thước:là tỉ lệ được vẽ dưới dạng 1 thước đo đã tính sẵn,mỗi đoạn đều có 1 độ dài tương ứng.
Đúng 0
Bình luận (0)













