Hình bạn tự vẽ nha.

a)   Xét tam giác ADB và tam giác AEC có:

            góc BAC là góc chung

            góc ADB =góc AEC

   Suy ra: Tam giác ADB đồng dạng với tam giác AEC (g.g)

    => AD/AE = AB/AC (cạnh tương ứng)

   => AD/AB = AE/AC 

Xét tam giác AED và tam giác ACB có:

    góc BAC là góc chung

    AD/AB = AE/AC (cmt)

Suy ra tam giác AED đồng dạng với tam giác ACB (c.g.c)

b) Gọi giao điểm của AH và BC là K.

Xét tam giác ABC có

BD và CE là 2 đường cao mà chúng cắt nhau tại H

nên H là trực tâm của tam giác ABC

=>AK vuông góc với BC

 Xét tam giác BKH và tam giác BDC có:

   góc HBK là góc chung

   góc BKH = góc BDC

Suy ra BD/BK = BC/BH

=> BD.BH = BC.BK (1)

Chứng minh tương tự ta cũng có : tam giác CKH đồng dạng với tam giác CEB

=> CK/CE = CH/CB 

=> CE.CH = BC.CK  (2)

Lấy (1)+(2) ta được đpcm

Xét tam giác BAD, ta có:

CosA= \(\dfrac{AD}{AB}\) (1)

Xét tam giác CAE, ta có:

CosA= \(\dfrac{AE}{AC}\) (2)

Từ (1) và (2) suy ra:

\(\dfrac{AD}{AB}=\dfrac{AE}{AC}\) (3)

Ta lại có: góc A : góc chung (4)

Từ (3) và (4) suy ra:

Tam giác ADE ∽ tam giác ABC

a) Xét ΔEHB vuông tại E và ΔDHC vuông tại D có

\(\widehat{EHB}=\widehat{DHC}\)(hai góc đối đỉnh)

Do đó: ΔEHB∼ΔDHC(góc nhọn)

b) Ta có: ΔEHB∼ΔDHC(cmt)

\(\Leftrightarrow\frac{HE}{HD}=\frac{HB}{HC}\)(hai cặp cạnh tương ứng tỉ lệ)

hay \(\frac{HE}{HB}=\frac{HD}{HC}\)

Xét ΔHED và ΔHBC có

\(\frac{HE}{HB}=\frac{HD}{HC}\)(cmt)

\(\widehat{EHD}=\widehat{BHC}\)(hai góc đối đỉnh)

Do đó: ΔHED∼ΔHBC(c-g-c)

c) Xét ΔADB vuông tại D và ΔAEC vuông tại E có

\(\widehat{DAB}\) chung

Do đó: ΔADB∼ΔAEC(g-g)

\(\Leftrightarrow\frac{AD}{AE}=\frac{AB}{AC}\)(hai cặp cạnh tương ứng tỉ lệ)

hay \(\frac{AD}{AB}=\frac{AE}{AC}\)

Xét ΔADE và ΔABC có

\(\frac{AD}{AB}=\frac{AE}{AC}\)(cmt)

\(\widehat{DAE}\) chung

Do đó: ΔADE∼ΔABC(c-g-c)

d) Gọi K là giao điểm của AH và BC

Xét ΔABC có

BD là đường cao ứng với cạnh AC(gt)

CE là đường cao ứng với cạnh AB(gt)

BD\(\cap\)CE={H}

Do đó: H là trực tâm của ΔABC(Định lí ba đường cao của tam giác)

⇔AH⊥BC

⇔AK⊥BC(AH\(\cap\)BC={K})

Xét ΔBKH vuông tại K và ΔBDC vuông tại D có

\(\widehat{DBC}\) chung

Do đó: ΔBKH∼ΔBDC(góc nhọn)

\(\Leftrightarrow\frac{BK}{BD}=\frac{BH}{BC}\)(hai cặp cạnh tương ứng tỉ lệ)

hay \(BK\cdot BC=BH\cdot BD\)

Xét ΔCKH vuông tại K và ΔCEB vuông tại E có

\(\widehat{ECB}\) chung

Do đó: ΔCKH∼ΔCEB(g-g)

\(\Leftrightarrow\frac{CK}{CE}=\frac{CH}{CB}\)(hai cặp cạnh tương ứng tỉ lệ)

hay \(CK\cdot CB=CE\cdot CH\)

Ta có: \(BD\cdot BH+CE\cdot CH=BK\cdot BC+CK\cdot BC\)

\(=BC\cdot\left(BK+CK\right)=BC\cdot BC=BC^2\)(đpcm)

Hình tự vẽ nha:))

a) Xét ΔEHB và ΔDHC có:

∠BEH=∠CDH=90^o

∠EHB=∠DHC(đối đỉnh)

Do đó, ΔEHB∼ΔDHC (gg).

b) Xét ΔHED và HBC có:

\(\frac{HE}{HB}=\frac{HD}{HC}\)(ΔEHB∼ΔDHC)

∠DHE=∠BHC (đđ)

Do đó,ΔHED∼ΔHBC(cgc)

c) Xét ΔADB và ΔAEC có:

∠A chung

∠ADB=∠AEC=90^o

Do đó, ΔADB∼ΔAEC(gg)

Xét ΔAED và ΔABC có:

∠A chung

\(\frac{AD}{AB}=\frac{AE}{AC}\)(ΔADB∼ΔAEC)

Do đó, ΔAED∼ΔABC(cgc)

d) Vẽ HK⊥BC(K∈BC)

ΔBHK∼ΔBDC(gg)⇒\(\frac{BK}{BD}=\frac{BH}{BC}\)⇔BK.BC=BH.BD

ΔCHK∼ΔCBE(gg)⇒\(\frac{CK}{CE}=\frac{CH}{CB}\)⇔CK.BC=CE.CH

⇒BC(BK+CK)=BH.BD+CE.CH

⇔BC²=BH.BD+CE.CH (đpcm)

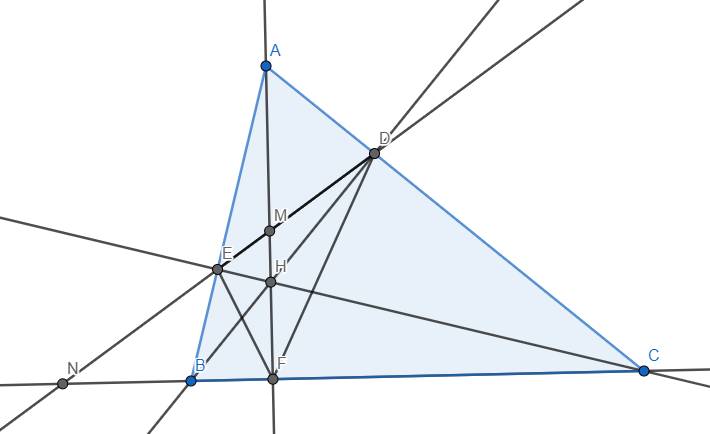
a) Xét \(\Delta ABD\) và \(\Delta ACE\), ta có \(\widehat{ADB}=\widehat{AEC}\left(=90^o\right)\) và góc A chung \(\Rightarrow\Delta ABD~\Delta ACE\left(g.g\right)\) \(\Rightarrow\dfrac{AB}{AC}=\dfrac{AD}{AE}\) \(\Rightarrowđpcm\)

b) Từ \(AE.AB=AD.AC\Rightarrow\dfrac{AD}{AB}=\dfrac{AE}{AC}\)

Xét \(\Delta ADE\) và \(\Delta ABC\), ta có \(\dfrac{AD}{AB}=\dfrac{AE}{AC}\) và góc A chung \(\Rightarrowđpcm\)

c) Do \(\Delta ADE~\Delta ABC\) \(\Rightarrow\dfrac{S_{ADE}}{S_{ABC}}=\left(\dfrac{AD}{AB}\right)^2\)

Lại có \(\dfrac{AD}{AB}=cosA=cos45^o=\dfrac{1}{\sqrt{2}}\) nên \(\dfrac{S_{ADE}}{S_{ABC}}=\left(\dfrac{1}{\sqrt{2}}\right)^2=\dfrac{1}{2}\)\(\Rightarrow\dfrac{S_{ADE}}{S_{ABC}-S_{ADE}}=\dfrac{1}{2-1}\) \(\Rightarrow\dfrac{S_{ADE}}{S_{BEDC}}=1\)

d) Kẻ đường cao AF của tam giác ABC. Tương tự câu b, ta chứng minh được các tam giác BFE và CDF cùng đồng dạng với tam giác ABC. Từ đó suy ra \(\Delta BEF~\Delta DCF\) \(\Rightarrow\widehat{BFE}=\widehat{CFD}\) \(\Rightarrow90^o-\widehat{BFE}=90^o-\widehat{CFD}\) \(\Rightarrow\widehat{EFM}=\widehat{DFM}\) \(\Rightarrow\) FM là tia phân giác trong tam giác DEF \(\Rightarrow\dfrac{MD}{ME}=\dfrac{FD}{FE}\).

Mặt khác, \(FN\perp FM\) \(\Rightarrow\) FN là phân giác ngoài của tam giác DEF \(\Rightarrow\dfrac{ND}{NE}=\dfrac{FD}{FE}\). Từ đó suy ra \(\dfrac{MD}{ME}=\dfrac{ND}{NE}\) \(\Rightarrowđpcm\)

Bài làm:

a) Δ EHB ~ Δ DHC (g.g) vì:

+ \(\widehat{EHB}=\widehat{DHC}\) (đối đỉnh)

+ \(\widehat{BEH}=\widehat{CDH}=90^0\)

=> đpcm

b) Theo phần a, 2 tam giác đồng dạng

=> \(\frac{HE}{HB}=\frac{HD}{HC}\)

Δ HED ~ Δ HBC (c.g.c) vì:

+ \(\frac{HE}{HB}=\frac{HD}{HC}\) (chứng minh trên)

+ \(\widehat{EHD}=\widehat{BHC}\) (đối đỉnh)

=> đpcm

c) Δ ABD ~ Δ ACE (g.g) vì:

+ \(\widehat{ADB}=\widehat{AEC}=90^0\)

+ \(\widehat{A}\) chung

=> \(\frac{AD}{AE}=\frac{AB}{AC}\)

Δ ADE ~ Δ ABC (c.g.c) vì:

+ \(\frac{AD}{AE}=\frac{AB}{AC}\) (chứng minh trên)

+ \(\widehat{A}\) chung

=> đpcm

d) Gọi F là giao của AH với BC

Δ BHF ~ Δ BCD (g.g) vì:

+ \(\widehat{BFH}=\widehat{BDC}=90^0\)

+ \(\widehat{B}\) chung

=> \(\frac{BF}{BH}=\frac{BD}{BC}\Rightarrow BD.BH=BF.BC\left(1\right)\)

Tương tự ta chứng minh được:

\(CH.CE=FC.BC\left(2\right)\)

Cộng vế (1) và (2) lại ta được:

\(BD.BH+CH.CE=\left(BF+FC\right)BC=BC.BC=BC^2\)

=> đpcm