Giải phương trình:
a) x4 + 8x3+ 15x2 - 4x -2 = 0
Những câu hỏi liên quan
Giải phương trình x4 – 8x3 + 21x2 -24x + 9 = 0
Ta có: \(x^4-8x^3+21x^2-24x+9=0\)
\(\Leftrightarrow x^4-5x^3+3x^2-3x^3+15x^2-9x+3x^2-5x+9=0\)
\(\Leftrightarrow\left(x^2-5x+3\right)\left(x^2-3x+3\right)=0\)
\(\Leftrightarrow x^2-5x+3=0\)
\(\text{Δ}=\left(-5\right)^2-4\cdot1\cdot3=25-12=13\)
Vì Δ>0 nên phương trình có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}x_1=\dfrac{5-\sqrt{13}}{2}\\x_2=\dfrac{5+\sqrt{13}}{2}\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Không giải phương trình, hãy cho biết mỗi phương trình sau có bao nhiêu nghiệm?
a
)
15
x
2
+
4
x
−
2005
0
b
)
−
19
5...
Đọc tiếp
Không giải phương trình, hãy cho biết mỗi phương trình sau có bao nhiêu nghiệm?
a ) 15 x 2 + 4 x − 2005 = 0 b ) − 19 5 x 2 − 7 x + 1890 = 0
a) Phương trình 15 x 2 + 4 x – 2005 = 0 có a = 15; c = -2005 trái dấu
⇒ Phương trình có hai nghiệm phân biệt.
b) Phương trình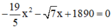 
có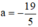 
; c = 1890 trái dấu
⇒ Phương trình có hai nghiệm phân biệt.
Đúng 0
Bình luận (0)
Giải các phương trình sau:a)
x
+
2
3
+
x
+
1
3
0
;
b)
2
x
4
+
3
x
2
−
5
0
;
c)
x...
Đọc tiếp
Giải các phương trình sau:
a) x + 2 3 + x + 1 3 = 0 ;
b) 2 x 4 + 3 x 2 − 5 = 0 ;
c) x 4 − 8 x 3 − 9 x 2 = 0 ;
d) x 3 − 4 x 2 + 4 − x = 0 .
Không giải phương trình, hãy cho biết mỗi phương trình sau có bao nhiêu nghiệm?
15 x 2 + 4 x - 2005 = 0
Phương trình 15x2 + 4x – 2005 = 0 có a = 15; c = -2005 trái dấu
⇒ Phương trình có hai nghiệm phân biệt.
Đúng 0
Bình luận (0)
Giải bất phương trình
1
5
x
2
-
4
x
1
A. x4 B. x0 C. 0x4 D.
∀
x
∈
ℝ
Đọc tiếp
Giải bất phương trình 1 5 x 2 - 4 x > 1
A. x>4
B. x<0
C. 0<x<4
D. ∀ x ∈ ℝ
Tìm tất cả các giá trị của tham số m để phương trình
9
.
9
x
2
-
2
x
–
(
2
m
+
1
)
15
x
2
-
2
x
+
1
+...
Đọc tiếp
Tìm tất cả các giá trị của tham số m để phương trình 9 . 9 x 2 - 2 x – ( 2 m + 1 ) 15 x 2 - 2 x + 1 + 4 m - 2 5 2 x 2 - 4 x + 2 = 0 có 2 nghiệm thực phân biệt
A. 1 2 < m < 1
B. m > 3 + 6 2 hoặc m < 3 - 6 2
C. m > 1 hoặc m < 1 2
D. 3 - 6 2 < m < 3 + 6 2
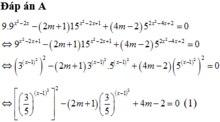
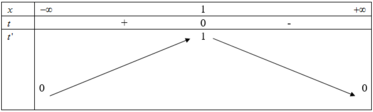
Dựa vào bảng biến thiên hàm f(x), ta thấy để phương trình (1) có 2 nghiệm thực x phân biệt thì phương trình (2) phải có duy nhất 1 nghiệm thuộc khoảng (0;1), nghiệm còn lại (nếu có) khác 1. Số nghiệm của (2) là số giao điểm của đồ thị hàm số y = 3 5 x - 1 2 và đường thẳng y = 2 m - 1 nên điều kiện của m thỏa mãn là 0 < 2 m - 1 < 1 ⇔ 1 2 < m < 1
Đúng 0
Bình luận (0)
giải phương trình sau:
a. (9x2-4)(x+1) = (3x+2) (x2-1)
b. (x-1)2-1+x2 = (1-x)(x+3)
c. (x2-1)(x+2)(x-3) = (x-1)(x2-4)(x+5)
d. x4+x3+x+1=0
e. x3-7x+6 = 0
f. x4-4x3+12x-9 = 0
g. x5-5x3+4x = 0
h. x4-4x3+3x2+4x-4 = 0
m.n jup vs
giải bất phương trình:
1)(2x+1)(x-3)(1-5x)<0
2)x^4>8x
3)(x-2)(x+3)<=0
4)(4x+3)(x-1)<(x-1)^2
3: =>x+3>=0 và x-2<=0
=>-3<=x<=2
4: =>4x^2-4x+3x-3<x^2-2x+1
=>3x^2+x-2<0
=>3x^2+3x-2x-2<0
=>(x+1)(3x-2)<0
=>-1<x<2/3
2: =>x^4-8x>0
=>x(x^3-8)>0
=>x>2 hoặc x<0
Đúng 0
Bình luận (0)
Giả sử x1, x2 là hai nghiệm của phương trình: x2 – x + A = 0 và x3, x4 là hai nghiệm của phương trình: x2 – 4x + B = 0. Tính A, B biết rằng x1, x2, x3, x4 lập thành một cấp số nhân tăng?
1) Cho phương trình x 4 + m x 2 - m - 1 = 0(m là tham số)
a) Giải phương trình khi m = 2
1) x 4 + m x 2 - m - 1 = 0
a) Khi m = 2, phương trình trở thành: x 4 + 2 x 2 – 3 = 0
Đặt x 2 = t (t ≥ 0). Khi đó ta có phương trình: t 2 + 2t - 3 = 0
⇒ Phương trình có nghiệm t = 1 và t = -3 (do phương trình có dạng a + b + c = 0)
Do t ≥ 0 nên t = 1 ⇒ x 2 = 1 ⇒ x = ±1
Đúng 0
Bình luận (0)