a.

Ta có: \(\left\{{}\begin{matrix}-4a=-2\\8b=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=2\\b=-4\end{matrix}\right.\) \(\Rightarrow I\left(2;-4\right)\)

\(R=\sqrt{2^2+\left(-4\right)^2+5}=5\)

b.

PTTT: \(\left(C\right):\left(a-x_0\right)\left(x-x_0\right)+\left(b-y_0\right)\left(y-y_0\right)=0\)

\(\Leftrightarrow\left(2+1\right)\left(x+1\right)+\left(-4-0\right)\left(y-0\right)=0\)

\(\Leftrightarrow\left(C\right):3x-4y=-3\)

c.

Ta có: \(\Delta\perp d\Rightarrow\Delta:4x+3y+c=0\)

\(d\left(I,\Delta\right):\dfrac{\left|4\cdot2-3\cdot4+c\right|}{\sqrt{4^2+3^2}}=5\)

\(\Leftrightarrow\left|c-4\right|=25\) \(\Leftrightarrow\left[{}\begin{matrix}c=29\\c=-21\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}\Delta:4x+3y+29=0\\\Delta:4x+3y-21=0\end{matrix}\right.\)

Do tiếp tuyến hợp với trục hoành 1 góc 45 độ

\(\Rightarrow\) Tiếp tuyến có hệ số góc k thỏa mãn: \(\left|k\right|=tan45^0=1\Rightarrow k=\pm1\)

\(\Rightarrow\) Phương trình tiếp tuyến có dạng: \(\left[{}\begin{matrix}x-y+c=0\\x+y+c_1=0\end{matrix}\right.\)

Đường tròn (C) tâm \(I\left(2;-2\right)\) bán kính \(R=3\)

\(\Rightarrow d\left(I;d\right)=R\Rightarrow\left[{}\begin{matrix}\dfrac{\left|2-\left(-2\right)+c\right|}{\sqrt{1^2+\left(-1\right)^2}}=3\\\dfrac{\left|2+\left(-2\right)+c_1\right|}{\sqrt{1^2+1^2}}=3\end{matrix}\right.\)

\(\Rightarrow\left[{}\begin{matrix}c=-4+3\sqrt{2}\\c=-4-3\sqrt{2}\\c_1=3\sqrt{2}\\c_1=-3\sqrt{2}\end{matrix}\right.\)

Có 4 tiếp tuyến thỏa mãn:

\(\left[{}\begin{matrix}x-y-4+3\sqrt{2}=0\\x-y-4-3\sqrt{2}=0\\x+y+3\sqrt{2}=0\\x+y-3\sqrt{2}=0\end{matrix}\right.\)

cho (C) : x2 + y2 - 4x + 4y - 1 = 0, viết phương trình tiếp tuyến d hợp với trục hoành một góc 45 độ. - Hoc24

a: (C): x^2-4x+4+y^2+6y+9=25

=>(x-2)^2+(y+3)^2=25

=>R=5; I(2;-3)

\(IM=\sqrt{\left(5-2\right)^2+\left(1+3\right)^2}=5\)

=>M thuộc (C)

vecto IM=(3;4)

Phương trình tiếp tuyến tại M là:

3(x-2)+4(y+3)=0

=>3x-6+4y+12=0

=>3x+4y+6=0

b: (d)//-3x+4y+3=0

=>(d): -3x+4y+c=0; I(2;-3)

d(I;(d))=5

=>\(\dfrac{\left|2\cdot\left(-3\right)+4\cdot\left(-3\right)+c\right|}{\sqrt{\left(-3\right)^2+4^2}}=5\)

=>|c-18|=25

=>c=43 hoặc c=-7

c: (d) vuông góc (-3x+4y+3)=0

=>(d): 4x+3y+c=0

I(2;-3)

\(d\left(I;\left(d\right)\right)=5\)

=>\(\dfrac{\left|2\cdot4+\left(-3\right)\cdot3+c\right|}{5}=5\)

=>|c-1|=25

=>c=26 hoặc c=-24

Lời giải:

Tiếp tuyến $(d')$ cần tìm song song với $(d): x+y-3=0$ nên có dạng $x+y+m=0$

Viết lại PTĐTr $(C): (x-1)^2+(y+2)^2=8$

$\Rightarrow$ tâm $I(1;-2)$ và bán kính $R=2\sqrt{2}$

Vì $(d')$ là tiếp tuyến của $(C)$ nên: \(d(I, d')=R\Leftrightarrow \frac{|x_I+y_I+m|}{\sqrt{1^2+1^2}}=2\sqrt{2}\)

\(\Leftrightarrow |m-1|=4\Rightarrow m=5\) hoặc $m=-3$. TH $m=-3$ loại do trùng với $(d)$

Vậy PTTT cần tìm là $x+y+5=0$

a) x2 + y2 – 4x + 8y – 5 = 0

⇔ (x2 – 4x + 4) + (y2 + 8y + 16) = 25

⇔ (x – 2)2 + (y + 4)2 = 25.

Vậy (C) có tâm I(2 ; –4), bán kính R = 5.

b) Thay tọa độ điểm A vào phương trình đường tròn ta thấy:

(–1 – 2)2 + (0 + 4)2 = 32 + 42 = 52= R2

⇒ A thuộc đường tròn (C)

⇒ tiếp tuyến (d’) cần tìm tiếp xúc với (C) tại A

⇒ (d’) là đường thẳng đi qua A và vuông góc với IA

⇒ (d’) nhận 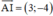 là một vtpt và đi qua A(–1; 0)

⇒ phương trình (d’): 3(x + 1) – 4(y - 0)= 0 hay 3x – 4y + 3 = 0.

c) Gọi tiếp tuyến vuông góc với (d) : 3x – 4y + 5 = 0 cần tìm là (Δ).

(d) có 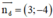 là một vtpt; 1 VTCP là ud→(4; 3)

(Δ) ⊥ (d) ⇒ (Δ) nhận 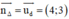 là một vtpt

⇒ (Δ): 4x + 3y + c = 0.

(C) tiếp xúc với (Δ) ⇒ d(I; Δ) = R

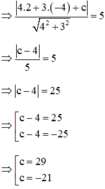
Vậy (Δ) : 4x + 3y + 29 = 0 hoặc 4x + 3y – 21 = 0.

a: (C): x^2-4x+4+y^2+6y+9=25

=>(x-2)^2+(y+3)^2=25

=>R=5; I(2;-3)

\(IM=\sqrt{\left(5-2\right)^2+\left(1+3\right)^2}=5\)

=>M thuộc (C)

vecto IM=(3;4)

Phương trình tiếp tuyến tại M là:

3(x-2)+4(y+3)=0

=>3x-6+4y+12=0

=>3x+4y+6=0

b: (d)//-3x+4y+3=0

=>(d): -3x+4y+c=0; I(2;-3)

d(I;(d))=5

=>\(\dfrac{\left|2\cdot\left(-3\right)+4\cdot\left(-3\right)+c\right|}{\sqrt{\left(-3\right)^2+4^2}}=5\)

=>|c-18|=25

=>c=43 hoặc c=-7

c: (d) vuông góc (-3x+4y+3)=0

=>(d): 4x+3y+c=0

I(2;-3)

\(d\left(I;\left(d\right)\right)=5\)

=>\(\dfrac{\left|2\cdot4+\left(-3\right)\cdot3+c\right|}{5}=5\)

=>|c-1|=25

=>c=26 hoặc c=-24