giải bất phương trình
(16-x2)/(√x2-9x+8) lớn hơn hoặc bằng 0
Giải bất phương trình g ' ( x ) ≤ 0 với g ( x ) = x 2 + 3 x − 9 x − 2
A. S = (1; 3)
B. S = 1 ; 3 / 2
C. S = − ∞ ; 1 ∪ ( 3 ; + ∞ )
D. S = − ∞ ; 1
Ta có
g ' ( x ) = ( 2 x + 3 ) . ( x − 2 ) − 1. ( x 2 + 3 x − 9 ) ( x − 2 ) 2 = x 2 − 4 x + 3 ( x − 2 ) 2
Mà g ' ( x ) ≤ 0
⇔ x 2 − 4 x + 3 ≤ 0 x − 2 ≠ 0 ⇔ 1 ≤ x ≤ 3 x ≠ 2 ⇔ x ∈ 1 ; 3 \ 2
Vậy tập nghiệm bất phương trình là: S=[1 ; 3]\{2}
Chọn đáp án B
Giải các bất phương trình sau:
a) 2 - x >= (lớn hơn hoặc bằng) 0
b) 2 + x >= (lớn hơn hoặc bằng) 0
c) 7 - x >= (lớn hơn hoặc bằng) 0
Giúp mình với nhé, thanks
a) \(2-x\ge0\Leftrightarrow x\le2\)(chuyển x sang bên phải rồi đảo vế)
b) \(2+x\ge0\Leftrightarrow x\ge-2\)(cộng cả hai vế với -2)
c) \(7-x\ge0\Leftrightarrow x\le7\)(giống phần a)
Bạn tự kết luận nha!!
1/ Giải bất phương trình
a) x2>4
b) x2<9
c) (x-1)2>hoặc= 4
d) (1-2x)2<hoặc= 0,09
e) x2+6x-7>0
f) x2-x<2
g) 4x2-12x<hoặc=\(\dfrac{-135}{16}\)
`a)x^2>4`
`<=>sqrtx^2>sqrt4`
`<=>|x|>2`
`<=>` \(\left[ \begin{array}{l}x>2\\x<-2\end{array} \right.\)
`b)x^2<9`
`<=>\sqrtx^2<sqrt9`
`<=>|x|<3`
`<=>-3<x<3`
`c)(x-1)^2>=4`
`<=>\sqrt{(x-1)^2}>=sqrt4`
`<=>|x-1|>=2`
`<=>` \(\left[ \begin{array}{l}x-1 \ge 2\\x-1 \le -2\end{array} \right.\)
`<=>` \(\left[ \begin{array}{l}x \ge 3\\x \le -1\end{array} \right.\)
`d)(1-2x)^2<=0,09`
`<=>\sqrt{(1-2x)^2}<=sqrt{0,09}`
`<=>|2x-1|<=0,3`
`<=>-0,3<=2x-1<=0,3`
`<=>0,7<=2x<=1,3`
`<=>0,35<=x<=0,65`
`e)x^2+6x-7>0`
`<=>x^2-x+7x-7>0`
`<=>x(x-1)+7(x-1)>0`
`<=>(x-1)(x+7)>0`
TH1:
\(\left[ \begin{array}{l}x-1>0\\x+7>0\end{array} \right.\)
`<=>` \(\left[ \begin{array}{l}x>1\\x>-7\end{array} \right.\)
`<=>x>1`
TH2"
\(\left[ \begin{array}{l}x-1<0\\x+7<0\end{array} \right.\)
`<=>` \(\left[ \begin{array}{l}x<1\\x<-7\end{array} \right.\)
`<=>x<-7`
`f)x^2-x<2`
`<=>x^2-x-2<0`
`<=>x^2-2x+x-2<0`
`<=>x(x-2)+x-2<0`
`<=>(x-2)(x+1)<0`
`<=>` \(\begin{cases}x-2<0\\x+1>0\\\end{cases}\)
`<=>` \(\begin{cases}x<2\\x>-1\\\end{cases}\)
`<=>-1<x<2`
a) x2 > 4
<=> \(\left[{}\begin{matrix}x>2\\x< -2\end{matrix}\right.\)
b) \(x^2< 9\)
<=> \(-3< x< 3\)
c) \(\left(x-1\right)^2\ge4\)
<=> \(\left[{}\begin{matrix}x-1\ge2< =>x\ge3\\x-1\le-2< =>x\le-1\end{matrix}\right.\)
d) \(\left(1-2x\right)^2\le0,09\)
<=> \(-0,3\le1-2x\le0,3\)
<=> \(1,3\ge2x\ge0,7\)
<=> \(0,65\ge x\ge0,35\)
e) \(x^2+6x-7>0\)
<=> \(\left(x+7\right)\left(x-1\right)>0\)
<=> \(\left[{}\begin{matrix}x-1>0< =>x>1\\x+7< 0< =>x< -7\end{matrix}\right.\)
f) \(x^2-x< 2\)
<=> \(x^2-x-2< 0\)
<=> \(\left(x-2\right)\left(x+1\right)< 0\)
<=> \(\left\{{}\begin{matrix}x+1>0< =>x>-1\\x-2< 0< =>x< 2\end{matrix}\right.\)
<=> -1 < x < 2
g) \(4x^2-12x\le\dfrac{-135}{16}\)
<=> \(64x^2-192x+135\le0\)
<=> (8x - 15)(8x - 9) \(\le0\)
<=> \(\left\{{}\begin{matrix}8x-15\le0< =>x\le\dfrac{15}{8}\\8x-9\ge0< =>x\ge\dfrac{9}{8}\end{matrix}\right.\)
<=> \(\dfrac{9}{8}\le x\le\dfrac{15}{8}\)
Giải bất phương trình :
x 2 - 1 x 2 - 3 - 3 x 2 + 2 x + 8 > 0
A. S = - 3 ; - 4 3 ∪ ( - 1 ; 1 )
B. S = - 3 ; - 4 3 ∪ 3 ; 2
C. ![]()
D. 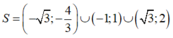
Chọn D
Lập bảng xét dấu
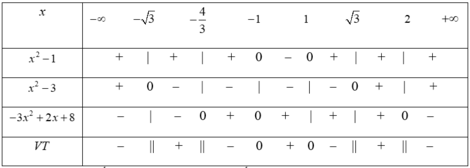
Dựa vào bảng xét dấu, ta có tập nghiệm của bất phương trình đã cho là:
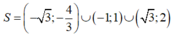
cho pt: \(x^3-x^2+2mx-2m=0\left(1\right)\)
a, Tìm m để phương trình có ba nghiệm phân biệt x1,x2,x3 tm: x1+x2+x3=10
b,Tìm m để phương trình có ba nghiệm phân biệt đều lớn hơn hoặc bằng 1.
\(x^3-x^2+2mx-2m=0\)
\(\Leftrightarrow x^2\left(x-1\right)+2m\left(x-1\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x^2+2m\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x^2=-2m\end{matrix}\right.\)
Để pt có 3 nghiệm \(\Rightarrow-2m>0\Rightarrow m< 0\)
a. Do vai trò 3 nghiệm như nhau, ko mất tính tổng quát giả sử \(x_1=1\) và \(x_2;x_3\) là nghiệm của \(x^2+2m=0\)
Để pt có 3 nghiệm pb \(\Rightarrow\left\{{}\begin{matrix}-2m>0\\-2m\ne1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}m< 0\\m\ne-\dfrac{1}{2}\end{matrix}\right.\)
Khi đó: \(x_2+x_3=0\Rightarrow x_1+x_2+x_3=1\ne10\) với mọi m
\(\Rightarrow\) Không tồn tại m thỏa mãn yêu cầu
b.
Giả sử pt có 3 nghiệm, khi đó \(\left[{}\begin{matrix}x_2=-\sqrt{-2m}< 0< 1\\x_3=\sqrt{-2m}\end{matrix}\right.\)
\(\Rightarrow\) Luôn có 1 nghiệm của pt âm \(\Rightarrow\) không tồn tại m thỏa mãn
Em coi lại đề bài
Giải bất phương trình sau
(x+2)(x2-2x+4)-x(x2+2)> hoặc = 5
=>x^3+8-x^3-2x>=5
=>-2x>=-3
=>x<=3/2
Trong các phương trình sau, những bất phương trình nào tương đương với −2x−1<−9 ?
A. x2 -16<0 C.2x+3>11
B. x>4 D. x2 -16>0
Trong các phương trình sau, những bất phương trình nào tương đương với −2x−1<−9 ?
A. x2 -16<0 C.2x+3>11
B. x>4 D. x2 -16>0
GIẢI BẤT PHƯƠNG TRÌNH
10x2 + 11x + 3 " lớn hơn hoặc bằng " 0
\(10x^2+11x+3\ge0\)
\(\Leftrightarrow10x^2+5x+6x+3\ge0\)
\(\Leftrightarrow5x\left(2x+1\right)+3\left(2x+1\right)\ge0\)
\(\Leftrightarrow\left(5x+3\right)\left(2x+1\right)\ge0\)
\(\Rightarrow x\le-\frac{3}{5};-\frac{1}{2}\le x\)
Giải các bất phương trình sau
a) (x2+2)2-(x+2)(x-2)(x2+4)-4x(x+1)< hoặc = 20
b) (x+2)(x2-2x+4)-x(x2+2)> hoặc = 15
a) \(\left(x^2+2\right)^2-\left(x+2\right)\left(x-2\right)\left(x^2+4\right)-4x\left(x+1\right)\le20\)
\(\Leftrightarrow x^4+4x^2+4-x^4+16-4x^2-4x\le20\)
\(\Leftrightarrow\left(x^4-x^4\right)+\left(4x^2-4x^2\right)-4x+4+16\le20\)
\(\Leftrightarrow-4x+20\le20\)
\(\Leftrightarrow-4x\le20-20\)
\(\Leftrightarrow-4x\le0\)
\(\Leftrightarrow-4x:-4\ge0:-4\)
\(\Leftrightarrow x\ge0\)
Vậy nghiệm của bất phương trình là: \(x\ge0\)
b) \(\left(x+2\right)\left(x^2-2x+4\right)-x\left(x^2+2\right)\ge15\)
\(\Leftrightarrow x^3+8-x^3-2x\ge15\)
\(\Leftrightarrow\left(x^3-x^3\right)+8-2x\ge15\)
\(\Leftrightarrow8-2x\ge15\)
\(\Leftrightarrow-2x\ge15-8\)
\(\Leftrightarrow-2x\ge7\)
\(\Leftrightarrow-2x:-2\le7:-2\)
\(\Leftrightarrow x\le-\dfrac{7}{2}\)
Vậy nghiệm của bất phương trình là \(x\le-\dfrac{7}{2}\)
a: =>x^4+4x^2+4-x^4+16-4x^2-4x<=20
=>-4x+20<=20
=>-4x<=0
=>x>=0
b: =>x^3+8-x^3-2x>=15
=>-2x>=7
=>x<=-7/2