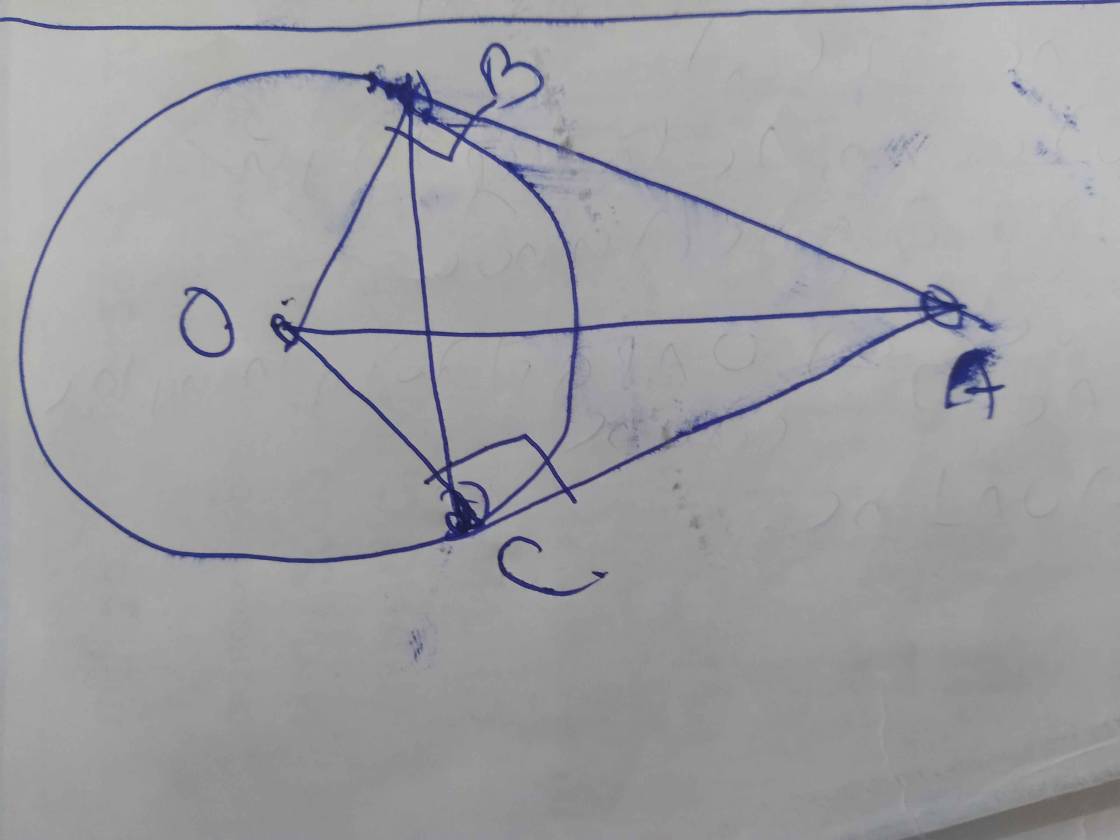
cho OA = 2 OF chứng minh A 'B ' bằng AB

Những câu hỏi liên quan
Bài 2
Cho góc xOy = 90 độ, A thuộc Ox, B thuộc Oy. Lấy E trên tia Oa đối của tia Ox; F trên tia Oy sao cho OE = OB; OF = OA
A) Chứng Minh : AB = EF : AB vuông góc EF
B) GỌI M; N là trung điểm của AB; EF. Chứng minh OM = ON
Bài 2
Cho góc xOy = 90 độ, A thuộc Ox, B thuộc Oy. Lấy E trên tia Oa đối của tia Ox; F trên tia Oy sao cho OE = OB; OF = OA
A) Chứng Minh : AB = EF : AB vuông góc EF
B) GỌI M; N là trung điểm của AB; EF. Chứng minh OM = ON
HELP ME
Trên tia OX vẽ 2 điểm A và b sao cho OA bằng 4cm OB bằng 6cm a]điểm A có nằm giữa O và B ko .Vì sao b] so sánh OA và AB c, gọi x là trung điểm của OA .chứng minh A là trung điểm của đoạn thẳng YB
Giải:a) Điểm A nằm giữa O và B vì OA < OB (4cm < 6cm)
b) Do A nằm giữa O và B nên OA + AB = OB
=> AB = OB - OA = 6 - 4 = 2 (cm)
=> OA > AB (4cm > 2cm)
c) Xem lại để, sửa lại: Gọi Y là trung điểm ..... YB
Do Y là trung điểm của OA nên OY = YA = OA/2 = 4/2 = 2 (cm)
=> YA = AB = 2 cm
Mà A nằm giữa Y và B
=> A là trung điểm của đt YB
Cho (O) và một điểm A ở ngoài đường tròn, từ A kẻ 2 tiếp tuyến AB,AC ( B và C là hai tiếp điểm ) a, Cho OA=13cm, OB=5cm. Tính AB,AC b, Chứng minh OA là tia phân giác của góc BOC c, Chứng minh OA vuông góc với BC
Cho tam giác a b c d e là các điểm sao cho AC bằng 2 lần ab OD = 1/2 OB bằng 1/3 OA Chứng minh rằng C D E thẳng hàng
Cho góc xOy hai điểm A, B thứ tự chuyển động trên Ox, Oy đường tròn nội tiếp tam giác OAB tiếp xúc với OA, OB ở E,F
a, Chứng minh răng OE = OF = ( OA + OB - AB ) /2
b, Nếu chu vi tam giác OAB không đổi chứng minh AB luôn tiếp xúc với đường tròn cố định
Cho góc vuông xOy, điểm A trên tia Ox, điểm B trên tia Oy. Lấy điểm E trên tia đối của tia Ox, điểm F trên tia Oy sao cho OE = OB, OF = OA.
a) Chứng minh AB = EF, AB \(\perp\) EF.
b) Gọi M, N lần lượt là trung điểm của AB và EF. Chứng minh rằng tam giác OMN vuông cân.
Cho góc xOy bằng 60 độ. Trên Ox lấy điểm A, trên Oy lấy điểm B sao cho OA= OB. Kẻ OH vuông góc với AB( H thuộc AB)
a) chứng minh OH là đường trung trực của đoạn thẳng AB
b)Chứng minh tam giác OAB đều
c) chứng minh tam giác OHA bằng tam giác OHB
d) cho OA= 10 cm , AB = 12 cm . Tính OH
e) Gọi M là trung điểm của OB, AM cắt OH tại G. Tính OG
a: ΔOAB cân tại O có OH là đường cao
nên OH là trung trực của AB
b: Xét ΔOAB có OA=OB và góc AOB=60 độ
nên ΔOAB đều
c: Xét ΔOHA vuông tại H và ΔOHB vuông tại H có
OA=OB
OH chung
=>ΔOHA=ΔOHB
d: AB=12cm nên HA=6cm
=>OH=căn 10^2-6^2=8cm
e: Xét ΔOAB có
AM,OH là trung tuyến
AM cắt OH tại G
=>G là trọng tâm
=>OG=2/3OH=16/3(cm)
Đúng 0
Bình luận (0)
Cho hình thang ABCD (AB // CD ), có O là giao điểm 2 đường chéo AC và BD.
Đường thẳng song song với AB cắt AD, BD, AC, BC lần lượt tại E, F, G, H.
a) Chứng minh OA . OF = OB . OG
b) Chứng minh EF = GH