Sử dụng hằng đẳng thức hiệu 2 bình phương
Help mik T.T Khó quá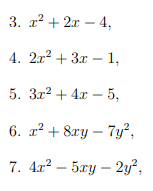

Những câu hỏi liên quan
phân tích đa thức thành nhân tử sử dụng hằng đẳng thức x^4-x^2+2x-1
giúp mik nhé
\(x^4-x^2+2x-1\)
\(=x^4-\left(x^2-2x+1\right)\)
\(=x^4-\left(x-1\right)^2\)
\(=\left(x^2-x+1\right)\left(x^2+x-1\right)\)
hk
tốt
Đúng 0
Bình luận (0)
Giúp e với các anh chị lớp 8 :< Hằng đẳng thức khó quá ạ.
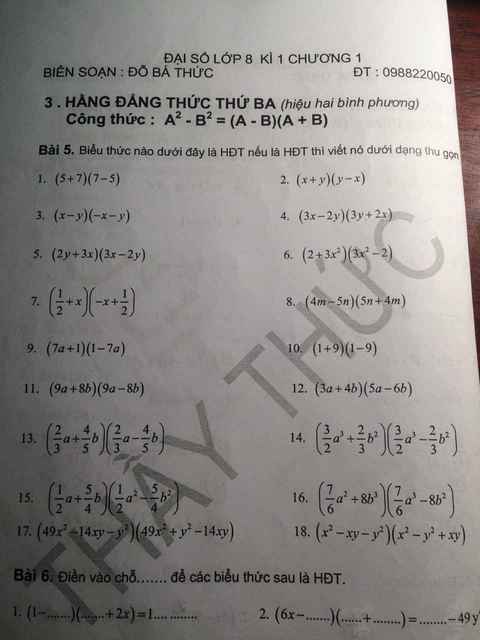
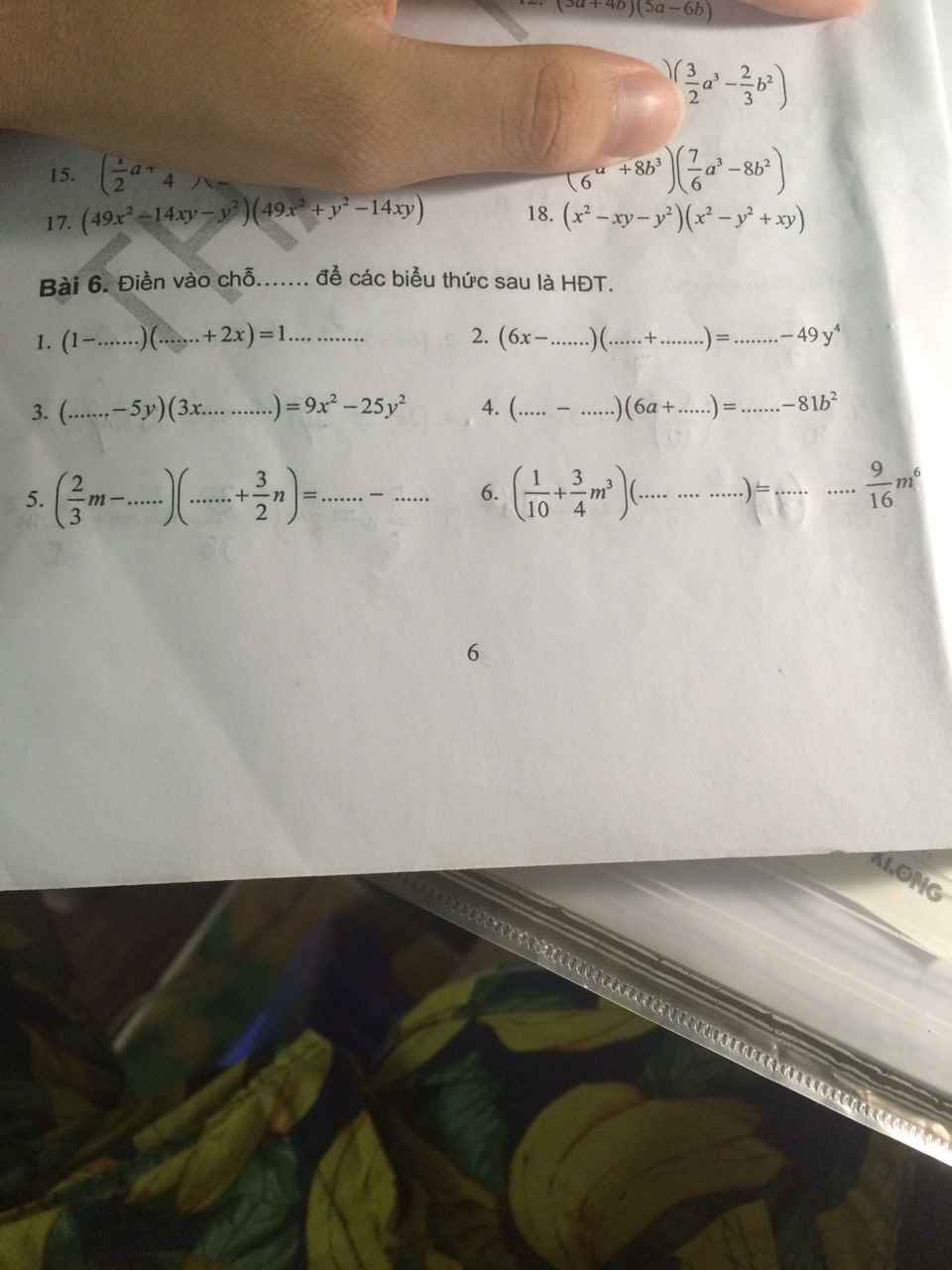
Bài 5:
1) \(\left(5+7\right)\left(7-5\right)=7^2-5^2\)
2) \(\left(x+y\right)\left(y-x\right)=y^2-x^2\)
3) \(\left(x-y\right)\left(-x-y\right)=-\left(x+y\right)\left(x-y\right)=-\left(x^2-y^2\right)=y^2-x^2\)
6) \(\left(2+3x^2\right)\left(3x^2-2\right)=9x^4-4\)
7) \(\left(\dfrac{1}{2}+x\right)\left(-x+\dfrac{1}{2}\right)=\left(\dfrac{1}{2}+x\right)\left(\dfrac{1}{2}-x\right)=\dfrac{1}{4}-x^2\)
8) \(\left(4m-5n\right)\left(5n+4m\right)=\left(4m-5n\right)\left(4m+5n\right)=16m^2-25n^2\)
9) \(\left(7a+1\right)\left(1-7a\right)=\left(1+7a\right)\left(1-7a\right)=1-49a^2\)
10) \(\left(1+9\right)\left(1-9\right)=1-9^2\)
Đúng 1
Bình luận (0)
Bài 5:
11) \(\left(9a+8b\right)\left(9a-8b\right)=81a^2-64b^2\)
13) \(\left(\dfrac{2}{3}a+\dfrac{4}{5}b\right)\cdot\left(\dfrac{2}{3}a-\dfrac{4}{5}b\right)=\dfrac{4}{9}a^2-\dfrac{16}{25}b^2\)
14) \(\left(\dfrac{3}{2}a^3+\dfrac{2}{3}b^2\right)\left(\dfrac{3}{2}a^3-\dfrac{2}{3}b^2\right)=\dfrac{9}{4}a^6-\dfrac{4}{9}b^4\)
17) \(\left(49x^2-14xy-y^2\right)\left(49x^2-14xy+y^2\right)=\left(49x^2-14xy\right)^2-y^4\)
Đúng 1
Bình luận (1)
Xem thêm câu trả lời
bài 5 sử dụng hằng đẳng thức bình phương một tổng ( hiệu) để khai phương
a)\(\sqrt{7+4\sqrt{3}}\)
b)\(\sqrt{8-2\sqrt{12}}\)
c)\(\sqrt{21+6\sqrt{6}}\)
d)\(\sqrt{15-6\sqrt{6}}\)
e)\(\sqrt{29-12\sqrt{5}}\)
g)\(\sqrt{41+12\sqrt{5}}\)
\(\sqrt{7+4\sqrt{3}}=\sqrt{\left(2+\sqrt{3}\right)^2}=2+\sqrt{3}\)
\(\sqrt{8-2\sqrt{12}}=\sqrt{\left(\sqrt{6}-\sqrt{2}\right)^2}=\left|\sqrt{6}-\sqrt{2}\right|=\sqrt{6}-\sqrt{2}\)
\(\sqrt{21+6\sqrt{6}}=\sqrt{\left(3\sqrt{2}-\sqrt{3}\right)^2}=\left|3\sqrt{2}-\sqrt{3}\right|=3\sqrt{2}-\sqrt{3}\)
\(\sqrt{15-6\sqrt{6}}=\sqrt{\left(3-\sqrt{6}\right)^2}=\left|3-\sqrt{6}\right|=3-\sqrt{6}\)
\(\sqrt{29-12\sqrt{5}}=\sqrt{\left(2\sqrt{5}-3\right)^2}=\left|2\sqrt{5}-3\right|=2\sqrt{5}-3\)
\(\sqrt{41+12\sqrt{5}}=\sqrt{\left(6+\sqrt{5}\right)^2}=6+\sqrt{5}\)
Đúng 0
Bình luận (0)
giúp tôi câu này với đang bí quá viết các biểu thức dưới dấu căn sâu về dạng (À+B) bình rồi áp dụng hằng đẳng thức căn A bình +trị tuyệt đối củaA \(\sqrt{7+4\sqrt{3}}\)
Gọi 1/4 số a là 0,25 . Ta có :
a . 3 - a . 0,25 = 147,07
a . (3 - 0,25) = 147,07 ( 1 số nhân 1 hiệu )
a . 2,75 = 147,07
a = 147,07 : 2,75
a = 53,48
Đúng 0
Bình luận (0)
A=\(\sqrt{7+4\sqrt{3}}\) =\(\sqrt{2^2+2.2\sqrt{3}+\left(\sqrt{3}\right)^2}=\sqrt{\left(2+\sqrt{3}\right)^2}=2+\sqrt{3}\)
Đúng 0
Bình luận (0)
các ơi cho mình hỏi trong các hằng đẳng thức có hiệu của hai bình phương nhưng tại sao lại không có tổng của hai bình phương? tổng của hai bình phương là hằng đẳng thức như thế nào?
x^2 + y^2 = (x + y +\(\sqrt{2xy}\))(x + y - \(\sqrt{2xy}\))
Đúng 1
Bình luận (0)
Sử dụng hằng đẳng thức khai triển và thu gọn biểu thức sau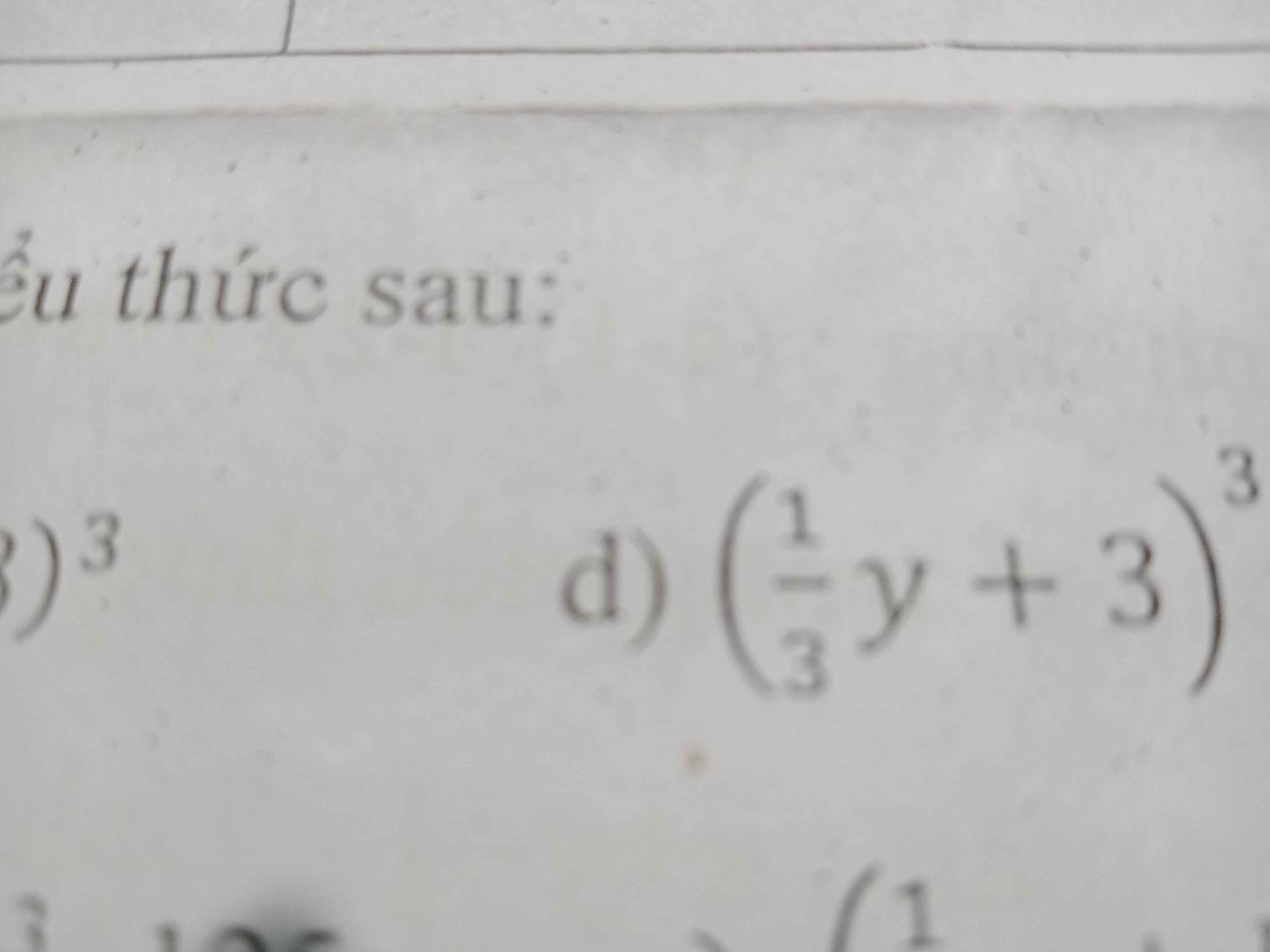
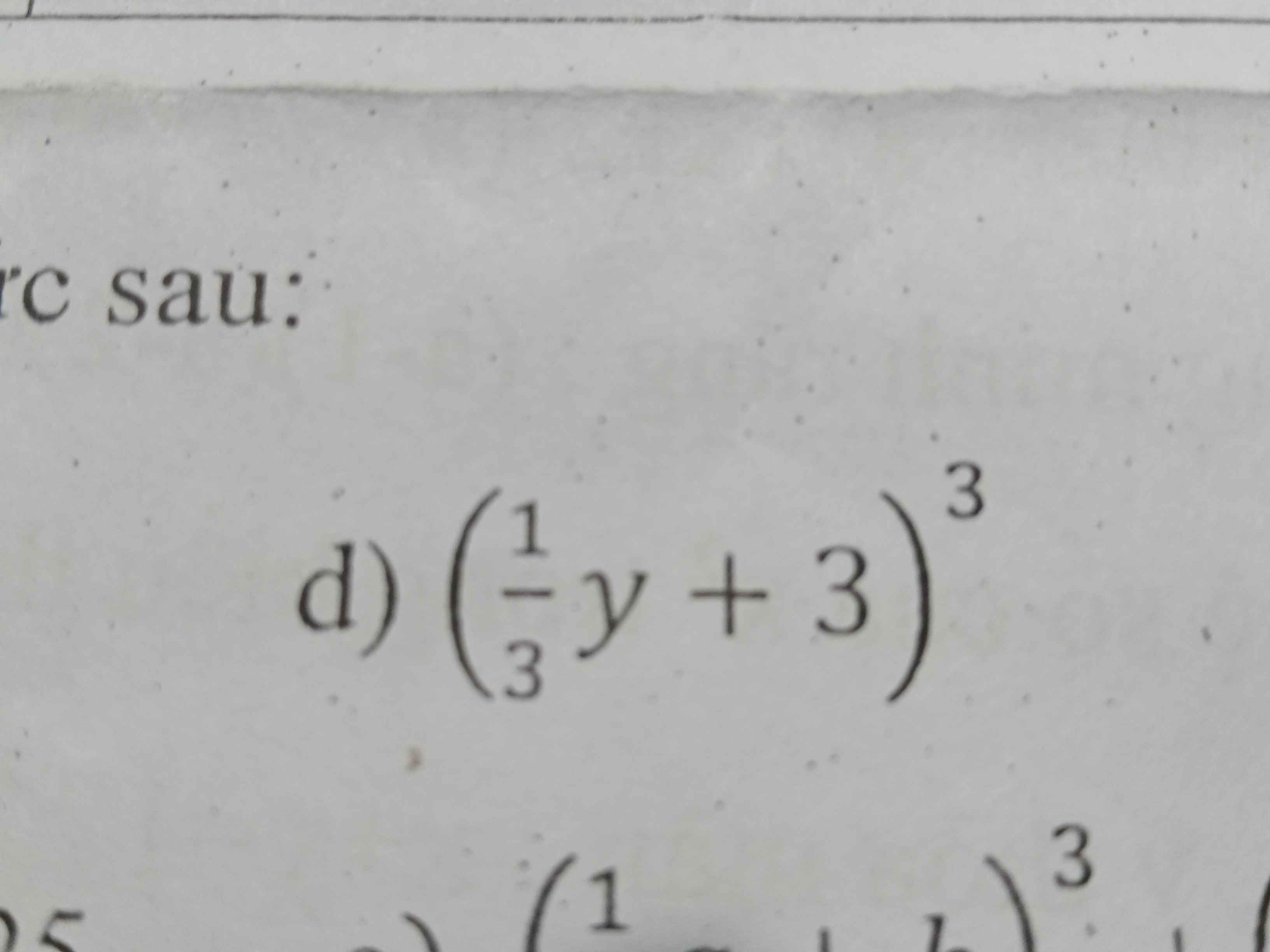
(1𝑦/3+3)^3
(𝑦/3+3)^3
(𝑦/3+3⋅3/3)^3
(𝑦+3⋅3/3)^3
(𝑦+9/3)^3
Đúng 0
Bình luận (0)
\(\left(\dfrac{1}{3}y+3\right)^3=\dfrac{1}{27}y^3+y^2+9y+27\)
Đúng 0
Bình luận (0)
Sử dụng hằng đẳng thức khai triển và thu gọn biểu thức sau (1phần 3y+3)^3
\(\left(\dfrac{1}{3y+3}\right)^3=\dfrac{1}{\left(3y+3\right)^3}=\dfrac{1}{27y^3+81y^2+81y+27}\)
Đúng 0
Bình luận (0)
\(\left(\dfrac{1}{3y+3}\right)^3=\dfrac{1^3}{\left(3y+3\right)^3}=\dfrac{1}{27\left(y^3+3y^2+3y+1\right)}\)
Đúng 0
Bình luận (0)
\(\left(\dfrac{1}{3}y+3\right)^3=\dfrac{1}{27}y^3+y^2+9y+27\)
Đúng 0
Bình luận (0)
Sử dụng hằng đẳng thức bình phương của một tổng, bình phương của một hiểu để khai phương
a) \(\sqrt{17-3\sqrt{32}}\) +\(\sqrt{17+3\sqrt{32}}\)
Có \(\left(\sqrt{17-3\sqrt{32}}+\sqrt{17+3\sqrt{32}}\right)^2\)
\(=\left(\sqrt{17-3\sqrt{32}}\right)^2+2\left(\sqrt{17-3\sqrt{32}}\right)\left(\sqrt{17+3\sqrt{32}}\right)\)\(+\left(\sqrt{17=3\sqrt{32}}\right)^2\)
\(=17-3\sqrt{32}+2\sqrt{\left(17-3\sqrt{32}\right)\left(17+3\sqrt{32}\right)}\)\(+17+3\sqrt{32}\)
\(=34+2\sqrt{17^2-9.32}\)
\(=34+2\sqrt{289-288}\)
\(=34+2\sqrt{1}=34+2=36\)
\(\Rightarrow\sqrt{17-3\sqrt{32}}+\sqrt{17+3\sqrt{32}}\)
\(=\sqrt{36}=6\)
(Vì có \(\hept{\begin{cases}\sqrt{17-3\sqrt{32}}\ge0\\\sqrt{17+3\sqrt{32}}\ge0\end{cases}}\)nên \(\sqrt{17-3\sqrt{32}}+\sqrt{17+3\sqrt{32}}\ge0\))
Đúng 0
Bình luận (0)
Ở cuối dòng 2 mình nhầm dấu + thành dấu = nghe mọi người
Đúng 0
Bình luận (0)
Dấu căn nó không trùm hết cũng mong mọi người thông cảm lun!
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Giải các phương trình bằng cách sử dụng các hằng đẳng thức.
Giúp với ạ!
\(\left(4A\right)\\ a,\\ \Leftrightarrow\left[\left(x-2\right)\left(2x+3\right)\right]\left[\left(x-2\right)\left(2x+3\right)\right]=0\\ \Leftrightarrow\left(-x-5\right)\left(3x+1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}-x-5=0\\3x+1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-5\\x=\dfrac{-1}{3}\end{matrix}\right.\\ b,\\ \Leftrightarrow\left[3\left(2x+1\right)\right]^2-\left[2\left(x+1\right)\right]^2=0\\ \Leftrightarrow\left[3\left(2x+1\right)-2\left(x+1\right)\right]\left[3\left(2x+1\right)+2\left(x+1\right)\right]=0\\ \Leftrightarrow\left(4x+1\right)\left(8x+5\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}4x+1=0\\8x+5=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{-1}{4}\\x=\dfrac{-5}{8}\end{matrix}\right.\\ c,\\ \Leftrightarrow\left[\left(x+1\right)+1\right]^2=0\\ \Leftrightarrow\left(x+1\right)+1=0\\ \Leftrightarrow x+2=0\Rightarrow x=-2\\ d,\\ \Leftrightarrow\left(x-1\right)\left(x-3\right)\left(x+3\right)+\left(x+3\right)=0\\ \Leftrightarrow\left(x+3\right)\left[\left(x-1\right)\left(x+3\right)+1\right]=0\\ \Leftrightarrow\left(x+3\right)\left(x^2-4x+4\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x+3=0\\\left(x+2\right)^2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-3\\x=-2\end{matrix}\right.\)
\(\left(4B\right)\\ a,\\ \Leftrightarrow49-14x+x^2-4\left(x+25\right)^2=0\\ \Leftrightarrow49-14x+x^2-4x^2-40x-100=0\\ \Leftrightarrow3x^2-54x-51=0\\ \Leftrightarrow-3\left(x^2+18x+17\right)=0\\ \Leftrightarrow\left(x+1\right)\left(x+17\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x+1=0\\x+17=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-1\\x=-17\end{matrix}\right.\\ b,\\ \Leftrightarrow4x^2\left(x^2-2x+1\right)-\left(4x^2+4x+1\right)=0\\ \Leftrightarrow x^2-6x=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x-6=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=6\end{matrix}\right.\)
\(c,\\ \Leftrightarrow\left(x+1\right)\left(x^2-x+1\right)=\left(x+1\right)\left(2-x\right)=0\\ \Leftrightarrow\left(x+1\right)\left[\left(x^2-x+1\right)-\left(2-x\right)\right]=0\\ \Leftrightarrow\left(x+1\right)\left(x^1-1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x+1=0\\x-1=0\\x+1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-1\\x=1\\x=-1\end{matrix}\right.\\ d,\\ \Leftrightarrow\left(x-5\right)\left(x+1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x-5=0\\x+1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=5\\x=-1\end{matrix}\right.\)
Đúng 2
Bình luận (2)



























