4a2-12a+1 > hoặc bằng -8
CM bđt trên với mọi a
Những câu hỏi liên quan
Rút gọn biểu thức
4
a
2
+
12
a
+
9
+
4
a
2
-
12
a
+
9
với
-
3
2
≤
a
≤
3
2
ta được A. -4a B. 4a C. -6 D. 6
Đọc tiếp
Rút gọn biểu thức 4 a 2 + 12 a + 9 + 4 a 2 - 12 a + 9 với - 3 2 ≤ a ≤ 3 2 ta được
A. -4a
B. 4a
C. -6
D. 6
Giá trị nhỏ nhất của biểu thức B
4
a
2
-
4
a
+
1
+
4
a
2
-
12
a
+
9...
Đọc tiếp
Giá trị nhỏ nhất của biểu thức B = 4 a 2 - 4 a + 1 + 4 a 2 - 12 a + 9
A. 2
B. 1
C. 4
D. 10
Đáp án đúng : A
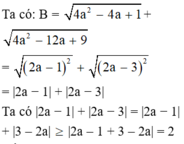
Dấu “=” xảy ra ⇔ 2 a − 1 3 − 2 a ≥ 0 ⇔ 1 2 ≤ a ≤ 3 2
Vậy GTNN của B là 2 khi 1 2 ≤ a ≤ 3 2
Đúng 0
Bình luận (0)
CM các bđt sau
a) x(x+1)(x+2)(x+3)+1 lớn hơn hoặc bằng 0 với mọi số thực x
b) \(\left(a^2+b^2+c^2\right)\left(x^2+y^2+z^2\right)\)lớn hơn hoặc bằng \(\left(ax+by+cz\right)^2\) với mọi số thức a,b,c,x,y,z
giúp mình với
a: =(x^2+3x)(x^2+3x+2)+1
=(x^2+3x)^2+2(x^2+3x)+1
=(x^2+3x+1)^2>=0 với mọi x
b: (a^2+b^2+c^2)(x^2+y^2+z^2)-(ax+by+cz)^2
=a^2x^2+a^2y^2+a^2z^2+b^2x^2+b^2y^2+b^2z^2+c^2x^2+c^2y^2+c^2z^2-a^2x^2-b^2y^2-c^2z^2-2axby-2axcz-2bycz
=(a^2y^2-2axby+b^2x^2)+(a^2z^2-2azcx+c^2x^2)+(b^2z^2-2bzcy+c^2y^2)
=(ay-bx)^2+(az-cx)^2+(bz-cy)^2>=0(luôn đúng)
Đúng 0
Bình luận (0)
Chứng minh BĐT :
Với mọi số thực a,b,c bất kỳ :a^2+b^2+c^2 lớn hơn hoặc bằng ab+bc+ca
\(a^2+b^2+c^2\ge ab+bc+ca\)
\(\Leftrightarrow2a^2+2b^2+2c^2\ge2ab+2bc+2ca\)
\(\Leftrightarrow2a^2+2b^2+2c^2-2ab-2bc-2ca\ge0\)
\(\Leftrightarrow\left(a-b\right)^2+\left(b-c\right)^2+\left(c-a\right)^2\ge0\) (luôn đúng)
-Dấu "=" xảy ra khi \(a=b=c\)
Đúng 1
Bình luận (0)
Phân tích thành nhân tử
a3 -4a2 -12a+27
a3 - 4a2 -12a +27
= a3 + 3a2 - 7a2 -21a +9a +27
= a2(a+3) -7a(a+3) +9(a+3)
= (a+3) (a2 - 7a + 9)
Đây là bài làm của mình. Nếu bạn thấy đúng thì tick hộ mik nhé.
CHÚC BẠN HỌC TỐT NHA ! <3
Đúng 2
Bình luận (1)
P = 4a2 + 4ab + 4b2 - 12a -12b + 12 . Giá trị nhỏ nhất của P = bao nhiêu?
Lời giải:
$P=(4a^2+4ab+b^2)-12a-12b+3b^2+12$
$=(2a+b)^2-6(2a+b)+3b^2-6b+12$
$=(2a+b)^2-6(2a+b)+9+3(b^2-2b+1)$
$=(2a+b-3)^2+3(b-1)^2\geq 0+3.0=0$
Vậy $P_{\min}=0$
Giá trị này đạt tại $2a+b-3=b-1=0$
$\Rightarrow b=1; a=1$
Đúng 0
Bình luận (0)
Lời giải:
$P=(4a^2+4ab+b^2)-12a-12b+3b^2+12$
$=(2a+b)^2-6(2a+b)+3b^2-6b+12$
$=(2a+b)^2-6(2a+b)+9+3(b^2-2b+1)$
$=(2a+b-3)^2+3(b-1)^2\geq 0+3.0=0$
Vậy $P_{\min}=0$
Giá trị này đạt tại $2a+b-3=b-1=0$
$\Rightarrow b=1; a=1$
Đúng 0
Bình luận (0)
1)Tìm 3 số x,y,z sao cho :x^2+5y^2-4xy+10x-22|x+y+z| +26=0
2)CM các BĐT sau
a)(a^2+b^2)(a^1+1) > hoặc = 4a^2b với mọi a,b
b) 1/a + 1/b > hoặc = 4/a+b với mọi a,b>0
c) 1/a+3b + 1/b+3c + 1/c+3a > hoặc = 1/a+2b+c + 1/b+2c+a + 1/c+2a+b
ai làm nhanh mik sẽ tick cho :))
Bài 1 bạn tham khảo tại đây nhé:
Tim x,y,z thoa man : x^2 +5y^2 -4xy +10x-22y +Ix+y+zI +26 = 0 ...
Chúc bạn học tốt!
Cho a, b, c là các số dương thỏa mãn a+b+c=6
CM: a, 1/a + 1/b + 1/c lớn hơn hoặc bằng 3/2
b, a^2/c + b^2/a + c^2/b lớn hơn hoặc bằng 6
(dùng bđt cô-si)
Lời giải:
a. Áp dụng BĐT Cô-si:
$\frac{1}{a}+\frac{a}{4}\geq 1$
$\frac{1}{b}+\frac{b}{4}\geq 1$
$\frac{1}{c}+\frac{c}{4}\geq 1$
Cộng theo vế:
$\frac{1}{a}+\frac{1}{b}+\frac{1}{c}+\frac{a+b+c}{4}\geq 3$
$\Leftrightarrow \frac{1}{a}+\frac{1}{b}+\frac{1}{c}+\frac{6}{4}\geq 3$
$\Leftrightarrow \frac{1}{a}+\frac{1}{b}+\frac{1}{c}\geq \frac{3}{2}$ (đpcm)
Dấu "=" xảy ra khi $a=b=c=2$
b.
Áp dụng BĐT Cô-si:
$\frac{a^2}{c}+c\geq 2a$
$\frac{b^2}{a}+a\geq 2b$
$\frac{c^2}{b}+b\geq 2c$
$\Rightarrow \frac{a^2}{c}+\frac{b^2}{a}+\frac{c^2}{b}+(c+a+b)\geq 2(a+b+c)$
$\Rightarrow \frac{a^2}{c}+\frac{b^2}{a}+\frac{c^2}{b}\geq a+b+c=6$ (đpcm)
Dấu "=" xảy ra khi $a=b=c=2$
Đúng 3
Bình luận (0)
Cho a,b>0. CM: (1+a)[1+b)^2)] lớn hơn hoặc bằng (1+căn ab)^3
(Dùng BĐT)