Cho hình thang cân ABCD có đáy nhỏ AB và đáy lớn CD.Gọi I,J lần lượt là trung điểm AB,CD.Chứng minh:IJ là đường trung trực của đoạn thẳng AB

Những câu hỏi liên quan
Cho hình thang cân ABCD có đáy nhỏ AB và đáy lớn CD .Gọi I ,J lần lượt là trung điểm:CM. a)∆AJB cân. b)Ị là trung trực đoạn thẳng Ab
cho hình thang cân ABCD, đáy nhỏ AB, đáy lớn CD. Gọi I,J lần lượt là trung điểm AB ,CD. Chứng minh tam giác CID cân và IJ là đường trung trực của CD
Cho hình thang ABCD, 2 đáy AB, CD. Gọi M, N lần lượt là trung điểm của AB và CD. Chứng minh :
a) Tam giác ANB cân.
b) MN là đường trung trực của đoạn thẳng AB
Làm theo ABCD là ht cân
a) Xét ΔADN và ΔBCN có:
AD=BC(gt)
^D=^C(gt)
DN=CN(gt)
=> ΔADN =ΔBCN(c.g.c)
=> NA=NB
=>ΔABN cân tại N
b) ΔABN cân tại N(cmt)
Có: NM là đường trung gtuyeens uungs vs cạnh AB
=>NM cx là đg trung trực của AB
Đúng 0
Bình luận (0)
Cho hình thang cân ABCD, hai đáy AB,CD. Gọi M, N lần lượt là trung điểm của AB và CD. Chứng minh :
a) Tam giác ANB cân.
b) MN là trung trực của đoạn thẳng AB.
a)Xét ΔADN và ΔBCN có: AD=BC; góc D= góc C (ABCD là hình thang cân); DN=CN( N là trung điểm của CD). Vậy ΔADN= ΔBCN (c.g.c)→AN=BN→Tam giác ANB cân
b) Vì ΔANB cân, có NM là đường trung tuyến nên đồng thời cũng là đường trung trực của đoạn thẳng AB
Đúng 0
Bình luận (0)
Cho hình thang ABCD có đáy lớn AB=3a, đáy nhỏ CD=a và góc ADC=120o. Gọi M, N lần lượt là trung điểm của AB, CD. CM: AMND là hình thang cân
Cho hình chóp S.ABCD có SA
⊥
(ABCD) đáy ABCD là hình thang vuông có chiều cao ABa Gọi I và J lần lượt là trung điểm AB,CD . Tính khoảng cách giữa đường thẳng IJ và (SAD).
Đọc tiếp
Cho hình chóp S.ABCD có SA ⊥ (ABCD) đáy ABCD là hình thang vuông có chiều cao AB=a Gọi I và J lần lượt là trung điểm AB,CD . Tính khoảng cách giữa đường thẳng IJ và (SAD).
![]()
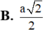
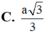
![]()
Cho hình chóp S.ABCD có
S
A
⊥
A
B
C
D
đáy ABCD là hình thang vuông có chiều cao
A
B
a
.
Gọi I và J lần lượt là trung điểm AB,CD . Tính khoảng cách giữa đường thẳng IJ và (SAD). A. a/3 B.
a
2
2
C.
a...
Đọc tiếp
Cho hình chóp S.ABCD có S A ⊥ A B C D đáy ABCD là hình thang vuông có chiều cao A B = a . Gọi I và J lần lượt là trung điểm AB,CD . Tính khoảng cách giữa đường thẳng IJ và (SAD).
A. a/3
B. a 2 2
C. a 3 3
D. a/2
Đáp án D
Gọi I và J lần lượt là trung điểm AB,CD. Tính khoảng cách giữa đường thẳng IJ và (SAD).
S A ⊥ A D , A B ⊥ S A D ,IJ// S A D ⇒ d IJ; S A D = d I; S A D = I A = a 2
Đúng 0
Bình luận (0)
Cho tứ giác ABCD là hình thang có đáy lớn AB=9cm,đáy bé CD =AD=3cm và góc ADC=120 độ.Gọi M,N lần lượt là trung điểm của ABvà CD.Gọi Ilà trung điểm của MN,CI kéo dài cắt AB tại E
Chứng minh
a)Tứ giác AMND là hình thang cân
b)Tứ giác EMCN là hình chữ nhật
Cho hình thang cân abcd đáy AB nhỏ hơn CD.Gọi M,N lần lượt là trung điểm của AD và BC,MN giao BD tại I.Biết AD=10;MI=6;NI=12(cm).Tính diện tích ABCD. Giúp em với ạ
Do M, N là trung điểm của AD và BC nên Mn là đường trung bình của hình thang ABCD
⇒ MN // AB
Do vậy: MI // AB và NI // CD
Lại có: AB = 2MI = 12 ( cm ) ; CD = 2NI = 24 ( cm )
Kẻ AH ⊥ CD tại H và BK ⊥ CD tại K. Khi đó ABCD là hình thang cân nên:
AH = BK và DH = CK = \(\dfrac{DC-AB}{2}=\dfrac{24-12}{6}=6\left(cm\right)\)
Theo định lí Py - ta - go trong △ AHD ta có:
AH2 = AD2 - DH2 ⇒ AH = \(\sqrt{10^2-6^2}=8\left(cm\right)\)
Diện tích hình thang ABCD :
\(S_{ABCD}=\dfrac{\left(AB+CD\right).AH}{2}=\dfrac{\left(12+24\right).8}{2}=144\left(cm^2\right)\)
Đúng 2
Bình luận (0)















