Cho biết a và b là giao điểm của đường thẳng (d): \(y=\dfrac{1}{2}x+1\) và parabol P: \(y=\dfrac{1}{2}x^2\). Xác định điểm M trên trục hoành sao cho chu vi tam giác MAB đạt GTNN.

Những câu hỏi liên quan
Cho parabol(P):y= x^2 và đường thẳng(d):y=x+2
a)Vẽ đồ thị 2 hàm số trên,trên cùng 1 hệ trục toạ độ
b) Xác định toạ độ giao điểm A,B của 2 đồ thị trên
c) Cho điểm M thuộc Parabol(P) có hoành độ là m nhỏ thoả mãn
-1 ≤m ≤2. Chứng minh Diện tích MAB ≤ 27/8
b) Phương trình hoành độ giao điểm của (P) và (d) là:
\(x^2=x+2\)
\(\Leftrightarrow x^2-x-2=0\)
\(\Leftrightarrow x^2-2x+x-2=0\)
\(\Leftrightarrow x\left(x-2\right)+\left(x-2\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left(x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-2=0\\x+1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-1\end{matrix}\right.\)
Thay x=2 vào (P), ta được:
\(y=2^2=4\)
Thay x=-1 vào (P), ta được:
\(y=\left(-1\right)^2=1\)
Vậy: A(2;4) và B(-1;1)
Đúng 0
Bình luận (0)
Cho parabol (P): y = x2 và đường thẳng (d): y = -1/2 x + 3.
a) Tìm tọa độ các giao điểm A và B của (d) và (P).
b) Tìm tọa độ điểm C thuộc trục hoành để chu vi tam giác ABC đạt già trị lớn nhất.
Bài 1. Trong mặt phẳng tọa độ Oxy, cho parabol (P): y - x2a) Vẽ parabol (P)b) Xác định tọa độ các giao điểm A, B của đường thẳng (d): y - x – 2 và (P).c) Tìm tọa độ điểm M trên (P) sao cho tam giác MAB cân tại MBài 2 Cho parabol (P): y x2 và đường thẳng (d): y x + mCMR: (d) luôn cắt (P) tại 2 điểm phân biệta) Giả sử (P) và (d) cắt nhau tại 2 điểm phân biệt có hoành độ x1; x2. Hãy tìm giá trị nhỏ nhất của biểu thức P khi m thay đổiBài 3. Cho parabol (P): y x2 và đường...
Đọc tiếp
Bài 1. Trong mặt phẳng tọa độ Oxy, cho parabol (P): y = - x2
a) Vẽ parabol (P)
b) Xác định tọa độ các giao điểm A, B của đường thẳng (d): y = - x – 2 và (P).
c) Tìm tọa độ điểm M trên (P) sao cho tam giác MAB cân tại M
Bài 2 Cho parabol (P): y = x2 và đường thẳng (d): y = x + m
CMR: (d) luôn cắt (P) tại 2 điểm phân biệt
a) Giả sử (P) và (d) cắt nhau tại 2 điểm phân biệt có hoành độ x1; x2. Hãy tìm giá trị nhỏ nhất của biểu thức P = ![]() khi m thay đổi
khi m thay đổi
Bài 3. Cho parabol (P): y = x2 và đường thẳng (d): y = x + m
Tìm m để đường thẳng (d) cắt (P) tại 2 điểm phân biệt nằm bên phải trục tung
Bài 4. Cho parabol (P): y = x2 và đường thẳng (d): y = x + m
Bài 5. Cho parabol (P): y = x2 và đường thẳng (d): y = mx + 1
Tìm m sao cho (d) cắt (P) tại 2 điểm phân biệt có hoành độ x1; x2 sao cho ![]()
Bài 6. Cho parabol (P) : y = ![]() x2 và đường thẳng (d) : y = mx -
x2 và đường thẳng (d) : y = mx - ![]() m2 + m +1.
m2 + m +1.
a) Với m = 1, xác định tọa độ các giao điểm A, B của (d) và (P).
b) Tìm các giá trị của m để (d) cắt (P) tại hai điểm phân biệt có hoành độ x1, x2 sao cho ![]() .
.
Cho đường thẳng \(\left(d\right):y=\frac{-1}{2}x+2\) và Parabol \(\left(P\right):y=\frac{1}{4}x^2\) trên hệ trục tọa độ Oxy
a, Vẽ Parabol (P) và đường thẳng (d) đã cho
b, Gọi A,B là 2 giao điểm của (d) và (P) . Tìm điểm N trên trục hoành sao cho tam giác NAB cân tại N
trên mặt phẳng oxy cho đường thẳng(D) y=x-6 và parabol(P) y=-x^2
a>tìm tọa độ giao điểm giả sử A là giao điểm có hoành độ âm và B là giao điểm có hoành độ dương.
b>1 điểm M nằm trên phần cong của parabol từ O đến A M#O,A xác định vị trí của M sao cho Samb=15
Cho parabol (P): y = 1/4x^2 và đường thẳng (D) qua 2 điểm A và B trên (P) có hoành độ lần lượt là -2 và 4 a) Khảo sát sự biến thiên b) Viết phương trình của (D) c) Tìm điểm M trên cung AB của (P) (tương ứng hoành độ) x € [-2;4] sao cho tam giác MAB có diện tích lớn nhất
Đề bài : cho Parabol (P): y1/2x^2 và đường thẳng (d):yleft(m+1right)x-dfrac{m-1}{2}(x là ẩn , m là tham số ). tìm tọa độ giao điểm của p và d khi m -2 Gỉai : Pt hoành độ giao điểm của P và d là dfrac{1}{2}x^2-left(m+1right)x+dfrac{m-1}{2}0Thay m-2 vào pt ta đc dfrac{1}{2}x^2-left(-2+1right)x+dfrac{-2-1}{2}0Rightarrowdfrac{1}{2}left(x^2+dfrac{1}{2}x-3right)0Rightarrow x^2+2xdfrac{1}{4}+dfrac{1}{16}-dfrac{1}{16}-30Rightarrowleft(x+dfrac{1}{4}right)^2dfrac{49}{16}Rightarrowleft{{}begin{matrix}xdfr...
Đọc tiếp
Đề bài : cho Parabol (P): y=1/2x^2 và đường thẳng (d):\(y=\left(m+1\right)x-\dfrac{m-1}{2}\)(x là ẩn , m là tham số ). tìm tọa độ giao điểm của p và d khi m = -2
Gỉai : Pt hoành độ giao điểm của P và d là \(\dfrac{1}{2}x^2-\left(m+1\right)x+\dfrac{m-1}{2}=0\)
Thay m=-2 vào pt ta đc \(\dfrac{1}{2}x^2-\left(-2+1\right)x+\dfrac{-2-1}{2}=0\)
\(\Rightarrow\dfrac{1}{2}\left(x^2+\dfrac{1}{2}x-3\right)=0\)
\(\Rightarrow x^2+2x\dfrac{1}{4}+\dfrac{1}{16}-\dfrac{1}{16}-3=0\Rightarrow\left(x+\dfrac{1}{4}\right)^2=\dfrac{49}{16}\)
\(\Rightarrow\left\{{}\begin{matrix}x=\dfrac{6}{4}\\x=-2\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}y=\dfrac{9}{8}\\y=2\end{matrix}\right.\)
Vậy ....
cho hỏi em sai chỗ nào vậy mn
\(\dfrac{1}{2}x^2-\left(-2+1\right)x+\dfrac{-2-1}{2}=0\)
\(\Rightarrow\dfrac{1}{2}x^2+x-\dfrac{3}{2}=0\)
Tới đây dùng \(\Delta\) chứ, nếu bn lấy \(\dfrac{1}{2}\) đặt lm nhân tử chung thì ở đây hơi vô lí
Đúng 2
Bình luận (3)
\(\Delta=b^2-4ac=1-4.\dfrac{1}{2}.\left(-\dfrac{3}{2}\right)=4>0\)
\(\Rightarrow\)Pt có 2 nghiệm phân biệt
\(\left\{{}\begin{matrix}x_1=\dfrac{-b+\sqrt{\Delta}}{2a}=\dfrac{-1+2}{1}=1\\x_2=\dfrac{-b-\sqrt{\Delta}}{2a}=\dfrac{-1-2}{1}=-3\end{matrix}\right.\)
Thay \(x_1=1\) vào \(y=\dfrac{1}{2}x^2\Rightarrow y=\dfrac{1}{2}\)
Thay \(x_2=-3\) vào \(y=-x+\dfrac{3}{2}\Rightarrow y=\dfrac{9}{2}\)
Đúng 1
Bình luận (0)
cho parabol (p) : y=\(-\dfrac{x^2}{2}\)và đường thẳng y=\(-\dfrac{1}{2}x-1\) (d) trên cùng mặt tọa độ .a) vẽ parabol (P) và đường thẳng (d) trên cùng hệ trục tọa độ Oxy
b)tìm tọa độ giao điểm của (p) và (d) bằng phép tính
b: Phương trình hoành độ giao điểm là:
\(-\dfrac{1}{2}x^2=-\dfrac{1}{2}x-1\)
\(\Leftrightarrow-\dfrac{1}{2}x^2+\dfrac{1}{2}x+1=0\)
\(\Leftrightarrow x^2-x-2=0\)
\(\Leftrightarrow\left(x-2\right)\left(x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-1\end{matrix}\right.\)
Thay x=2 vào (P), ta được:
\(y=\dfrac{-2^2}{2}=-2\)
Thay x=-1 vào (P), ta được:
\(y=-\dfrac{1^2}{2}=-\dfrac{1}{2}\)
Đúng 2
Bình luận (0)
Cho parabol (P): ydfrac{1}{4}x^2 và đường thẳng (d) đi qua 2 điểm A, B trên (P) có hoành độ lần lượt là -2, 4.a. Vẽ (P).b. Viết phương trình đường thẳng (d).c. Tìm tọa độ giao điểm M trên cung AB của (P) có hoành độ xinleft[-2;4right] sao cho tam giác ABC có diện tích lớn nhất.(Thầy NVL giúp em với ạ em cảm ơn thầy nhiều ạ)
Đọc tiếp
Cho parabol (P): \(y=\dfrac{1}{4}x^2\) và đường thẳng (d) đi qua 2 điểm A, B trên (P) có hoành độ lần lượt là \(-2,\) 4.
a. Vẽ (P).
b. Viết phương trình đường thẳng (d).
c. Tìm tọa độ giao điểm M trên cung AB của (P) có hoành độ \(x\in\left[-2;4\right]\) sao cho tam giác ABC có diện tích lớn nhất.
(Thầy NVL giúp em với ạ em cảm ơn thầy nhiều ạ)
a. Em tự giải
b. Từ giả thiết ta có \(A\left(-2;1\right)\) và \(B\left(4;4\right)\)
Gọi phương trình (d) có dạng \(y=ax+b\), do (d) qua A và B nên:
\(\left\{{}\begin{matrix}-2a+b=1\\4a+b=4\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=\dfrac{1}{2}\\b=2\end{matrix}\right.\) \(\Rightarrow y=\dfrac{1}{2}x+2\)
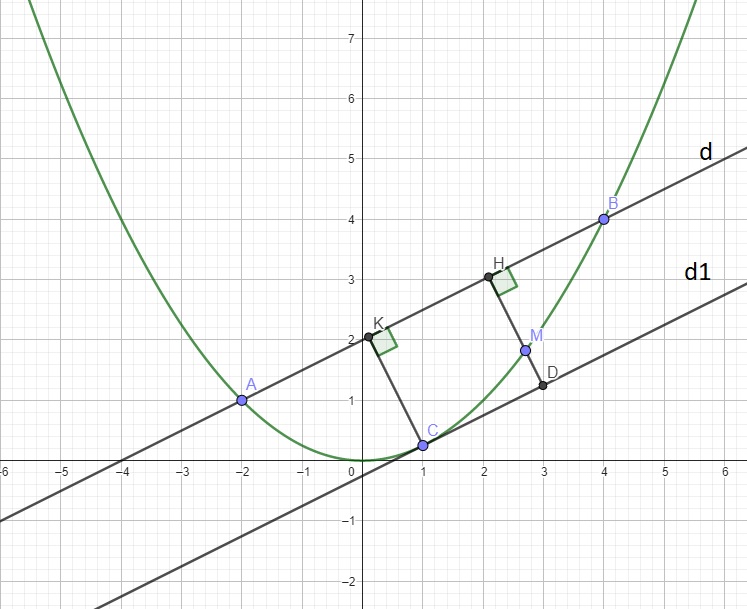
c. Câu này có vài cách giải cho lớp 9, cách nhanh nhất là sử dụng tính chất tiếp tuyến.
Từ M kẻ \(MH\perp AB\Rightarrow S_{ABM}=\dfrac{1}{2}MH.AB\)
Do AB cố định \(\Rightarrow S_{max}\) khi \(MH_{max}\)
Gọi \(d_1\) là đường thẳng song song d và tiếp xúc (P), gọi C là tiếp điểm \(d_1\) và (P)
Do \(d_1\) song song (d) nên pt có dạng: \(y=\dfrac{1}{2}x+b\)
Phương trình hoành độ giao điểm \(d_1\) và (P):
\(\dfrac{1}{4}x^2=\dfrac{1}{2}x+b\Rightarrow x^2-2x-4b=0\) (1)
Do \(d_1\) tiếp xúc (P) \(\Rightarrow\left(1\right)\) có nghiệm kép
\(\Rightarrow\Delta'=1+4b=0\Rightarrow b=-\dfrac{1}{4}\)
Thế vào (1) \(\Rightarrow x_C^2-2x_C+1=0\Rightarrow x_C=1\Rightarrow y_C=\dfrac{1}{4}\) \(\Rightarrow C\left(1;\dfrac{1}{4}\right)\)
Từ C kẻ \(CK\perp d\)
Giả sử HM kéo dài cắt \(d_1\) tại D \(\Rightarrow\) tứ giác CKHD là hình chữ nhật (2 cặp cạnh đối song song và 1 góc vuông)
\(\Rightarrow CK=DH\)
Mà \(DH=MH+MD\ge MH\Rightarrow CK\ge MH\)
\(\Rightarrow MH_{max}=CK\) khi M trùng C
Hay \(M\left(1;\dfrac{1}{4}\right)\)
Đúng 3
Bình luận (5)
Ủa câu c là M hay C em nhỉ?
Đúng 0
Bình luận (5)