Tam giác ABC : AB = 5cm kẻ AH vuông góc với BC . Biết BH = HC = 4cm . Tính AC

Những câu hỏi liên quan
Cho tam giác ABC cân tại A có AB = AC = 5cm, kẻ AH vuông góc với BC (H thuộc BC).
a) Chứng minh: BH = HC và góc BAH = góc CAH
b) Tính độ dài BH biết AH = 4cm.
c) Kẻ HD vuông góc với AB (D thuộc AB), kẻ EH vuông góc với AC (E thuộc AC). Tam giác ADE là tam giác gì ? Vì sao ?
a: ΔABC cân tại A
mà AH là đường cao
nên H là trung điểm của BC và AH là phân giác của góc BAC
=>góc BAH=góc CAH
b: \(BH=\sqrt{5^2-4^2}=3\left(cm\right)\)
c: Xét ΔADH vuông tại D và ΔAEH vuông tại E có
AH chung
góc DAH=góc EAH
Do đó: ΔADH=ΔAEH
=>AD=AE
=>ΔADE cân tại A
Đúng 0
Bình luận (0)
câu 1 Cho tam giác ABC có các góc B, C nhọn. Kẻ AH vuông góc với BC. Biết AB = 20cm, BH = 16cm, HC = 5cm. Tính AH, AC.
câu 2 Cho tam giác ABC có các góc B, C nhọn. Kẻ AH vuông góc với BC, biết AC = 15cm, HB = 5cm, HC = 9cm . Tính độ dài cạnh AB.
Câu 1:
Xét tam giác ABH vuông tại H, ta có:
AB2 = AH2 + HB2 (định lý Py-ta-go)
202 = AH2 + 162
400 = AH2 + 256
AH2 = 400 - 256
AH2 = 144
AH = \(\sqrt{144}\)= 12 (cm)
Xét tam giác AHC vuông tại H, ta có:
AC2 = AH2 + HC2 (định lý Py-ta-go)
AC2 = 122 + 52
AC2 = 144 + 25
AC2 = 169
AC = \(\sqrt{169}\)= 13 (cm)
Vậy AH = 12 cm
AC = 13 cm
Bài 2:
Xét tam giác AHC vuông tại H, ta có:
AC2 = AH2 + HC2 (định lý Py-ta-go)
152 = AH2 + 92
225 = AH2 + 81
AH2 = 225 - 81
AH2 = 144
AH = \(\sqrt{144}\)= 12 (cm)
Xét tam giác AHB vuông tại, ta có:
AB2 = AH2 + HB2 (định lý Py-ta-go)
AB2 = 122 + 52
AB2 = 144 + 25
AB2 = 169
AB = \(\sqrt{169}\)= 13 (cm)
Vậy AB = 13 cm
Đúng 1
Bình luận (0)
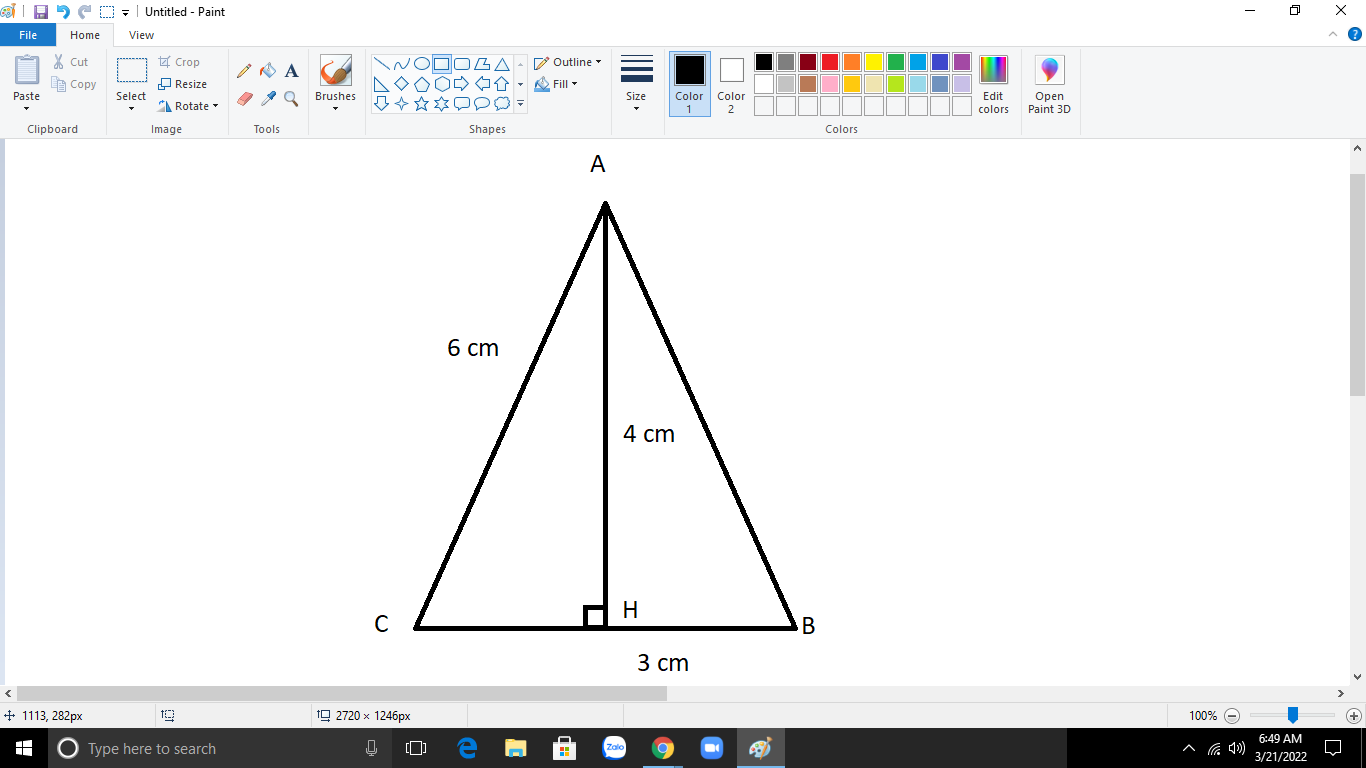
Cho tam giác nhọn ABC kẻ AH vuông góc với BC Biết AH = 4cm BH= 3cm AC=6cm Tính độ dài AB và HC
\(\text{Xét }\Delta AHB\text{ vuông tại H có:}\)
\(AB^2=AH^2+BH^2\text{(định lí Py ta go)}\)
\(\Rightarrow AB^2=4^2+3^2=16+9=25\left(cm\right)\)
\(\Rightarrow AB=\sqrt{25\left(cm\right)}=5\left(cm\right)\)
\(\text{Xét }\Delta AHC\text{ có:}\)
\(AC^2=AH^2+HC^2\)
\(\Rightarrow HC^2=AC^2-AH^2\text{(định lí Py ta go đảo)}\)
\(\Rightarrow HC^2=6^2-4^2=36-16=20\left(cm\right)\)
\(\Rightarrow HC=\sqrt{20}\left(cm\right)\)
Đúng 0
Bình luận (0)
cho tam giác ABC cân ở A có AB=AC=5cm; kẻ AH vuông góc vs BC ( H thuộc BC)
a, CM BH=HC và BAH = CAH
b, tính độ dài BH biết AH = 4cm
c, kẻ HD vuông góc vs AB( D thuộc AB), kẻ EH vuông góc vs AC( E thuộc AC)
d, tam giác ADE là tam giác gì? vì sao?
a, Ta có ∆ABC cân ở A(gt)
AH\(\perp\) BC=>AH là đường cao
(1)=>AH đồng thời là trung tuyến=>HB=HC
(2)=>AH đồng thời là phân giác=>góc BAH=góc CAH
b, Áp dụng định lí pyta go cho ∆ABH ta có
AB2=AH2+BH2 =>52=42+HB2=>HB=√52--42=3
Đúng 0
Bình luận (0)
d, Xét ∆DHB và ∆EHC có
Góc HDB=góc HEC =90°(HD\(\perp\) AB, HE vuông góc ACgt)
Góc B=góc C ( tam giác ABC cân tai A gt)
HB =HC (cmt)
=> ∆DHB=∆EHC(ch-cgv)=>HD=HE=>∆HDE cân tại H
Đúng 0
Bình luận (0)
cho tam giác ABC , kẻ AH vuông góc với BC . biết AB=5cm , BH=8cm . tính độ dài các cạnh AH , HC , AC
Bạn tham khảo nhé!
https://olm.vn/hoi-dap/detail/33236210534.html
MÌNH LẠI PHẢI RA TAY ROOIFVOO LÝ VL
LUÔN
Cho tam giác ABC là tam giác nhọn, kẻ AH vuông góc với BC và AB=5cm AH=4cm BC=9cm. Tính HC và AC
Áp dụng định lí Py-ta-go vào tam giác ABH vuông tại H, ta có:
AH²+BH²=AB²
AH²=AB²−BH²
AH²=52−32
⇒AH²=16
⇒AH=4(cm)
Ta có:
BH+HC=BC
⇒HC=BC−BH
⇒HC=8−3
⇒HC=5(cm)
Áp dụng định lí Py-ta-go vào tam giác AHC vuông tại H, ta có:
AH²+HC²=AC²
42+52=AC²
⇒AC²=41
⇒AC=√41(cm)
Vậy HC = 5 cm, AC = √41 cm
#Tuyên#
Cho tam giác ABC, kẻ AH vuông góc BC, biết AB=5cm, BH=3cm, BC=8cm. Tính độ dài các cạnh AH, HC, AC
Hình bé tự vẽ nhá.
Áp dụng định lý Py-ta-go vào tam giác ABH vuông tại H,có :
AH2 +BH2 =AB2
AH2 = AB2 - BH2
AH2 = 52 - 32
=>. AH2 = 16
AH = 4 (cm)
Theo đề, có : AH vuông góc với BC
=> H thuộc BC
=> BH + HC = BC
HC = 8 - 3
HC = 5 (cm)
Áp dụng định lý Py-ta-go vào tam giác AHC vuông tại H, có :
AH2 + HC2 = AC2
42 + 52 = AC2
=> AC2 = 41
AC = \(\sqrt{41}\)
Đúng 1
Bình luận (0)
Áp dụng đ.lí pytago trong tam giác vuông ABH ta có;
AH2+BH2=AB2
=>AH2=AB2-BH2=52-32
=>AH2=25-9=16
=>AH=+(-)4
mà AH>0 =>AH=4 cm
Lại có;
BH+HC=BC
=>HC=BC-BH=8-3
=>HC=5 cm
Áp dụng đ.lí pytago trong tam giác vuông AHC ta có:
AC2=AH2+HC2
=>AC2=42+52=16+25
=>AC2=41
=>AC=+(-)\(\sqrt{41}\)
Mà AC >0 =>AC=\(\sqrt{41}\)cm
Vậy AH=4 cm; HC=5 cm ; AC= \(\sqrt{41}\)cm
Đúng 0
Bình luận (0)
(AH)
Tam giác ABH vuông tại H
=> BA2=AH2+BH2
<=> AH2=BA2-BH2=52-32=25-9=16
AH=4 cm
(HC)
Ta có BH+HC=BC
=> HC=BC-BH=8-3=5cm
(AC)
Trong tam giác AHC vuông tại H:
=> AC2=AH2+HC2=42+52=41
AC=\(\sqrt{41}cm\)
tik nhá các bn
Đúng 0
Bình luận (0)
cho tam giác ABC, kẻ AH vuông góc BC. biết AB = 5cm; BH = 3cm; BC = 8cm. tính độ dài các cạnh AH, HC, AC?
- Ta có tam giác ABC vuông tại H
Áp dụng định lí Pi-ta-go có:
\(AB^2-BH^2=AH^2=5^2-3^2=16\Rightarrow AH=4\)
Tương tự ta có:...(bn tự làm)
Tam giác AHC vuông tại H
=> cũng như trên
Đúng 0
Bình luận (0)
Tự vẽ nhé
Áp dụng định lí Pi-ta-go vào tam giác ABH vuông tại H , ta có:
AH\(^2\)+ BH\(^2\)= AB\(^2\)
AH\(^2\)= \(AB^2-BH^2\)
\(AH^2=5^2-3^2\)
\(=>AH^2=16\)
\(AH=4cm\)
Theo đề, ta có: AH vuông góc với BC
=> H thuộc BC
=> BH + HC = BC
HC = 8 - 3
HC=5 cm
Áp dụng định lý Pi-ta-go vào tam giác AHC vuông tại H, ta có:
\(AH^2+HC^2=AC^2\)
\(4^2+5^2=AC^2\)
=> \(AC^2=41\)
=> \(AC=\sqrt{41}\)
Đúng 1
Bình luận (0)
+) Áp dụng định lí Pytago vào \(\Delta ABH\)vuông tại H có
\(AB^2=BH^2+AH^2\)
\(AH^2=AB^2-BH^2\)
\(AH^2=5^2-3^2=16\)
\(AH=4\left(cm\right)\)
+) HC = BC - BH
HC = 8 - 3
HC = 5 (cm)
+) Áp dụng định lí Pytago vào \(\Delta ACH\)vuông tại H có
\(AC^2=AH^2+HC^2\)
\(AC^2=3^2+5^2=34\)
\(AC=\sqrt{34}\)
Vậy AH = 4 (cm); HC = 5 (cm); \(AC=\sqrt{34}\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho tam giác ABC nhọn. kẻ AH vuông góc với BC. Tính chu vi tam giác ABC biết AB = 5cm, AH = 4cm, HC = 12cm
Áp dụng định lý Pitago, ta có: \(AC^2=AH^2+HC^2\)
\(\Rightarrow20^2=12^2+HC^2\)
\(\Rightarrow HC^2=20^2-12^2\)
\(\Rightarrow HC^2=400-144=256\)
\(\Rightarrow HC=16\left(cm\right)\)
Áp dụng định lý Pitago, ta có: \(AB^2=BH^2+AH^2\)
\(\Rightarrow AB^2=5^2+12^2\)
\(\Rightarrow AB^2=25+144=169\)
\(\Rightarrow AB=13\left(cm\right)\)
Vậy CV tam giác ABC là
\(20+5+16+13=54\left(cm\right)\)
a/ Cho tam giác ABC vuông cân tại B. Tính AC biết AB là 5cm
b/ Cho ttam giác ABC vuông cân tại B. Tính BC biết AC=4cm. Kẻ BH vuông góc với AC tại H. Chứng minh BH=AH=HC
(nhanh lên nhé một lát nữa mình học thêm)
huhu tí nữa mình học thêm rồi nhanh lên nhé






























