a) Tam giác AGP và PGB có chung đường cao hạ từ đỉnh G và AP = PB nên S_AGP = S_PGB

Tương tự, ta có: S_BGM = S_MGC và S_CGN = S_NGA.

Vì G là trọng tâm DABC Þ AG = 2GM.

Þ S_BGM = 1 2 S_ABG Þ S_BGM = S_AGP = S_PGB.

Chứng minh tương tự, ta suy ra được:

S_AGP = S_PGB = S_BGM = S_MGC = S_CGN = S_NGA

b) Sử dụng kết quả câu a) ta có diện tích mỗi tam giác bằng 1 6  S_ABC, từ đó suy ra ĐPCM.

Em tham khảo tại link này nhé.

Câu hỏi của truong nhat linh - Toán lớp 7 - Học toán với OnlineMath

Kéo dài BG cắt AC tại N; CG cắt AB tại M

Có : S_AGC = \(\frac{1}{2}\)h.GC ; S_BGC = \(\frac{1}{2}\). k. GC  mà S_AGC = S_GBC nên h = k

Mặt khác, S_GAM   = \(\frac{1}{2}\)h.GM ; S_GBM = \(\frac{1}{2}\)k. GM 

=> S_GAM = S_GBM 

Lại có : tam giác GAM; GBM đều chung chiều cao hạ từ G xuống AB => đáy MA = MB => M là trung điểm của AB => CM là trung tuyến 

+) Tương tự, từ S_GAB = S_GBC => N là trung điểm của AC => BN là trung tuyến

BN cắt CM tại G => G là trọng tâm tam giác ABC

a)

Ta có:

     G là trọng tâm của tam giác ABC (giao điểm của ba đường trung tuyến);

     H là trực tâm của tam giác ABC (giao điểm của ba đường cao);

     I là giao điểm của ba đường phân giác của tam giác ABC;

     O là giao điểm của ba đường trung trực của tam giác ABC (Đường trung trực đi qua trung điểm của cạnh và vuông góc với cạnh tại trung điểm đó).

Mà tam giác ABC đều nên trong tam giác ABC đường trung tuyến đồng thời là đường cao và là đường phân giác.

Vậy bốn điểm G, H, I, O trùng nhau hay nếu tam giác ABC đều thì bốn điểm G, H, I, O trùng nhau.

b) 

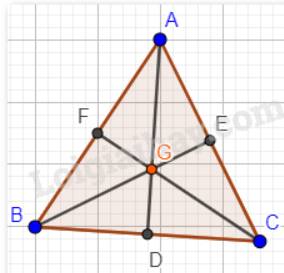
Giả sử trong tam giác ABC có hai điểm trùng nhau là H (trực tâm của tam giác) và I (giao của ba đường phân giác).

Hay AD, BE, CF vừa là đường cao, vừa là đường phân giác của tam giác ABC.

Xét tam giác ADB và tam giác ADC có:

\(\widehat {BAD} = \widehat {CAD}\) ( vì AD là tia phân giác của góc BAC)

AD chung;

\(\widehat {ADB} = \widehat {ADC}(=90^0)\) (vì \(AD \bot BC\));

Vậy \(\Delta ADB = \Delta ADC\)(g.c.g). Suy ra: AB = AC( 2 cạnh tương ứng). (1)

Tương tự ta có: \(\Delta AEB = \Delta CEB\)(c.g.c). Suy ra: AB = BC ( 2 cạnh tương ứng). (2)

Từ (1) và (2) suy ra: AB = BC = AC.

Vậy tam giác ABC đều hay nếu tam giác ABC có hai điểm trong bốn điểm G, H, I, O trùng nhau thì tam giác ABC là tam giác đều.