Biết sinα = 0,75. Vậy cosα =

Những câu hỏi liên quan
Cho
A
B
C
^
60
0
và ∆ABC tam giác nhọna, Tính sinα, tanα, cotα, biết cosα
1
5
b, Tính cosα, tanα, cotα, biết sinα
2
3
c, Cho tanα 2. Tính sinα, cosα, cotαd, Cho cotα 3. Tính sinα, cosα, tanα
Đọc tiếp
Cho A B C ^ = 60 0 và ∆ABC tam giác nhọn
a, Tính sinα, tanα, cotα, biết cosα = 1 5
b, Tính cosα, tanα, cotα, biết sinα = 2 3
c, Cho tanα = 2. Tính sinα, cosα, cotα
d, Cho cotα = 3. Tính sinα, cosα, tanα
a, Tìm được sinα = 24 5 , tanα = 24 , cotα = 1 24
b, cosα = 5 3 , tanα = 2 5 , cotα = 5 2
c, sinα = ± 2 5 , cosα = ± 1 5 , cotα = 1 2
d, sinα = ± 1 10 , cosα = ± 3 10 , tanα = 1 3
Đúng 0
Bình luận (0)
Bài 1: Biết rằng sinα = 0,6. Tính cosα và tgα.
Bài 2: Biết rằng cosα = 0,7. Tính sinα và tgα.
Bài 3: Biết rằng tgα = 0,8. Tính sinα và cosα.
Bài 4: Biết cosx = \(\dfrac{1}{2}\), tính P = 3sin2x + 4cos2x.
Bài 1:
\(\cos\alpha=\sqrt{1-\dfrac{9}{25}}=\dfrac{4}{5}\)
\(\tan\alpha=\dfrac{3}{5}:\dfrac{4}{5}=\dfrac{3}{4}\)
Bài 2:
\(\sin\alpha=\sqrt{1-\dfrac{49}{100}}=\dfrac{\sqrt{51}}{10}\)
\(\tan\alpha=\dfrac{\sqrt{51}}{7}\)
Đúng 1
Bình luận (0)
A = \(\dfrac{\text{sinα + cosα}}{\text{sinα - cosα}}\) Tính α biết tan α = \(\sqrt{3}\)
\(A=\dfrac{\dfrac{sina}{cosa}+\dfrac{cosa}{cosa}}{\dfrac{sina}{cosa}-\dfrac{cosa}{cosa}}=\dfrac{tana+1}{tana-1}=\dfrac{\sqrt{3}+1}{\sqrt{3}-1}=2+\sqrt{3}\)
Đúng 1
Bình luận (0)
sinα = 2, tanα = 2, cotα = 2 biết cosα = \(\dfrac{1}{3}\) α∈ (0;\(\dfrac{\pi}{2}\))
Tính cosα
$\sin \alpha =2$?? $\sin \alpha \in [-1;1]$ với mọi $\alpha$ mà bạn. Bạn xem lại đề.
Đúng 0
Bình luận (1)
Tìm cosα, tanα, cotα. biết sinα = 1 5
Tìm sinα, cotα, tanα biết cosα = 1 5
Gợi ý: Sử dụng công thức: sin 2 α + cos 2 α = 1
Đúng 0
Bình luận (0)
Biết
sin
α
-
cos
α
m
.Tính:
sin
3
α
-
cos
3
α
Đọc tiếp
Biết sin α - cos α = m .Tính: sin 3 α - cos 3 α
![]()
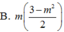
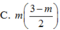
![]()
Tìm góc nhọn α , biết sinα = cosα .
`sin α=cos α`
`<=> sinα : cosα = cosα : cosα`
`<=> tanα=1`
`<=>α=45^o`
Đúng 0
Bình luận (0)
Lời giải:
Xét tam giác $ABC$ vuông tại $A$ có $\widehat{B}=\alpha$
$\cos \alpha = \frac{AB}{BC}$
$\sin \alpha = \frac{AC}{BC}$
$\cos \alpha = \sin \alpha \Leftrightarrow AB=AC\Leftrightarrow ABC$ là tam giác vuông cân
$\Leftrightarrow \widehat{B}=\widehat{C}=45^0$
Vậy $\alpha = 45^0$
Đúng 0
Bình luận (0)
Cho biết
cos α + sin α cos α - sin α = 5
Tính tanα
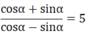
⇔ cosα + sinα = 5(cosα - sinα)
⇔ cosα + sinα = 5cosα - 5sinα
⇔ 6sinα = 4cosα
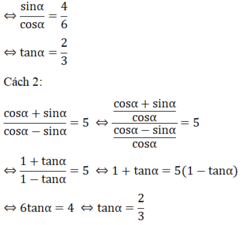
Đúng 0
Bình luận (0)