HELP
tìm các số nguyên x để x4 - x2 + 2x + 2 là số chính phương
Tìm x để mệnh đề chứa biến sau đúng:
a) “ x là số chính phương và 3 < x < 20
b) “ x là số tự nhiên và x2+2x-3=0 "
c) “ x là số nguyên âm thỏa mãn x2≤4
a. \(x=\left\{4;9;16\right\}\)
b. \(x=1\)
c. \(x=\left\{-2;-1\right\}\)
Tìm tất cả các số nguyên dương x để x
2 + 8x là số chính phương.
Bài 1. Tìm tất cả các số nguyên dương x để x2 + 8x là số chính phương.
-Đặt \(x^2+8x=a^2\)
\(\Rightarrow x^2+8x+16=a^2+16\)
\(\Rightarrow\left(x+4\right)^2-a^2=16\)
\(\Rightarrow\left(x+a+4\right)\left(x-a+4\right)=16\)
-Vì \(x,a\) là các số nguyên dương \(\Rightarrow x+a+4>x-a+4\) và \(16=16.1=8.2=4.4\)
\(\Rightarrow x+a+4=16;x-a+4=1\Rightarrow x=\dfrac{9}{2};a=\dfrac{15}{2}\left(loại\right)\)
\(x+a+4=8;x-a+4=2\Rightarrow x=1;a=3\left(nhận\right)\)
\(x+a+4=4;x-a+4=4\Rightarrow x=a=0\left(nhận\right)\)
-Vậy \(x\in\left\{0;1\right\}\)
Tìm số nguyên x sao cho x2+2x+2 là số chính phương
đăt. x^2 + 2x +1 +1 = n^2 ( n dương) suy ra n^2 - (x + 1)^2 = 1 hay (n-x-1)(n+x+1) = 1.1
suy ra n - x -1 = 1 và n + x + 1 =1 suy ra n = 1; x = -1.liên hệ 0972315132
Tìm các số nguyên x để x2 - 2x - 14 là số chính phương?
Để x^2 - 2x - 14 là số chính pương
<=> x^2 - 2x - 14 = y^2
<=> x^2 - 2x + 1 - 15 = y^2
<=> (x - 1)^2 - 15 = y^2
<=> (x - 1)^2 - y^2 = 15
<=> (x - y - 1)(x + y - 1) = 3*5 = 1*15 = -5*(-3) = -15*(-1)
Vì x - y - 1 < x + y - 1
=> TH1: x - y - 1 = 3 ; x + y - 1 = 5
<=> x - y = 4 ; x + y = 6
<=> x = 5
TH2: x - y - 1 = 1 ; x + y - 1 = 15
<=> x - y = 2 ; x + y = 16
<=> x = 9
TH3: x - y - 1 = -5 ; x + y - 1 = -3
<=> x - y = -4 ; x + y = -2
<=> x = -3
TH4: x - y - 1 = -15 ; x + y - 1 = -1
<=> x - y = -14 ; x + y = 0
<=> x = -7
Vậy x = 5; x = 9; x = -3; x = -7
NHỚ LIKE CHO MÌNH NHÉ! MÌNH CẢM ƠN!
bạn có thể giải ra cho tớ hiểu được không ??????....
Cho phương trình 4 - x - a . log 3 x 2 - 2 x + 3 + 2 - x 2 + 2 x . log 1 3 2 x - a + 2 = 0 . Tập tất cả các giá trị của tham số a để phương trình có 4 nghiệm x 1 ; x 2 ; x 3 ; x 4 thỏa mãn là (c;d). Khi đó giá trị biểu thức T = 2 c + 2 d bằng:
A. 5
B. 2
C. 3
D. 4
Cho các số nguyên dương x, y thỏa mãn điều kiện x2 + y2 + 2x(y+1) - 2y là số chính phương. CMR: x = y
cmr : nếu x,y là các số nguyên thỏa mãn hệ thức
2^x2+x=3y^2+y
thì (x-y),(2x+2y+1) và (3x+3y+1) là các số chính phương
Tìm tất cả các giá trị thực của tham số m để phương trình sau có nghiệm x ∈ [ 1 ; 2 ] .
x 4 + 16 x 4 + 4 ( x 2 + 4 x 2 ) - 12 ( x - 2 x ) = m
A. - 13 ≤ m ≤ 11
B. - 15 ≤ m ≤ 9
C. - 15 < m < 9
D. - 16 ≤ m ≤ 9
Đáp án là B.
Đặt t = x - 2 x Đạo hàm t , = 1 + 2 x 2 > 0
Do đó t ( 1 ) ≤ t ≤ t ( 2 ) , ∀ x ∈ [ 1 ; 2 ] , suy ra - 1 ≤ t ≤ 1
Ta có x 2 + 4 x 2 = t 2 + 4 , x 4 + 16 x 4 = ( x 2 + 4 x 2 ) 2 - 8 = ( t 2 + 4 ) 2 - 8 = t 4 + 8 t 2 + 8
Phương trình đã cho trở thành
t 4 + 8 t 2 + 8 - 4 ( t 2 + 4 ) - 12 t = m ⇔ t 4 + 4 t 2 - 12 t = m + 8 ( * )
Phương trình đã cho có nghiệm trong đoạn [1;2] khi và chỉ khi phương trình (*) có nghiệm trong [-1;1] Xét hàm số y=f(t)= t 4 + 4 t 2 - 12 t trên [-1;1]
Đạo hàm y , = 4 t 8 + 8 t - 12 , t ∈ ( - 1 ; 1 ) . y , = 4 ( t - 1 ) ( t 2 + t + 3 ) < 0 , ∀ t ∈ ( - 1 ; 1 )
Bảng biến thiên:
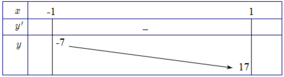
Do đó để phương trình đã cho có nghiệm trên [1;2] thì - 7 ≤ m + 8 ≤ 17 ⇔ - 15 ≤ m ≤ 9
Tìm các số nguyên x để biểu thức \(x^4+2x^3+2x^2+x+3\) là một số chính phương
Giải:
Dùng biến đổi tương đương chứng minh được:
\(\left(x^2+x+2\right)^2=x^4+5x^3+4x+4>x^4+2x^3+2x^2+x+3>\) \(x^4+2x^3+x^2=\left(x^2+x\right)^2\)
\(\Rightarrow x^4+2x^3+2x^2+x+3=\left(x^2+x+1\right)^2\)
\(\Leftrightarrow x^4+2x^3+2x^2+x+3=x^4+2x^3+3x^2+2x+1\)
\(\Leftrightarrow x^2+x-2=0\Leftrightarrow\orbr{\begin{cases}x=1\\x=-2\end{cases}}\)
Vậy \(x=1\) hoặc \(x=-2\) thì phương trình trên là số chính phương
dùng phương pháp hệ số bất định ý bạn gọi đa thức đó là bình phương của đa thức (x^2+ax+b)^2 rồi khai triển là ok