Cho tam giác ABC có trọng tâm G, trực tâm H, tâm đường tròn ngoại tiếp O. gọi D, E, F lần lượt là trung điểm các cạnh BC, CA, AB.
Phép vị tự tâm G tỉ số -1/2 biến tam giác ABC thành
A. Tam giác GBC
B. Tam giác DEF
C. Tam giác AEF
D. Tam giác AFE
Phép vị tự tâm G tỉ số -1/2 biến A thành D; biến B thành E; biến C thành F ⇒ biến tam giác ABC thành tam giác DEF.
Đáp án B
Đúng 0
Bình luận (0)
Cho tam giác ABC có trọng tâm G, trực tâm H, tâm đường tròn ngoại tiếp O. gọi D, E, F lần lượt là trung điểm các cạnh BC, CA, AB. Phép vị tự tâm G tỉ số -1/2 biến:
A. Điểm A thành điểm G
B. Điểm A thành điểm D
C. Điểm D thành điểm A
D. Điểm G thành điểm A
G D → = - 1 / 2 G A → ⇒ phép vị tự tâm G tỉ số -1/2 biến A thành D.
Đáp án B.
Đúng 0
Bình luận (0)
Cho tam giác ABC có trọng tâm G, trực tâm H, tâm đường tròn ngoại tiếp O. gọi D, E, F lần lượt là trung điểm các cạnh BC, CA, AB.Phép vị tự tâm G tỉ số -1/2 biến
A
H
→
thành A.
O
D
→
B.
D
O
→
C.
H
K...
Đọc tiếp
Cho tam giác ABC có trọng tâm G, trực tâm H, tâm đường tròn ngoại tiếp O. gọi D, E, F lần lượt là trung điểm các cạnh BC, CA, AB.
Phép vị tự tâm G tỉ số -1/2 biến A H → thành
A. O D →
B. D O →
C. H K →
D. K H →
Gọi A’ là điểm đối xứng với A qua tâm O.
chứng minh BHCA’ là hình bình hành, suy ra H, A', D thẳng hàng và DO là đường trung bình của tam giác AHA’ ⇒ D O → = - 1 / 2 A H → ⇒ phép vị tự tâm G tỉ số -1/2 biến A H → thành DO → .
Đáp án B
Đúng 0
Bình luận (0)
Cho tam giác ABC. Gọi O, G, H lần lượt là tâm đường tròn ngoại tiếp, trọng tâm. trực tâm của tam giác ABC. Gọi I là tâm đường tròn đi qua trung điểm của ba cạnh AB, BC, CA. Chứng minh:
b) HA + HB + HC = 2HO = 3HG
c) OH =2OI
Cho
∆
A
B
C
có trọng tâm G. Gọi M, N, P lần lượt là trung điểm của các cạnh AB, BC, CA. Phép vị tự nào sau đây biến tam giác ABC thành tam giác NPM? A.
V
A
;
-
1
2
B.
V
G...
Đọc tiếp
Cho ∆ A B C có trọng tâm G. Gọi M, N, P lần lượt là trung điểm của các cạnh AB, BC, CA. Phép vị tự nào sau đây biến tam giác ABC thành tam giác NPM?
A. V A ; - 1 2
B. V G ; 1 2
C. V G ; - 2
D. V G ; - 1 2
Cho tam giác ABCcó trọng tâm G. Gọi M, N, P lần lượt là trung điểm của các cạnh AB, BC, CA. Phép vị tự nào sau đây biến tam giác ABC thành tam giác NPM A.
V
A
;
−
1
2
.
B.
V
G
;
1
2...
Đọc tiếp
Cho tam giác ABCcó trọng tâm G. Gọi M, N, P lần lượt là trung điểm của các cạnh AB, BC, CA. Phép vị tự nào sau đây biến tam giác ABC thành tam giác NPM
A. V A ; − 1 2 .
B. V G ; 1 2 .
C. V G ; − 2 .
D. V G ; − 1 2 .
Cho tam giác ABC với trọng tâm G, trực tâm H và tâm đường tròn ngoại tiếp O. Phép vị tự
V
O
;
k
biến O thành H. Tìm k. A.
−
1
2
B. 2 C.
1
2
D. -2
Đọc tiếp
Cho tam giác ABC với trọng tâm G, trực tâm H và tâm đường tròn ngoại tiếp O. Phép vị tự V O ; k biến O thành H. Tìm k.
A. − 1 2
B. 2
C. 1 2
D. -2
Cho tam giác ABC, gọi H, G, O lần lượt là trực tâm, trọng tâm, tâm đường tròn ngoại tiếp của tam giác, M là trung điểm BC
a. CMR : AH = 2* OG
b> CMR : H, G, O thẳng hàng và GH= 2*OG
AI LÀM ĐÚNG MÌNH LIKE CHO
Cho tam giác ABC với trọng tâm G. Gọi ABC lần lượt là trung điểm của các cạnh BC, AC,AB của tam giác ABC. Phép vị tự biến tam giác ABC thành tam giác ABC là A. Phép vị tự tâm G, tỉ số k2 B. Phép vị tự tâm G, tỉ số k2 C. Phép vị tự tâm G, tỉ số k-3 D. Phép vị tự tâm G, tỉ số k3
Đọc tiếp
Cho tam giác ABC với trọng tâm G. Gọi A'B'C' lần lượt là trung điểm của các cạnh BC, AC,AB của tam giác ABC. Phép vị tự biến tam giác A'B'C' thành tam giác ABC là
A. Phép vị tự tâm G, tỉ số k=2
B. Phép vị tự tâm G, tỉ số k=2
C. Phép vị tự tâm G, tỉ số k=-3
D. Phép vị tự tâm G, tỉ số k=3
Đáp án B
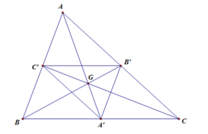
G A → = − 2 G A ' → ⇒ V G , − 2 A ' = A G B → = − 2 G B ' → ⇒ V G , − 2 B ' = B G C → = − 2 G C ' → ⇒ V G , − 2 C ' = C ⇒ V G , − 2 Δ A ' B ' C ' = Δ A B C
Đúng 0
Bình luận (0)
17 tháng 11 2019 lúc 10:51
Một số bài toán hay về tâm nội tiếp:Bài 1: Cho tam giác ABC nội tiếp (O), hai điểm K,L di chuyển trên (O) (K thuộc cung AB không chứa C, L thuộc cung AC không chứa B) thỏa mãn KL song song với BC. Gọi U và V lần lượt là tâm nội tiếp các tam giác AKB,ALC. Chứng minh rằng tâm của (UAV) thuộc đường thẳng cố định.Bài 2: Cho tứ giác lồi ABCD có AD BC. AC cắt BD tại I. Gọi S,T là tâm nội tiếp các tam giác AID,BIC. M,N là trung điểm các cạnh AB,CD. Chứng minh rằng MN chia đôi ST.Bài 3: Cho tam giác AB...
Đọc tiếp
Một số bài toán hay về tâm nội tiếp:
Bài 1: Cho tam giác ABC nội tiếp (O), hai điểm K,L di chuyển trên (O) (K thuộc cung AB không chứa C, L thuộc cung AC không chứa B) thỏa mãn KL song song với BC. Gọi U và V lần lượt là tâm nội tiếp các tam giác AKB,ALC. Chứng minh rằng tâm của (UAV) thuộc đường thẳng cố định.
Bài 2: Cho tứ giác lồi ABCD có AD = BC. AC cắt BD tại I. Gọi S,T là tâm nội tiếp các tam giác AID,BIC. M,N là trung điểm các cạnh AB,CD. Chứng minh rằng MN chia đôi ST.
Bài 3: Cho tam giác ABC, đường tròn (I) nội tiếp tam giác ABC tiếp xúc BC,CA,AB tại D,E,F. Kẻ DH vuông góc EF tại H, G là trung điểm DH. Gọi K là trực tâm tam giác BIC. Chứng minh rằng GK chia đôi EF.
Bài 4: Cho tam giác ABC ngoại tiếp (I), (I) tiếp xúc với BC,CA,AB tại D,E,F. Gọi AI cắt DE,DF tại K,L; H là chân đường cao hạ từ A của tam giác ABC, M là trung điểm BC. Chứng minh rằng bốn điểm H,K,L,M cùng thuộc một đường tròn có tâm nằm trên (Euler) của tam giác ABC.
chị gisp em bài này