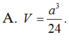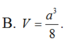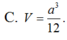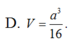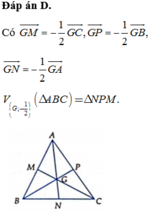Các câu hỏi tương tự
Cho hình chóp S.ABC có đáy là tam giác vuông cân ở B, ACa
2
, SA
⊥
(ABC), SAa. Gọi G là trọng tâm tam giác SBC, mặt phẳng (
α
) đi qua AG và song song với BC cắt SB, SC lần lượt tại M, N. Tính thể tích V của khối chóp S.AMN.
Đọc tiếp
Cho hình chóp S.ABC có đáy là tam giác vuông cân ở B, AC=a 2 , SA ⊥ (ABC), SA=a. Gọi G là trọng tâm tam giác SBC, mặt phẳng ( α ) đi qua AG và song song với BC cắt SB, SC lần lượt tại M, N. Tính thể tích V của khối chóp S.AMN.
![]()
![]()
![]()
![]()
Cho tam giác ABC. Gọi B’, C’ lần lượt là trung điểm của AB và AC. Tam giác ABC biến thành tam giác AB’C’ qua phép vị tự nào? A.
V
A
;
2
B.
V
A
;
1
2
C.
V
A
;...
Đọc tiếp
Cho tam giác ABC. Gọi B’, C’ lần lượt là trung điểm của AB và AC. Tam giác ABC biến thành tam giác AB’C’ qua phép vị tự nào?
A. V A ; 2
B. V A ; 1 2
C. V A ; − 2
D. V A ; − 1 2
Trong không gian Oxyz, cho tam giác ABC có tọa độ các điểm là: A(
x
A
;
y
A
,
z
A
), B(
x
B
;
y
B
,
z
B
), C(
x
C
;
y
C...
Đọc tiếp
Trong không gian Oxyz, cho tam giác ABC có tọa độ các điểm là: A( x A ; y A , z A ), B( x B ; y B , z B ), C( x C ; y C , z C ). Gọi M là trung điểm của BC, G là trọng tâm tam giác ABC. Khẳng định nào sau đây là sai?
A. M x B + x C 2 ; y B + y C 2 ; z B + z C 2
B. AB → = x B - x A ; y B - y A ; z B - z A
C. G x A + x B + x C 3 ; y A + y B + y C 3 ; z A + z B + z C 3
D. AB = ( x B - x A ) 2 ; y B - y A 2 ; ( z B - z A ) 2
Trong mặt phẳng Oxy, gọi các điểm M, N lần lượt là điểm biểu diễn số phức
z
1
2
-
i
,
z
2
1
+
4
i
Gọi G là trọng tâm của tam giác OMN, với O là gốc tọa độ. Hỏi G là điểm biểu diễn của số phức nào sau đây?
Đọc tiếp
Trong mặt phẳng Oxy, gọi các điểm M, N lần lượt là điểm biểu diễn số phức z 1 = 2 - i , z 2 = 1 + 4 i Gọi G là trọng tâm của tam giác OMN, với O là gốc tọa độ. Hỏi G là điểm biểu diễn của số phức nào sau đây?
![]()
![]()
![]()
![]()
Gọi A,B,C lần lượt là điểm biểu diễn hình học của các số phức z11-2i, z2-1+i và z33+4i. Điểm G trọng tâm tam giác ABC là điểm biểu diễn của số phức nào sau đây? A.z1-i. B.z3+3i. C.z1+2i. D.z1+i
Đọc tiếp
Gọi A,B,C lần lượt là điểm biểu diễn hình học của các số phức z1=1-2i, z2=-1+i và z3=3+4i. Điểm G trọng tâm tam giác ABC là điểm biểu diễn của số phức nào sau đây?
A.z=1-i.
B.z=3+3i.
C.z=1+2i.
D.z=1+i
Cho các số phức
z
1
1
;
z
2
2
+
2
i
;
z
3
-
1
+
3
i
được biểu diễn trong mặt phẳn...
Đọc tiếp
Cho các số phức z 1 = 1 ; z 2 = 2 + 2 i ; z 3 = - 1 + 3 i được biểu diễn trong mặt phẳng tọa độ Oxy là M,N,P, các điểm này lần lượt là trung điểm của ba cạnh tam giác EFH. Tọa độ trọng tâm G của tam giác EFH là:
A. (2;3)
B. (3;2)
C. 2 3 ; 2 3
D. 2 3 ; 5 3
Cho tứ diện đều ABCD cạnh a. Gọi M,N,G lần lượt là trung điểm của các cạnh AB, BC và trọng tâm tam giác ACD. Diện tích của thiết diện khi cắt tứ diện bởi mặt phẳng (MNG) bằng
Đọc tiếp
Cho tứ diện đều ABCD cạnh a. Gọi M,N,G lần lượt là trung điểm của các cạnh AB, BC và trọng tâm tam giác ACD. Diện tích của thiết diện khi cắt tứ diện bởi mặt phẳng (MNG) bằng
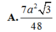
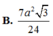
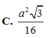
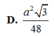
Cho hình chóp S.ABC có đáy là tam giác vuông cân tại B, AC a
2
, biết SA vuông góc với mặt đáy, SA a. Gọi G là trọng tâm của tam giác SBC, là mặt phẳng đi qua AG và song song với BC cắt SB, SC lần lượt tại M và N. Tính thể tích V của khối đa diện AMNBC. A. V
4
9
a
3
B. V
2
27
a
3
C. V
5...
Đọc tiếp
Cho hình chóp S.ABC có đáy là tam giác vuông cân tại B, AC = a 2 , biết SA vuông góc với mặt đáy, SA = a. Gọi G là trọng tâm của tam giác SBC, là mặt phẳng đi qua AG và song song với BC cắt SB, SC lần lượt tại M và N. Tính thể tích V của khối đa diện AMNBC.
A. V = 4 9 a 3
B. V = 2 27 a 3
C. V = 5 27 a 3
D. V = 5 54 a 3
Cho hình lăng trụ
A
B
C
.
A
B
C
có thể tích bằng
a
3
. Gọi M, N, P lần lượt là tâm của các mặt bên và G là trọng tâm tam giác ABC . Tính thể tích V của khối tứ diện GMNP.
Đọc tiếp
Cho hình lăng trụ A B C . A ' B ' C ' có thể tích bằng a 3 . Gọi M, N, P lần lượt là tâm của các mặt bên và G là trọng tâm tam giác ABC . Tính thể tích V của khối tứ diện GMNP.