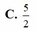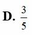Chọn D.
M(1;0), N(2;2), P(-1;3) là điểm biểu diễn các số phức trên .
Hai tam giác EFH và MNP có 3 trung tuyến trùng nhau từng đôi một nên có cùng trọng tâm G.
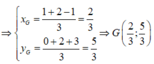
Chọn D.
M(1;0), N(2;2), P(-1;3) là điểm biểu diễn các số phức trên .
Hai tam giác EFH và MNP có 3 trung tuyến trùng nhau từng đôi một nên có cùng trọng tâm G.
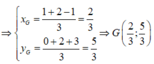
Trên mặt phẳng tọa độ, các điểm A, B, C theo thứ tự biểu diễn các số phức 2+3i, 3+i, 1+2i.Trọng tâm G của tam giác ABC biểu diễn số phức z. Tìm z
A. z=1+i
B.z=2+2i
C.z=2-2i
D.z=1-i
Trong mặt phẳng Oxy, gọi các điểm M, N lần lượt là điểm biểu diễn số phức z 1 = 2 - i , z 2 = 1 + 4 i Gọi G là trọng tâm của tam giác OMN, với O là gốc tọa độ. Hỏi G là điểm biểu diễn của số phức nào sau đây?
![]()
![]()
![]()
![]()
Trong mặt phẳng tọa độ Oxy, cho điểm M, N, P lần lượt là điểm biểu diễn của các số phức 2 + 3 i ; 1 - 2 i ; - 3 + i Tọa độ điểm Q sao cho tứ giác MNPQ là hình bình hành là
![]()
![]()
![]()
![]()
Cho số phức z = 1 + 3 i . Gọi A,B lần lượt là điểm biểu diễn của các số phức (1+i)z và (3-i)z trong mặt phẳng tọa độ Oxy. Tính độ dài đoạn AB.
![]()
![]()
![]()
![]()
Cho các số phức z1=3-2i, z2=1+4i và z3=-1+i có biểu diễn hình học trong mặt phẳng tọa độ Oxy lần lượt là các điểm A,B,C. Diện tích tam giác ABC bằng:
A.![]() .
.
B.12.
C.![]() .
.
D.9.
Trong mặt phẳng Oxy, gọi A là điểm biểu diễn số phức z thỏa mãn:\(\left(1-2i\right)z-\dfrac{2-i}{1+i}=\left(3-i\right)z\) . Tọa độ trung điểm I của OA là
A: I \(\left(\dfrac{1}{20};\dfrac{7}{20}\right)\)
B: I \(\left(\dfrac{1}{5};\dfrac{7}{5}\right)\)
C:I \(\left(\dfrac{1}{10};\dfrac{7}{10}\right)\)
D:I \(\left(\dfrac{1}{16};\dfrac{7}{16}\right)\)
Trong mặt phẳng Oxy gọi A,B,C lần lượt là các điểm biểu diễn số phức z1=-3i,z2=2-2i,z3=-5-i. Gọi G là trọng tâm của tam giác ABC. Khi đó điểm G biểu diễn số phức
A. z=-1-i
B.z=-1-2i
C.z=1-2i
D.z=2-i
Cho số phức z thỏa mãn iz + 2 - i = 0. Khoảng cách từ điểm biểu diễn của z trên mặt phẳng tọa độ Oxy đến điểm M(3;-4) là:
A. 2 5
B. 13
C. 2 10
D. 2 2
Trong mặt phẳng tọa độ Oxy, gọi M là điểm biểu diễn số phức z = 1 - 2 i , N là điểm biểu diễn số phức z ' ¯ = 1 - i 2 z . Tính diện tích tam giác OMM′.
![]()