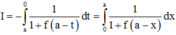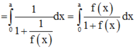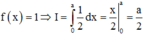f(x)^3 + f(x)= x
Tính tích phân f(x)dx từ 0 đến 2
f(x)^3 + f(x)= x Tính tích phân f(x)dx từ 0 đến 2
Cho hai hàm số liên tục f(x) và g(x) có nguyên hàm lần lượt là F(x) và G(x) trên [0; 2]. Biết F(0) = 0, F(2) = 1, G(2) = 1 và ∫ 0 2 F ( x ) g ( x ) d x = 3 . Tính tích phân hàm: ∫ 0 2 G ( x ) f ( x ) d x
A. I = 3.
B. I = 0.
C. I = -2.
D. I = -4.
Chọn C.
Đặt u = G ( x ) d v = f ( x ) d x ⇒ d u = G ( x ) ' d x = g ( x ) d x v = ∫ f ( x ) d x = F ( x )
Suy ra: I = G ( x ) F ( x ) 2 0 - ∫ 0 2 F ( x ) g ( x ) d x
= G(2)F(2) – G(0)F(0) – 3 = 1 – 0 – 3 = -2.
Cho hàm số f(x) thỏa mãn ∫ 0 1 ( x + 1 ) f ' ( x ) d x = 10 và 2f(1) - f(0) = 2 .Tính tích phân I = ∫ 0 1 f ( x ) d x .
A. I=-12.
B. I=8.
C. I=12.
D. I=-8
Cho hàm số f (x) có đạo hàm liên tục trên đoạn [1;2] thỏa mãn ∫ 1 2 ( x - 1 ) 2 f ( x ) d x = - 1 3 , f(2) = 0 và ∫ 1 2 f ' ( x ) 2 d x = 7 . Tính tích phân ∫ 1 2 f ( x ) d x
A. I = 7 5
B. I = - 7 5
C. I = - 7 20
D. I = 7 20
Cho hàm số y=f(x) có đạo hàm liên tục trên đoạn [ 0 ; 2 ] và thỏa mãn f ( 0 ) = 2 , ∫ 0 2 ( 2 x - 4 ) . f ' ( x ) d x = 4 . Tính tích phân I = ∫ 0 2 f ( x ) d x .
A. I = 2
B. I = - 2
C. I = 6
D. I = - 6
Cho hàm số f(x) có đạo hàm liên tục trên 0 ; π 2 thỏa mãn f ( 0 ) = 0 ; ∫ 0 π 2 f ' ( x ) 2 d x = π 4 ; ∫ 0 π 2 sin x . f ( x ) d x = π 4 Tính tích phân ∫ 0 π 2 f ( x ) d x
A. 1
B. π 2
C. 2
D. π 4
Cho hàm số f(x) liên tục trên R, và các tích phân ∫ 0 π 2 f ' ( x ) d x = π 4 , ∫ 0 π 2 sin x f ( x ) d x = π 4 . Biết rằng f(0)=0 , tính f π 3
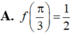
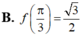
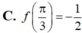
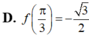
Cho hàm số f(x) thỏa mãn f'(x)=2f(x), ∀ x ∈ R và f(0)= 3 . Tích phân ∫ 0 1 f ( x ) d x bằng
A. 2 3 e 2 - 1
B. 3 2 e - 1
C. 3 e 2 - 1 2
D. 3 2 e - 1 2
Cho số thực a>0. Giả sử hàm số f(x) liên tục và luôn dương trên đoạn [0;a] thỏa mãn f(x).f(a – x) = 1, ∀ x ∈ [0;a]. Tính tích phân I = ∫ 0 a 1 1 + f ( x ) d x
Đáp án A
Phương pháp : Sử dụng phương pháp đổi biến, đặt x = a – t.
Cách giải : Đặt x = a – t => dx = –dt. Đổi cận 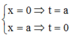
=>