trong mặt phẳng Oxy,ảnh của đường tròn: (x-2)^2 + (y-1)^2=16 qua phép tịnh tiến theo vescto v=(1;3) là đường tròn có phương trình

Những câu hỏi liên quan
Câu 1: trong mặt phẳng Oxy,ảnh của đường tròn: (x-2)^2 + (y-1)^2=16 qua phép tịnh tiến theo vescto v=(1;3) là đường tròn có phương trình như thế nào ?
Câu 2: trong mặt phẳng Oxy cho 2 điểm A(1;6);B(-1;-4).gọi C,D lần lược là ảnh của A và B qua phép tịnh tiến theo vécto v= (1;5).tìm và khẳng định
câu 1 : bài này có thể giải với nhiều loại cách khác nhau ; giờ mk sẽ giải cho bn bài này với 2 cách .
\(cách_1:\) vì đường tròn \(\left(x-2\right)^2+\left(y-1\right)^2=16\) là ảnh của đường tròn cần tìm được tịnh tiến theo \(\overrightarrow{v}\left(1;3\right)\)
nên ta lấy ảnh của đường tròn này tịnh tiến với véc tơ đối của \(\overrightarrow{v}\) là xong
ta có : \(\overrightarrow{n}\left(-1;-3\right)=-\overrightarrow{v}\left(1;3\right)\)
theo công thức ta có \(\left\{{}\begin{matrix}x'=x-1\\y'=y-3\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}y=y'+1\\x=x'+3\end{matrix}\right.\)
\(\Rightarrow\left(x-2\right)^2+\left(y-1\right)^2=16\)
\(\Leftrightarrow\left(x'+1-2\right)^2+\left(y'+3-1\right)^2=16\)
\(\Leftrightarrow\left(x'-1\right)^2+\left(y'+2\right)^2=16\)
vậy đường tròn lúc đầu có phương trình \(\left(x-1\right)^2+\left(y+2\right)^2=16\)
\(cách_2:\)vì là ảnh nên \(x;y\) trong \(\left(x-2\right)^2+\left(y-1\right)^2=16\) là \(x';y'\) trong công thức .
theo công thức ta có : \(\left\{{}\begin{matrix}x'=x+1\\y'=y+3\end{matrix}\right.\)
\(\Rightarrow\left(x-2\right)^2+\left(y-1\right)^2=16\)
\(\Leftrightarrow\left(x+1-2\right)^2+\left(y+3-1\right)^2=16\)
\(\Leftrightarrow\left(x-1\right)^2+\left(y+2\right)^2=16\)
vậy đường tròn lúc đầu có phương trình \(\left(x-1\right)^2+\left(y+2\right)^2=16\)
(bn chú ý \(x;y\) và \(x';y'\) trong 2 cách làm là khác nhau nha ; mk có giải thích ở trên) .
câu 2 : với \(T_{\overrightarrow{v}}\left(A\right)\)
theo công thức ta có : \(\left\{{}\begin{matrix}x'=x+a\\y'=y+b\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x'=1+1=2\\y'=6+5=11\end{matrix}\right.\)
\(\Rightarrow C\left(2;11\right)\)
với \(T_{\overrightarrow{v}}\left(B\right)\)
theo công thức ta có : \(\left\{{}\begin{matrix}x'=x+a\\y'=y+b\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x'=-1+1=0\\y'=-4+5=1\end{matrix}\right.\)
\(\Rightarrow D\left(0;1\right)\)
vậy điểm \(C\left(2;11\right);D\left(0;1\right)\)
Đúng 0
Bình luận (1)
Trong mặt phẳng tọa độ Oxy ảnh của đường tròn (C)
x
+
1
2
+
(
y
-
3
)
2
4
qua phép tịnh tiến theo ve...
Đọc tiếp
Trong mặt phẳng tọa độ Oxy ảnh của đường tròn (C) x + 1 2 + ( y - 3 ) 2 = 4 qua phép tịnh tiến theo vectơ v → =(3;2) là đường tròn có phương trình:
A. x + 2 2 + ( y + 5 ) 2 = 4
B. x - 2 2 + ( y - 5 ) 2 = 4
C. x - 1 2 + ( y + 3 ) 2 = 4
D. x + 4 2 + ( y - 1 ) 2 = 4
Trong mặt phẳng Oxy, cho điểm A(1;2), B(2;4), C(−1;3) và đường thẳng (d) : x + y - 5 = 0 và đường tròn (C) : ((x - 2) ^ 2) + (y + 1) ^ 2 = 4 . a. Tìm ảnh của vec A qua phép tịnh tiến theo vec v = (3; 1) . b. Tìm đường thẳng (d') là ảnh của đường thẳng (d) qua phép tịnh tiến theo a = 3i - 2j C. Tìm đường tròn (C') là ảnh của đường tròn (C) qua phép tịnh tiến theo AB . d. Tìm vec u, biết T vec u (B) = C
a: Ảnh của A là:
x=1+3=4 và y=2+1=3
b: (d') là ảnh của (d) qua phép tịnh tiến vecto a=(3;-2)
=>(d'): x+y+c=0
Lấy B(1;4) thuộc (d)
=>B'(4;2)
Thay x=4 và y=2 vào (d'), ta được:
c+4+2=0
=>c=-6
d: Theo đề,ta có:
2+x=-1 và 4+y=3
=>x=-3 và y=-1
=>vecto u=(-3;-1)
Đúng 0
Bình luận (0)
Trong mặt phẳng Oxy, cho đường thẳng d có phương trình x+y-10 và đường tròn (C):
(
x
-
3
)
2
+
(
y
-
1
)
2
1
. Ảnh của đường thẳng d qua phép tịnh tiến theo véc tơ
v
→
4
;
0
cắt đường tròn (C) tại hai điểm...
Đọc tiếp
Trong mặt phẳng Oxy, cho đường thẳng d có phương trình x+y-1=0 và đường tròn (C): ( x - 3 ) 2 + ( y - 1 ) 2 = 1 . Ảnh của đường thẳng d qua phép tịnh tiến theo véc tơ v → = 4 ; 0 cắt đường tròn (C) tại hai điểm A x 1 ; y 1 và B x 2 ; y 2 . Giá trị x 1 + x 2 bằng
A. 5
B. 8
C. 6
D. 7
Trong mặt phẳng Oxy cho pt (C) : (x+3)2 + (y-1)2 =5 và v = (-3;1) . Viết pt đường tròn (C’) biết (C’) là ảnh của (C) qua phép đồng dạng có được bằng thực hiện liên tiế phép tịnh tiến theo vecto V và phép vị tự tâm O tỷ số k= 2.
Trong mặt phẳng tọa độ Oxy ảnh của đường tròn
C
:
x
+
1
2
+
y
−
3
2
4
qua phép tịnh tiến theo vectơ
v
→
3
;
2...
Đọc tiếp
Trong mặt phẳng tọa độ Oxy ảnh của đường tròn C : x + 1 2 + y − 3 2 = 4 qua phép tịnh tiến theo vectơ v → = 3 ; 2 là đường tròn có phương trình:
A. x + 2 2 + y + 5 2 = 4
B. x − 2 2 + y − 5 2 = 4
C. x − 1 2 + y + 3 2 = 4
D. x + 4 2 + y − 1 2 = 4
Đáp án B.
Từ C : x + 1 2 + y − 3 2 = 4 có tâm I − 1 ; 3 và bán kính R=2.
V v → I = I ' 2 ; 5 nên có PT là x − 2 2 + y − 5 2 = 4 .
Đúng 0
Bình luận (0)
Trong mặt phẳng tọa độ Oxy ảnh của đường tròn
C
:
x
+
1
2
+
y
−
3
2
4
qua phép tịnh tiến theo vectơ
v
→
3
;
2...
Đọc tiếp
Trong mặt phẳng tọa độ Oxy ảnh của đường tròn C : x + 1 2 + y − 3 2 = 4 qua phép tịnh tiến theo vectơ v → = 3 ; 2 là đường tròn có phương trình:
A. x + 2 2 + y + 5 2 = 4
B. x − 2 2 + y − 5 2 = 4
C. x − 1 2 + y + 3 2 = 4
D. x + 4 2 + y − 1 2 = 4
Đáp án B.
Từ C : x + 1 2 + y − 3 2 = 4 có tâm I − 1 ; 3 và bán kính R=2 .
V v → I = I ' 2 ; 5 nên có PT là x − 2 2 + y − 5 2 = 4 .
Đúng 0
Bình luận (0)
Trong mặt phẳng tọa độ Oxy cho vectơ
v
→
-
1
;
2
,
A
3
;
5
,
B
-
1
;
1
và đường thẳng d có phương trình
x
–
2...
Đọc tiếp
Trong mặt phẳng tọa độ Oxy cho vectơ v → = - 1 ; 2 , A 3 ; 5 , B - 1 ; 1 và đường thẳng d có phương trình x – 2 y + 3 = 0 .
a. Tìm tọa độ của các điểm A' , B' theo thứ tự là ảnh của A, B qua phép tịnh tiến theo vecto v →
b. Tìm tọa độ của điểm C sao cho A là ảnh của C qua phép tịnh tiến theo vectơ v →
c. Tìm phương trình của đường thẳng d' là ảnh của d qua phép tịnh tiến theo v .
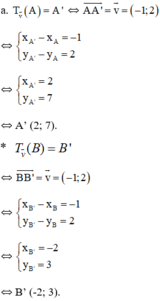
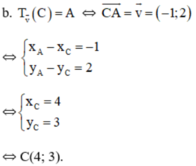
c) Đường thẳng d có vecto pháp tuyến là n→(1;-2) nên 1 vecto chỉ phương của d là(2; 1)
=> Vecto v→ không cùng phương với vecto chỉ phương của đường thẳng d
=> Qua phép tịnh tiến v→ biến đường thẳng d thành đường thẳng d’ song song với d.
Nên đường thẳng d’ có dạng : x- 2y + m= 0
Lại có B(-1; 1) d nên B’(-2;3) d’
Thay tọa độ điểm B’ vào phương trình d’ ta được:
-2 -2.3 +m =0 ⇔ m= 8
Vậy phương trình đường thẳng d’ là:x- 2y + 8 = 0
Đúng 0
Bình luận (0)
Trong mặt phẳng tọa độ Oxy cho điểm A(4; – 1), đường thẳng (d) : 3x – 2y + 1 = 0 và đường tròn (C) :
x^2 + y^2 - 2x + 4y -4 = 0
a. Tìm tọa độ A’ và phương trình (d’) lần lượt là ảnh của A và (d) qua phép tịnh tiến theo vectơ v = (– 2; 3)
b. Tìm phương trình đường tròn (C’) là ảnh của đường tròn (C) qua phép đối xứng trục là đường thẳng (D) : x – y = 0













