cho tam giác ABC trên BC lấy M bất kì . Trên AM lấy D bất kì . CMR: \(\dfrac{S_{ABD}}{S_{ACD}}=\dfrac{BM}{CM}\)

Những câu hỏi liên quan
cho tam giác abc ,m là điểm bất kì trên cạnh bc.c/m\(\frac{S_{ABM}}{S_{ACM}}=\frac{BM}{CM}\)
Cho tam giác ABC có M là trung điểm BC (BM = MC) và D là một điểm bất kì trên đoạn AM. Tính diện tích tam giác ABD biết diện tích tam giác ACD là 24cm2.
Cho tam giác ABC (AB<AC).Tia phân giác của góc A cắt BC ở D.Lấy M trên cạnh AC sao cho AB=AM a)Chứng minh rằng tam giác ABD=tam giác AMD b)cm DM<DC c)Lấy E bất kì trên AD cm BE=BM d) cm AC-AB>EC-EB
Cho tam giác ABC vuông tại A, đường cao AH. Lấy điểm K bất kỳ trên cạnh AC \(\left(K\ne A;K\ne C\right)\). Gọi D là hình chiếu của A trên BK. Chứng minh \(S_{BHD}=\dfrac{1}{4}S_{BKC}.cos^2\widehat{ABD}\)
Đề bài của em bị sai
Hai tam giác BHD và BKC đồng dạng do chung góc \(\widehat{KBC}\) và \(\widehat{BDH}=\widehat{BCK}\) (cùng bằng \(\widehat{BAH}\))
Do đó tỉ số đồng dạng 2 tam giác là \(k=\dfrac{BD}{BC}\)
\(\Rightarrow\dfrac{S_{BDH}}{S_{BKC}}=k^2=\dfrac{BD^2}{BC^2}\)
Nếu đề bài đúng thì đồng nghĩa ta phải chứng minh:
\(\dfrac{BD^2}{BC^2}=\dfrac{cos^2\widehat{ABD}}{4}=\dfrac{\left(\dfrac{BD}{AB}\right)^2}{4}=\dfrac{BD^2}{4AB^2}\)
\(\Rightarrow BC^2=4AB^2\) nhưng điều này rõ ràng ko đúng (vì đề bài ko hề cho BC=2AB)
Đúng 1
Bình luận (1)
Cho tam giác ABC đều nội tiếp (O) bán kính R lấy M bất kì trên cung nhỏ BC AM cắt BM tại I
1 cm ib.ic=ia.im
2 cm mi.ma=ac2
3 D thuộc AM sao cho AD=MC cm BD=BM
4 cm bm+mc=ma
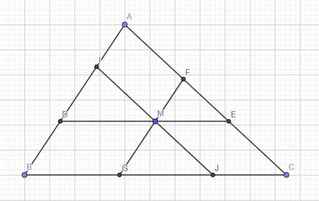
Cho điểm $M$ bất kì nằm trong $\Delta ABC$. Qua $M$ kẻ $DE//BC,FG//AB,IJ//AC$ với \((G,J\in BC;E,F\in AC;D,I\in AB)\)
Chứng minh rằng \(S_{AIMF}+S_{BGMD}+S_{CEMJ}\le \dfrac{2}{3}S_{ABC}\)
\(\left\{{}\begin{matrix}\widehat{MGJ}=\widehat{B}\left(\text{đồng vị}\right)\\\widehat{MJG}=\widehat{C}\left(\text{đồng vị}\right)\end{matrix}\right.\) \(\Rightarrow\Delta MGJ\sim\Delta ABC\) theo tỉ số \(k_1=\dfrac{GJ}{BC}\)
\(\Rightarrow S_{ABC}.k_1^2=S_{MGJ}\Rightarrow k_1=\sqrt{\dfrac{S_{MGJ}}{S_{ABC}}}=\dfrac{GJ}{BC}\) (1)
Tương tự: \(\dfrac{DM}{BC}=\sqrt{\dfrac{S_{IDM}}{S_{ABC}}}\), mà BDMG là hbh (2 cặp cạnh đối song song)
\(\Rightarrow DM=BG\Rightarrow\dfrac{BG}{BC}=\sqrt{\dfrac{S_{IDM}}{S_{ABC}}}\) (2)
Tương tự: \(\dfrac{CJ}{BC}=\sqrt{\dfrac{S_{FME}}{S_{ABC}}}\) (3)
Cộng vế (1);(2);(3) \(\Rightarrow\sqrt{\dfrac{S_{MGJ}}{S_{ABC}}}+\sqrt{\dfrac{S_{IDM}}{S_{ABC}}}+\sqrt{\dfrac{S_{FME}}{S_{ABC}}}=\dfrac{BG+GJ+JC}{BC}=1\)
\(\Rightarrow S_{ABC}=\left(\sqrt{S_{MGJ}}+\sqrt{S_{IDM}}+\sqrt{S_{FME}}\right)^2\le3\left(S_{MGJ}+S_{IDM}+S_{FME}\right)\)
Mà \(S_{MGJ}+S_{IDM}+S_{FME}=S_{ABC}-\left(S_{AIMF}+S_{BGMD}+S_{CEMJ}\right)\)
\(\Rightarrow S_{ABC}\le3\left[S_{ABC}-\left(S_{AIMF}+S_{BGMD}+S_{CEMJ}\right)\right]\)
\(\Rightarrow S_{AIMF}+S_{BGMD}+S_{CEMJ}\le\dfrac{2}{3}S_{ABC}\)
Đúng 3
Bình luận (0)
Cho tam giác ABC, M là điểm bất kì trên cạnh BC. Qua B và C kẻ đường thẳng song song với AM, cắt các đường thẳng AC và AB tương ứng tại E và D. CMR :\(\dfrac{1}{AM}=\dfrac{1}{BE}+\dfrac{1}{CD}\)
Xét ΔCBE có AM//BE
nên \(\dfrac{AM}{BE}=\dfrac{CM}{CB}\)
Xét ΔBDC có AM//DC
nên \(\dfrac{AM}{DC}=\dfrac{BM}{BC}\)
\(\dfrac{AM}{BE}+\dfrac{AM}{DC}=\dfrac{BM}{BC}+\dfrac{CM}{BC}\)
=>\(AM\left(\dfrac{1}{BE}+\dfrac{1}{DC}\right)=\dfrac{BC}{BC}=1\)
=>\(\dfrac{1}{AM}=\dfrac{1}{BE}+\dfrac{1}{CD}\)
Đúng 1
Bình luận (0)
Cho hình bình hành ABCD. Trên BC và CD lần lượt lấy hai điểm M và N sao cho: \(\dfrac{CN}{ND}=2.\dfrac{BM}{MC}\). Gọi P, Q theo thứ tự là giao điểm của AM, AN với BD. CMR: \(S_{\Delta AMN}=2.S_{\Delta APQ}\)
Cho tam giác có AB=10cm,AC=20cm.Tia phân giác của góc BAC cắt BC tại D. a)Tính BD/CD b) Trên cạnh AC lấy điểm M sao cho đoạn AM=5cm.Chứng minh tam giác AMB và tam giác ABC đồng dạng c) Nếu cho BC là 1 đơn vị cm bất kì,vậy tính BM được không
a: BD/CD=AB/AC=1/2
b: Xét ΔAMB và ΔABC có
AM/AB=AB/AC
góc MAB=góc BAC
=>ΔAMB đồng dạng với ΔABC
Đúng 0
Bình luận (0)