GT:ΔAMN cân tại A E ϵAM , FϵAN: AE=AF MF cắt EN tại O AO cắt MN tại K KL: 1) ΔAFN =ΔAFM 2)ΔMEN=ΔNFM 3)MON cân tại O 4)EF//MN 5)AO phân giác MAN 6) AK vuông góc MN

Những câu hỏi liên quan
Cho tam giác ABC cân tại A . Trên AB lấy E . Trên AC lấy F sao cho AE = AF . CMR : BC + EF < 2BF
1. cho hình vuông ABCD tại lấy điểm E thuộc BC . Tia AE cắt tia DC tại F . Đường vuông góc với AE tại A cắt tia CD . a) chứng minh tam giác AEP cân . b) chứng minh 1/AB ( mũ 2 ) = 1/AE ( mũ 2 ) + 1/AF ( mũ 2 )
~ Giúp mình với ~
a)Xét \(\Delta APD\) và \(\Delta AEB\) có:
\(\widehat{ADP}=\widehat{ABE}=90^o\)
AD = AB ( hvABCD)
\(\widehat{PAD}=\widehat{EAB}\) (cùng phụ \(\widehat{DAE}\))
=> \(\Delta APD\) = \(\Delta AEB\) (gcg)
=>AP=AE
mà \(\widehat{PAE}=90^o\left(gt\right)\)
=>\(\Delta APE\) vuông cân tại A
b) Xét \(\Delta APF\) vuông tại A có:
\(\dfrac{1}{AP^2}+\dfrac{1}{AF^2}=\dfrac{1}{AD^2}\) ( hệ thức lượng trong tam giác vuông )
mà AP=AE ; AD=AB
=>\(\dfrac{1}{AE^2}+\dfrac{1}{AF^2}=\dfrac{1}{AB^2}\)
Đúng 2
Bình luận (1)
cho tam giác ABC cân tại A . Trên AB lấy E ; trên AC lấy F sao cho AE = AF . chứng minh EF//BC
Chứng minh ED//BC ???
Đề bài bị thiếu à ?
Hình bạn tự vẽ nha, và đề bài cũng có chút sai sót, phải là EF//BC mới là đúng!
Giải chứng minh ED//BC:
Vì \(\Delta ABC\) cân tại A (gt) => \(\widehat{ABC}=\widehat{ACB}=\left(180^0-\widehat{A}\right):2\)
Vì AE = AF (gt) => \(\Delta AFE\) cân tại A => \(\widehat{AEF}=\widehat{AFE}=\left(180^0-\widehat{A}\right):2\)
=> \(\widehat{ABC}=\widehat{ACB}=\widehat{AEF}=\widehat{AFE}=\left(180^0-\widehat{A}\right):2\)
mà \(\widehat{AEF}\) và \(\widehat{ABC}\) ở vị trí đồng vị
=> DE//BC (đpcm)
hình miễn vẽ
giải:
ta có do tam giác ABC là tam giác cân nên gócB=gócC=[180*-góc A]/2
và do AE=AF[gt]nên tam giác AEFlà tam giác cân tại gócA
suy ra gócE=góc F =[180-gócA]/2
suy ra góc E = góc B
Mà hai góc này lại nằm ở vị trí hai góc đồng vị
suy ra FE//BC [đpcm]
Xem thêm câu trả lời
Cho tam giác ABC cân tại A. Trên AB lấy điểm E, trên AC lấy điểm F sao cho AE = AF. Chứng minh rằng : BC + EF < 2.BF
cho tam giác ABC cân tại A trên AB, AC lấy E,F sao cho AE=AF
CNR: BC+EF<2BF
cho tam giác ABC cân tại A, gọi M là trung điểm của BC.
B) Vẽ BE vuông góc với với AC tại E, CF vuông góv AB tại F. CM: AE=AF c) Trên tia AM lấy điểm K bất kì sao cho AM<AK CM: AC-AF>KF-KC
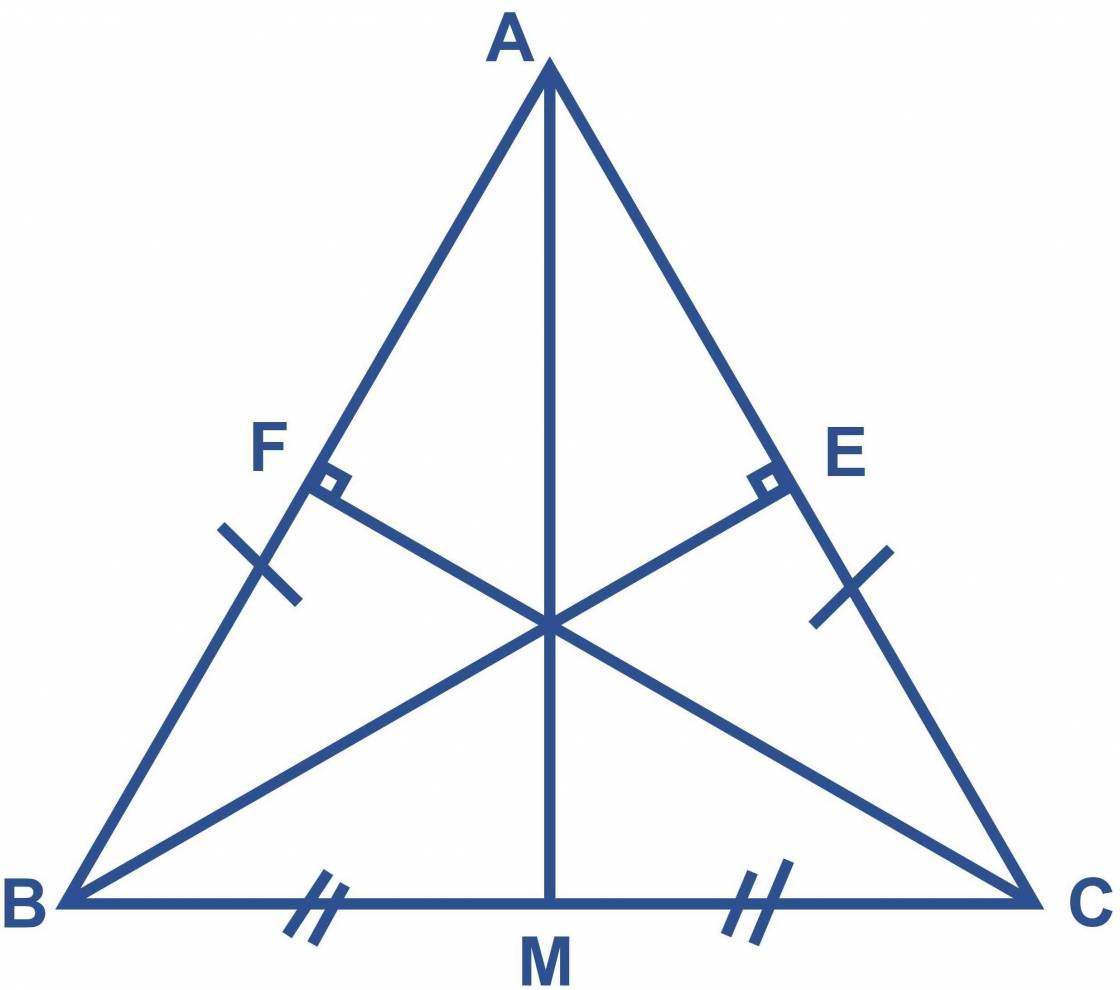
b) xét ΔBEA và ΔCFA, ta có :
AB = AC (2 cạnh bên của ΔABC cân tại A)
\(\widehat{A}\) là góc chung
=> ΔBEA = ΔCFA (ch-gn)
=> AE = AF (2 cạnh tương ứng)
Đúng 1
Bình luận (0)
Cho tam giác ABC cân tại A. Trên AB lấy điểm E, trên AC lấy điểm F sao cho AE = AF. Chứng minh rằng : BC + EF < 2.BF

mình chụp ảnh không biết bạn có hiểu không
Cho tam giác ABC vuông cân tại A (Â = 90°, AB = AC). Lấy E € AB
và Fe AC sao cho AE = AF. Đường thẳng đi qua A và vuông góc với BF cắt EC
tại M. Chứng minh rằng:
a) Chứng minh rằng ABAF = ACAE
b) Chứng minh rằng AEMA cân tại M,
c) Chứng minh rằng AAMC cân tại M. Từ đó, hãy suy ra ME = MC.
a: Xét ΔABF vuông tại A và ΔACE vuông tại E có
AB=AC
AF=AE
Do đó: ΔABF=ΔACE
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A, trên cạnh AB lấy điểm E, trên cạnh AC lấy điểm F sao cho AE=AF. chứng minh: BC+EF< 2 BC






















