Bài toán liên quan đến đường trung bình của tam giác, xin nhờ mọi người giúp đỡ với ạ!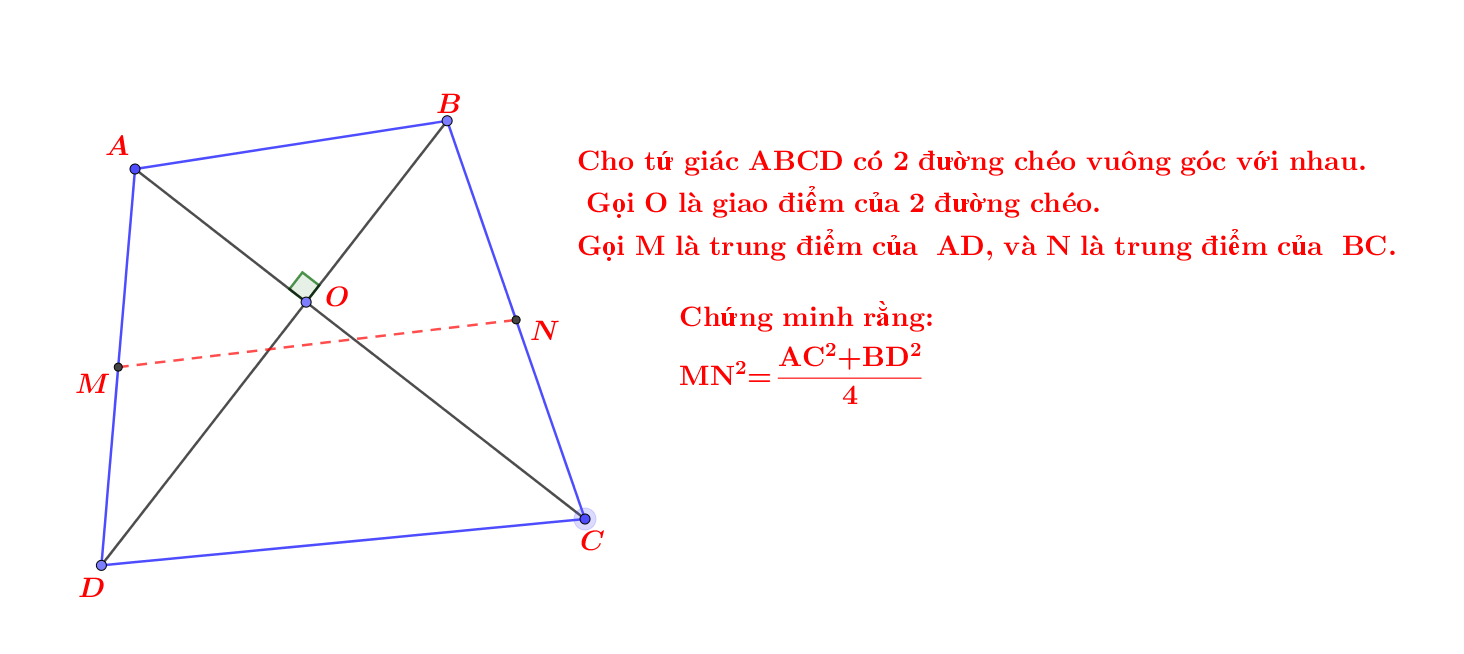

Những câu hỏi liên quan
cho tam giác ABC cân tại A ( góc A 90 độ ). kẻ các đường vuoonggosc với AB tại B, vuông góc với AC tại C, chúng cắt nhau tại I.a. chứng minh AI là phân giác góc BAC ( đã làm )b. gọi H lafhifnh chiếu của B trên AC. chứng minh CM // BI ( M là giao điểm của AI và BH )c. tam giác ABC cần có điều kiện gì để AB2AHLưu ý: Đề đúng, giúp mình ý b và c ( có thể thì giúp mình vẽ hình với tại câu b mình k biết vẽ hình )Mình sẽ tick những ai giúp mình làm bài. giải càng chi tiết càng nhiều phần thưởng ạ. Xin...
Đọc tiếp
cho tam giác ABC cân tại A ( góc A < 90 độ ). kẻ các đường vuoonggosc với AB tại B, vuông góc với AC tại C, chúng cắt nhau tại I.
a. chứng minh AI là phân giác góc BAC ( đã làm )
b. gọi H lafhifnh chiếu của B trên AC. chứng minh CM // BI ( M là giao điểm của AI và BH )
c. tam giác ABC cần có điều kiện gì để AB=2AH
Lưu ý: Đề đúng, giúp mình ý b và c ( có thể thì giúp mình vẽ hình với tại câu b mình k biết vẽ hình )
Mình sẽ tick những ai giúp mình làm bài. giải càng chi tiết càng nhiều phần thưởng ạ.
Xin vui lòng k bình luận k liên quan đến đề nhé. Mình xin cảm ơn trước, mình mới vào nên mongmn giúp đỡ nhiều hơn
MÌNH ĐANG CẦN GẤP LẮM Ạ!!!!!
hình bạn tự vẽ nhé
a. ví tam giác ABC là tam giác cân và có góc A bằng 90 độ nên tam giác ABC là tam giác vuông cân tại A
=> góc BAC = 90 độ và AB=AC
Xét tứ giác ABIC có góc BAC =90 độ, góc ABI = 90 độ (vì AIvuông góc với AB ), góc ACI =90độ (vì AC vuông góc với CI)
=> tứ giác ABIC là hình chữ nhật (dấu hiệu nhận biết hình chữ nhật)
mà AB=AC (cmt)
=> Tứ giác ABIC là hình vuông (dấu hiệu nhận biết hình vuông)
=> AI là phân giác góc BAC
mọi người giúp tớ bài này với ạ cho tam giác ABC nội tiếp đường tròn tâm O. gọi E,F Lần lượt là giao điểm của các tia phân giác trong va phân giác ngoài của hai góc B và C, đường thẳng EF cắt BC tại , cắt cung nhỏ BC ở M. chứng minha, ba điểm A,E,F thẳng hàngb, tứ giác BECF nội tiếp đường tròn tâm c, BI.ICIF.IE (BI nhân IC bằng IF nhân IE xin mọi người giúp tớ bài này với tớ xắp thi rồi ạ T T mong mọi người giúp đỡ *cúi*
Đọc tiếp
mọi người giúp tớ bài này với ạ
cho tam giác ABC nội tiếp đường tròn tâm O. gọi E,F Lần lượt là giao điểm của các tia phân giác trong va phân giác ngoài của hai góc B và C, đường thẳng EF cắt BC tại , cắt cung nhỏ BC ở M. chứng minh
a, ba điểm A,E,F thẳng hàng
b, tứ giác BECF nội tiếp đường tròn tâm
c, BI.IC=IF.IE (BI nhân IC bằng IF nhân IE
xin mọi người giúp tớ bài này với >< tớ xắp thi rồi ạ T T mong mọi người giúp đỡ *cúi*
Câu a mình làm xuống dưới nha =)))
b. Ta có, 2xgóc BCE + 2x góc BCF = 180° ( gt theo tia phân giác )
=> 2.(góc BCE + góc BCF ) = 180°
<=> góc ECF = 180°/ 2 = 90°
Chứng minh tương tự, có góc EBF = 90°
( từ hai điều trên ) suy ra góc ECF + góc EBF = 180°
=> tức giác BECF nội tiếp đường tròn có tâm là trung điểm của EF.
c, tức giác BECF nội tiếp => góc EBI = góc CIF
góc EIB = góc CIF ( đối đỉnh )
==> tam giác IEB đồng dạng với tam giác ICF
=> BI / IE = IF / IC
<=> BI.IC= IF.IE
a, trong tam giác ABC
có góc xBC = góc BAC + góc ACB ( góc ngoài tam giác )
=> 1/2 góc xBC = 1/2 góc BAC + 1/2 góc ACB
<=> FBI = góc EAC + góc ECA
mà EAC + ECA + AEC = 180°
==> góc FBI + góc AEC = 180° *
mà góc FBI = góc FEC ( tức giác BEFC nội tiếp ) **
Từ (*) và (**) suy ra FEC + AEC = 180°
=> E, F, A thẳng hàng.
Đúng 0
Bình luận (0)
A, xin lỗi, cái chỗ câu c nè
tức giác BECF nội tiếp suy ra góc EBI = góc CFI mới đúng nhé
xin lỗi, mình viết nhầm chỗ đó :(((
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Mọi người giúp em bài toán này với ạ. Em đang cần gấp. Em cảm ơn nhiều ạ
Bài: Cho tam giác ABC, M là trung điểm của BC. Lấy D đối xứng với với A qua M
a) Chứng tỏ ABCD là hình bình hành
b) Lấy E thuộc AB, F thuộc DC sao cho AE= DF. Chứng tỏ AEDF là hình bình hành
c) Chứng tỏ BECF là hình bình hành
d) Chứng tỏ E và F đối xứng nhau qua O
Cho tam giác ABC, H là trực tâm. Đường vuông góc với AC tại C và đường vuông góc với AB tại B cắt nhau tại D. Gọi O là trung điểm của AD, M là trung điểm của BC. Chứng minh rằng:
a, O là giao điểm cuả các đường trung trực tam giác ABC
b, OM = 1/2 AH
Xin mọi người giúp đỡ với, mai phải nộp bài rồi :(
Cho tam giác ABC, H là trực tâm. Đường vuông góc với AC tại C và đường vuông góc với AB tại B cắt nhau tại D. Gọi O là trung điểm của AD, M là trung điểm của BC. Chứng minh rằng:
a, O là giao điểm cuả các đường trung trực tam giác ABC
b, OM = 1/2 AH
Xin mọi người giúp đỡ với, mai phải nộp bài rồi :(
Cho m là đường trung trực của đoạn thẳng AB, C là điểm thuộc m. Gọi Cx là tia đối của tia CA, Cn là tia phân giác của góc BCx. Chứng minh rằng Cn vuông góc với m.
Nhờ mọi người giúp đỡ ạ *cúi đầu*
Xin nhờ quý thầy cô và các bạn yêu toán gần xa giúp đỡ với ạ!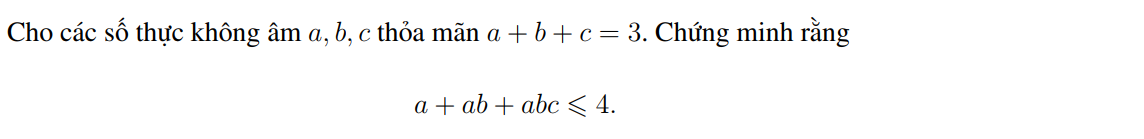
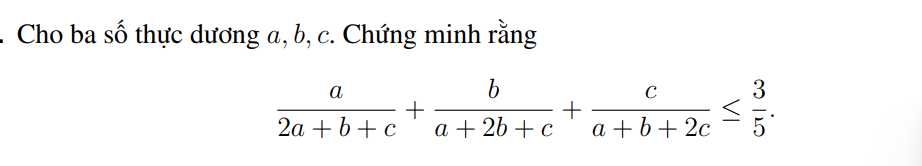
Áp dụng BĐT cosi dạng \(\dfrac{1}{a}+\dfrac{1}{b}\ge\dfrac{4}{a+b}\)
\(\Leftrightarrow\left(\dfrac{1}{a}+\dfrac{1}{b}\right)\cdot\dfrac{1}{4}\ge\dfrac{4}{a+b}\cdot\dfrac{1}{4}\\ \Leftrightarrow\dfrac{1}{a+b}\le\dfrac{1}{4}\left(\dfrac{1}{a}+\dfrac{1}{b}\right)\)
\(\Leftrightarrow\dfrac{a}{2a+b+c}=\dfrac{a}{a+b+a+c}\le\dfrac{a}{4}\left(\dfrac{1}{a+b}+\dfrac{1}{a+c}\right)\)
Cmtt \(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{b}{a+2b+c}\le\dfrac{b}{4}\left(\dfrac{1}{a+b}+\dfrac{1}{b+c}\right)\\\dfrac{c}{a+b+2c}\le\dfrac{c}{4}\left(\dfrac{1}{a+c}+\dfrac{1}{b+c}\right)\end{matrix}\right.\)
Cộng VTV 3 BĐT trên:
\(\Leftrightarrow VT\le\dfrac{1}{4}\left(\dfrac{a}{a+b}+\dfrac{a}{a+c}+\dfrac{b}{a+b}+\dfrac{b}{b+c}+\dfrac{c}{a+c}+\dfrac{c}{b+c}\right)\\ \Leftrightarrow VT\le\dfrac{1}{4}\left(\dfrac{a+b}{a+b}+\dfrac{b+c}{b+c}+\dfrac{a+c}{a+c}\right)=\dfrac{1}{4}\cdot3=\dfrac{3}{4}\)
Dấu \("="\Leftrightarrow a=b=c\)
Đúng 1
Bình luận (1)
Chứng minh rằng với mọi số nguyên dương \(n\) thì số \(A=59^n-17^n-9^n+2^n\) chia hết cho 35.
P/s: Em xin phép nhờ sự giúp đỡ của quý thầy cô giáo và các bạn yêu toán với ạ!
Em cám ơn nhiều lắm ạ!
Ta có: \(59\equiv3\left(mod7\right)\Rightarrow59^n\equiv3^n\left(mod7\right)\)
Tương tự: \(17^n\equiv3^n\left(mod7\right)\) ; \(9^n\equiv2^n\left(mod7\right)\)
\(\Rightarrow A\equiv3^n-3^n-2^n+2^n\left(mod7\right)\)
\(\Rightarrow A⋮7\)
Vẫn tương tự, ta có: \(A\equiv4^n-2^n-4^n+2^n\left(mod5\right)\)
\(\Rightarrow A⋮5\)
Mà 7 và 5 nguyên tố cùng nhau
\(\Rightarrow A⋮35\)
Đúng 1
Bình luận (0)
Cho tam giác ABc vuông cân tại A, lấy D thuộc AC, E thuộc AC sao cho AD = ASE. Các đường vuông góc với EC kẻ từ A và D lần lượt cắt BC ở K và L.
CM BK = KL
Xin nhờ mọi người giúp đỡ!











