Cho tam giác ABC cân, góc A=45o , AB=AC. I là trung điểm của AC.Từ I kẻ đường thẳng vuông góc với AC cắt đường thẳng BC ở M.N thuộc tia đối của AM, BM=AN. Chứng minh:
a) góc AMC = góc BAC
b) tam giác ABM = tam giác CAN
c) tam giác MNC vuông cân.
Những câu hỏi liên quan
cho tam giác ABC cân có góc A = 45 độ, AB = AC. Từ trung điểm I của cạnh AC kẻ đường thẳng vuông góc với AC cắt đường thẳng BC ở M.Trên tai đối tia Am lấy điểm N sao cho AN = BM. Chứng minh
a) Góc AMC = góc BAC
b) Tam giác ABM = tam giác CAN
c) Tam giác MNC vuông cân ở C
cho tam giác ABC cân có góc A = 45 độ, AB = AC. Từ trung điểm I của cạnh AC kẻ đường thẳng vuông góc với AC cắt đường thẳng BC ở M.Trên tai đối tia Am lấy điểm N sao cho AN = BM. Chứng minh
a) Góc AMC = góc BAC
b) Tam giác ABM = tam giác CAN
c) Tam giác MNC vuông cân ở C
cho tam giác cân ABC có góc A = 45 độ,AB=AC.từ trung điểm I của cạnh AC kẻ đường vuông góc vs AC cắt đường thẳng BC ở M.trên tia đối của tia AM lấy điểm N sao cho AN=BM. cmr:
a] góc AMC=góc ABC
b] tam giác ABM= tam giác CAN
c] tam giác MNC vuông cân ở C
cho tam giác cân ABC có góc A = 45 độ,AB=AC.từ trung điểm I của cạnh AC kẻ đường vuông góc vs AC cắt đường thẳng BC ở M.trên tia đối của tia AM lấy điểm N sao cho AN=BM. cmr:
a] góc AMC=góc ABC
b] tam giác ABM= tam giác CAN
c] tam giác MNC vuông cân ở C
http://olm.vn/hoi-dap/question/36403.html
Bạn copy link trên vào google và enter là được
Đúng 0
Bình luận (0)
cho tam giác cân ABC có góc A = 45 độ,AB=AC.từ trung điểm I của cạnh AC kẻ đường vuông góc vs AC cắt đường thẳng BC ở M.trên tia đối của tia AM lấy điểm N sao cho AN=BM. cmr:
a] góc AMC=góc ABC
b] tam giác ABM= tam giác CAN
c] tam giác MNC vuông cân ở C
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
cho tam giác ABC có góc A 45 độ , cạnh AB cạnh AC gọi I là trung điểm cạnh AC , qua I kẻ đường thẳng vuông góc với cạnh AC , cắt đường thảng BC ở M . Trên tia đôi tia AM lấy N sao cho AN BM a) góc AMC góc BACb ) tam giác ABM tam giác CANc ) tam giác MNC vuông cân ở C
Đọc tiếp
cho tam giác ABC có góc A = 45 độ , cạnh AB = cạnh AC gọi I là trung điểm cạnh AC , qua I kẻ đường thẳng vuông góc với cạnh AC , cắt đường thảng BC ở M . Trên tia đôi tia AM lấy N sao cho AN = BM
a) góc AMC = góc BAC
b ) tam giác ABM = tam giác CAN
c ) tam giác MNC vuông cân ở C
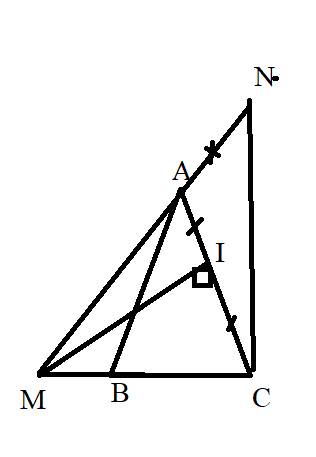
a: Xét ΔMAC có
MI là đường cao
MI là đường trung tuyến
Do đó: ΔMAC cân tại M
=>\(\widehat{AMC}=180^0-2\cdot\widehat{ACM}=180^0-2\cdot\widehat{ACB}\left(1\right)\)
ΔABC cân tại A
=>\(\widehat{BAC}=180^0-2\cdot\widehat{ACB}\left(2\right)\)
Từ (1) và (2) suy ra \(\widehat{AMC}=\widehat{BAC}\)
b:
ΔABC cân tại A
=>\(\widehat{ABC}=\widehat{ACB}\)
ΔMAC cân tại M
=>\(\widehat{MAC}=\widehat{MCA}=\widehat{ACB}\)
\(\widehat{ABM}+\widehat{ABC}=180^0\)(hai góc kề bù)
=>\(\widehat{ABM}=180^0-\widehat{ABC}=180^0-\widehat{ACB}\left(3\right)\)
\(\widehat{CAN}+\widehat{CAM}=180^0\)(hai góc kề bù)
=>\(\widehat{CAN}+\widehat{ACB}=180^0\)
=>\(\widehat{CAN}=180^0-\widehat{ACB}\left(4\right)\)
Từ (3) và (4) suy ra \(\widehat{ABM}=\widehat{CAN}\)
Xét ΔABM và ΔCAN có
AB=CA
\(\widehat{ABM}=\widehat{CAN}\)
BM=AN
Do đó;ΔABM=ΔCAN
c: ΔABM=ΔCAN
=>NC=MA
mà MA=MC
nên NC=MC
\(\widehat{AMC}=\widehat{BAC}\)
mà \(\widehat{BAC}=45^0\)
nên \(\widehat{AMC}=45^0\)
Xét ΔCMN có CM=CN và \(\widehat{CMN}=45^0\)
nên ΔCMN vuông cân tại C
Đúng 1
Bình luận (0)
Bài 1. Cho tam giác ABC cân tại A có BAC 45o. Từ trung điểm I của cạnh AC kẻ đường vuông góc với AC cắt đường thẳng BC tại M. Trên tia đối của tia AM lấy điểm N sao cho AN BM. Chứng minh:a) Chứng minh: ΔMAC cân.b) Chứng minh: AMC BAC 45oc) Chứng minh: ΔABM ΔCAN.d) Chứng minh: ΔMCN vuông cânBài 2. Cho ΔABC có góc A nhọn. Kẻ tia Ax ⊥ AB (tia AC nằm giữa Ax và AB ). Kẻ tia Ay ⊥ AC (tia AB nằm giữa Ay và AC). Lấy điểm E và F lần lượt thuộc tia Ax và Ay sao cho AE AB vàa) Chứng minh: BF CE.b)...
Đọc tiếp
Bài 1. Cho tam giác ABC cân tại A có BAC = 45o. Từ trung điểm I của cạnh AC kẻ đường vuông góc với AC cắt đường thẳng BC tại M. Trên tia đối của tia AM lấy điểm N sao cho AN = BM. Chứng minh:
a) Chứng minh: ΔMAC cân.
b) Chứng minh: AMC = BAC = 45o
c) Chứng minh: ΔABM = ΔCAN.
d) Chứng minh: ΔMCN vuông cân
Bài 2. Cho ΔABC có góc A nhọn. Kẻ tia Ax ⊥ AB (tia AC nằm giữa Ax và AB ). Kẻ tia Ay ⊥ AC (tia AB nằm giữa Ay và AC). Lấy điểm E và F lần lượt thuộc tia Ax và Ay sao cho AE = AB và
a) Chứng minh: BF = CE.
b) Gọi M và N lần lượt là trung điểm của BF và CE. Chứng minh: ΔAMN vuông cân.
Bài 3. Trên cạnh BC của ΔABC lấy 2 điểm E và F sao cho BE = CF. Qua E và F vẽ các đường thẳng song song với BA chúng cắt cạnh AC tại G và H. Qua E vẽ đường thẳng song song với AC cắt AB tại D.
a) Chứng minh: AD = GE.
b) Chứng minh: ΔBDE = ΔFHC.
c) Chứng minh: AB = GE + FH.
Bài 4. Cho tam giác ABC vuông tại A và AB = 2AC. Gọi E là trung điểm của AB. Trên tia đối của tia AC lấy điểm D sao cho AB = AD. Chứng minh rằng:
a) BC = DE.
b) BC ⊥ DE.
Bài 5. Cho ΔABC vuông cân tại A, M là trung điểm cạnh BC, E là điểm nằm giữa M và C. Vẽ BH ⊥ AE tại H và CK ⊥ AE tại K. CMR:
a) AM ⊥ BC
b) BH = AK
c) ΔMBH = ΔMAK
d) ΔMHK vuông cân.
Bài 4:
a) Ta có: AB=2AC(gt)
mà AB=2AE(E là trung điểm của AB)
nên AC=AE
Xét ΔBAC vuông tại A và ΔDAE vuông tại A có
BA=DA(gt)
AC=AE(gt)
Do đó: ΔBAC=ΔDAE(hai cạnh góc vuông)
Suy ra: BC=DE(hai cạnh tương ứng)
Bài 5:
a) Ta có: ΔABC vuông cân tại A(gt)
mà AM là đường trung tuyến ứng với cạnh đáy BC(M là trung điểm của BC)
nên AM là đường cao ứng với cạnh BC(Định lí tam giác cân)
⇒AM⊥BC(đpcm)
Đúng 1
Bình luận (0)
Cho tam giác ABC có góc A=45°, AB=AC. Từ trung điểm I của cạnh AC, kẻ đường vuông góc với AC cắt đường thẳng BC ở M. Trên tia đối của tia AM lấy điểm N sao cho AN=BM
a) góc AMC = góc ABC
b) tam giác ABM = tam giác CAM
c) tam giác MNC vuông cân ở C
Cho tam giác ABC cân có góc A = 45 độ, AB = AC. Từ trung điểm I của cạnh AC kẻ đường thẳng vuông góc với AC cắt đường thẳng BC ở M.Trên tai đối tia Am lấy điểm N sao cho AN = BM. Chứng minh
a) Góc AMC = góc BAC
b) Tam giác ABM = tam giác CAN
c) Tam giác MNC vuông ở C
nêu bạn thuc su muon giup thi vẽ hinh to se giup
Đúng 0
Bình luận (0)
cho tam giác ABC cân , có góc A = 45 độ , AB = AC từ chung điểm I của cạnh AC kẻ đường vuông góc với AC cắt đường thẳng BC ở M . trên tia đối của tia AM lấy điểm N sao cho AN = BM . CMR
a] góc AMC = góc ABC
b] tam giác ABM = tam giác CAN
c] tam giác MNC la giác CÂN ở C