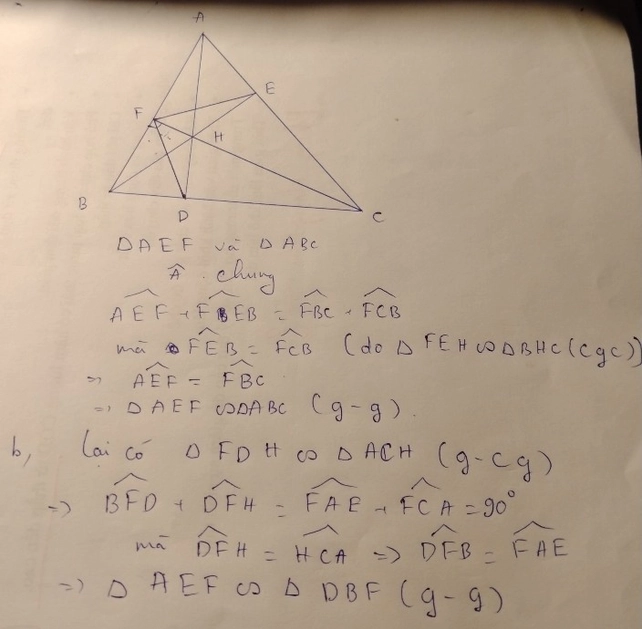2 góc đồi dỉnh trong tam giác đồng dạng có bằng nhau ko

Những câu hỏi liên quan
Tam giác ABC nhọn có AB<AC, góc A bằng 45 độ, các đường cao BD,CE cắt nhau tại H.
a. Chứng minh tam giác HED đồng dạng với tam giác HBC
b. Chứng minh tam giác AED đồng dạng với tam giác ABC
c. Tính DE khi BC bằng căn bậc 2
a. -Xét △BEH và △CDH có:
\(\widehat{BEH}=\widehat{CDH}=90^0\)
\(\widehat{BHE}=\widehat{CHD}\)(đối đỉnh)
\(\Rightarrow\)△BEH∼△CDH (g-g).
\(\Rightarrow\dfrac{BH}{CH}=\dfrac{EH}{DH}\).
-Xét △HED và △HBC có:
\(\widehat{EHD}=\widehat{BHC}\) (đối đỉnh)
\(\dfrac{BH}{CH}=\dfrac{EH}{DH}\left(cmt\right)\)
\(\Rightarrow\)△HED∼△HBC (c-g-c).
b. -Ta có: \(\widehat{AED}+\widehat{DEC}=90^0\) (kề phụ).
\(\widehat{DBC}+\widehat{DCB}=90^0\) (△DBC vuông tại D).
Mà \(\widehat{DEC}=\widehat{DBC}\)(△HED∼△HBC)
\(\Rightarrow\)\(\widehat{AED}=\widehat{DCB}\)
-Xét △AED và △ACB có:
\(\widehat{AED}=\widehat{ACB}\) (cmt)
\(\widehat{BAC}\) là góc chung.
\(\Rightarrow\)△AED∼△ACB (g-g).
Đúng 1
Bình luận (0)
c. -Có: \(\widehat{EAC}=45^0\) (gt) ; △AEC vuông tại E (AB⊥CE tại E).
\(\Rightarrow\)△AEC vuông cân tại E.
\(\Rightarrow AE=AC\sqrt{2}\)
-Ta có: △AED∼△ACB (cmt)
\(\Rightarrow\dfrac{ED}{BC}=\dfrac{AE}{AC}=\dfrac{AC\sqrt{2}}{AC}=\sqrt{2}\)
\(\Rightarrow\dfrac{ED}{\sqrt{2}}=\sqrt{2}\)
\(\Rightarrow ED=2\)
Đúng 0
Bình luận (1)
trên một cạnh của một góc có dỉnh la A dặt đoạn thẳng AE=3cm và AC=8cm.trên cạnh thứ hai của góc đó đặt các cạnh AD=4cm và AF=6cm.
a)hỏi tam giác ACD vtam giác AEF có đồng dạng với nhau không? vì sao?
b)gọi I là giao điểm của CD và EF tính tỷ số diện tích của hai tam giac IDF và IEC?
Cho tam giác ABC có AB:AC:CB = 2:3:4 và chu vi bằng 54 cm. Tam giác DEF có DE = 3 cm, DF = 4,5 cm, EF = 6 cm.
a) Tam giác ABC và DEF có đồng dạng với nhau ko? Vì sao?
b) Biết góc A = 105 độ, góc E = 45 độ. Tính các góc còn lại của mỗi tam giác.
a, 2 tam giác đồng dạng
CM:
xét tam giác ta có: \(2x+3x+4x=56\)(\(x\)là hệ số sao cho \(2x;3x;4x\)là ba cạnh của tam giác ABC)
=) \(x=6\)
tỉ lệ cạnh thì cậu chứng minh đc 2 tam giác đồng dạng nhé
b,vì hai tam đồng dạng nên
\(\widehat{ABC}=\widehat{DEF}=45^O\)
\(\widehat{BAC}=\widehat{EDF}=105^O\)
tổng 3 góc trong tam giác =180o
thì tính đc \(\widehat{ACB}=\widehat{DFE}=30^O\)
sao khi ra x=6 nhân vào 2x=2.6=12=AB
3x=3.6=18=AC
BC=4x=4.6=24
tỉ lệ cạnh \(\frac{AB}{DE}=\frac{AC}{DF}=\frac{BC}{EF}\)
hay \(\frac{12}{3}=\frac{18}{4,5}=\frac{24}{6}\)
2 tam giác bằng nhau có đồng dạng không ngược lại hai tam giác đồng dạng có bằng nhau không vì sao
Hai tam giác bằng nhau thì đồng dạng
Hai tam giác đồng dạng thì chưa chắc bằng nhau
Đúng 0
Bình luận (1)
nếu hai tam giác đồng dạng với nhau thì chúng có bằng nhau hay ko ? hãy nêu các trường hợp đồng dang của tam giác .
- Có
- Các trường hợp là :
đồng dạng (c.c.c) , đồng dạng (g.g) , đông dạng (c.g.c)
Tam giác đồng dạng có hai tính chất quan trọng sau đây: Ba cặp góc bằng nhau∠A=∠A′, ∠B=∠B′, ∠C=∠C′
Ba cặp cạnh tỉ lệ với nhauABA′B′=BCB′C′=CAC′A′
Đúng 0
Bình luận (0)
đồng dạng (c.c.c) , đồng dạng (g.g) , đồng dạng (c.g.c)

Tam giác đồng dạng có hai tính chất quan trọng sau đây: Ba cặp góc bằng nhau∠A=∠A′, ∠B=∠B′, ∠C=∠C′
Ba cặp cạnh tỉ lệ với nhauABA′B′=BCB′C′=CAC′A′
Vậy làm thế nào để chứng minh hai tam giác là đồng dạng với nhau. Thông thường chúng ta có ba cách sau đây.
Trường hợp Góc - Góc: hai tam giác có hai cặp góc bằng nhau là hai tam giác đồng dạng với nhau
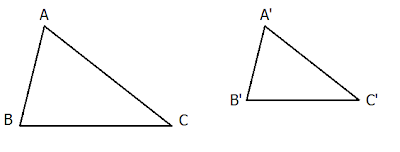
Ở hình dưới đây, nếu chúng ta chỉ ra được∠A=∠A′ và ∠B=∠B′thì chúng ta có thể kết luận rằng hai tam giác ABC và A′B′C′ là đồng dạng với nhau.

Trường hợp Cạnh - Cạnh - Cạnh: hai tam giác có ba cặp cạnh tỉ lệ với nhau là hai tam giác đồng dạng với nhau
Ở hình dưới đây, nếu chúng ta chỉ ra đượcABA′B′=BCB′C′=CAC′A′
thì chúng ta có thể kết luận rằng hai tam giác ABC và A′B′C′ là đồng dạng với nhau.

Trường hợp Cạnh - Góc - Cạnh: hai tam giác có hai cặp cạnh tỉ lệ với nhau và cặp góc xen giữa hai cặp cạnh này bằng nhau thì đó là hai tam giác đồng dạng với nhau
Ở hình dưới đây, nếu chúng ta chỉ ra đượcABA′B′= BCB′C′ và ∠B=∠B′thì chúng ta có thể kết luận rằng hai tam giác ABC và A′B′C′ là đồng dạng với nhau.

- Nếu hai tam giác là hai tam giác vuông thì việc chứng minh hai tam giác là đồng dạng còn đơn giản hơn nữa. Chúng ta có các cách sau đây.
Trường hợp Góc Nhọn: hai tam giác vuông có một cặp góc nhọn bằng nhau là hai tam giác đồng dạng với nhau
Ở hình dưới đây, nếu chúng ta chỉ ra được∠A=∠A′thì chúng ta có thể kết luận rằng hai tam giác vuông ABC và A′B′C′ là đồng dạng với nhau.

Trường hợp Cạnh - Cạnh: hai tam giác vuông có hai cặp cạnh tỉ lệ với nhau là hai tam giác đồng dạng với nhau
Ở hình trên đây, nếu chúng ta chỉ ra đượcABA′B′= BCB′C′, hoặc BCB′C′= CAC′A′, hoặc CAC′A′= ABA′B′thì chúng ta có thể kết luận rằng hai tam giác vuông ABC và A′B′C′ là đồng dạng với nhau.
Đúng 0
Bình luận (0)
Hai tam giác đồng dạng vs nhau chưa chắc đã bằng nhau
Các trường hợp đồng dạng của tam giác
- TH1 : c. c. c
- TH2 : g.g
- TH3 : c.g.c
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
hai tam giác bằng nhau thì có đồng dạng với nhau hay ko ?
Theo mik thì có !!!
P/S : Ko chắc đâu , đừng ném đá nhé !!!
Đúng 0
Bình luận (0)
Mik đã bảo là mik ko chắc đâu mà sao có bạn vẫn k sai thế !!!
Đúng 0
Bình luận (0)
Hai tam giác đồng dạng chưa chắc đã bằng nhau
Đúng 0
Bình luận (0)
1. 2 tam giác đều thì đồng dạng đúng hay sai 2. 2 tam vuông thì đồng dạng đúng hay sai 3. Hai tam giác đồng dạng thì bằng nhau đúng hay sai 4. Hai tam giác vuông có cạnh huyền bằng nhau thì chúng đồng dạng đúng hay sai
1. 2 tam giác đều thì đồng dạng
2. 2 tam vuông thì đồng dạng
Hai ý đầu chưa rõ
3. Hai tam giác đồng dạng thì bằng nhau => Sai
4. Hai tam giác vuông có cạnh huyền bằng nhau thì chúng đồng dạng => Sai
Đúng 1
Bình luận (0)
TỨ giác ABCD có hai góc vuông tại đỉnh A và C, hai đường chéo AC và BD cắt nhau tại O, góc BOA bằng góc BDC. Chứng minh:
a) tam giác ABO đồng dạng tam giác DCO
b) tam giác BCO đồng dạng tam giác ADO
cho tam giác abc đồng dạng với tam giác a'b'c' gọi ah ad am lần lượt là đường cao phân giác trung tuyến xuất phát từ dỉnh a của tam giác abc ah' ad' am' lần lượt là đường cao phân giác trung tuyến xuất phát từ dỉnh a của tam giác a'b'c' chứng minh ràng tam giác abh đồng dạng vớ tam giác a'b'h'