Cho tam giác nhọn ABC có AH là đường cao. Tia phân giác của góc B cắt AC tại M. Từ M kẻ đường thẳng vuông góc với AH cắt AB tại N a) Chứng minh tứ giác BCMN là hình thang b) Chứng minh BN = MN
giúp em với ạ

Những câu hỏi liên quan
Cho tam giác nhọn \(ABC\) có \(AH\) là đường cao. Tia phân giác của góc \(B\) cắt \(AC\) tại \(M\). Từ \(M\) kẻ đường thẳng vuông góc với \(AH\) và cắt \(AB\) tại \(N\). Chứng minh rằng:
a) Tứ giác \(BCMN\) là hình thang
b) \(BN = MN\)
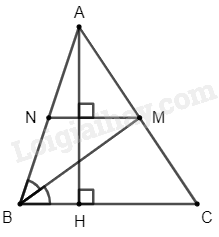
a) Ta có:
\(NM \bot AH\) (gt)
\(BC \bot AH\) (gt)
Suy ra \(NM\) // \(BC\)
Suy ra \(BNMC\) là hình thang
b) Vì \(NM\) // \(BC\) (cmt)
Suy ra \(\widehat {{\rm{NMB}}} = \widehat {{\rm{MBC}}}\) (so le trong)
Mà \(\widehat {{\rm{MBN}}} = \widehat {{\rm{MBC}}}\) (do \(MB\) là phân giác)
Suy ra \(\widehat {{\rm{MBN}}} = \widehat {{\rm{NMB}}}\)
Suy ra \(\Delta MNB\) cân tại \(N\)
Suy ra \(BN = NM\)
Đúng 0
Bình luận (0)
Cho tam giác ABC nhọn có AH vuông với BC .Vẽ tia phân giác của B cắt AC tại M. Từ M kẻ đường thẳng vuông góc với AH cắt AB tại N.
a.C/m BCMN là hình thang.
b. C/m BN =MN
a) Gọi giao điểm của NM và AH là F. Khi đó theo đề bài ta có:^MFA = ^CHF (=90o). Mà hai góc này ở vị trí đồng vị nên MN // BC.
Do đó BCMN là hình thang.
b)Đề có sai không? Nếu vẽ hình ra AB < AC thì thấy MN > BN
P/s: Không chắc ở câu a
Đúng 0
Bình luận (0)
Cho tam giác ABC nhọn(AB<AC) nội tiếp đường tròn nội tiếp đường tròntâm OĐỀ SỐ 2Kẻ đường cao AH. Gọi M, N là hình chiếu vuông góc của H lên AB, AC. Kẻ NEvuông góc với AH. Đường thẳng vuông góc với AC kẻ từ C cắt đường tròn tại I vàcắt tia AH tại D. Tia AH cắt đường tròn tại Fa) Chứng minh ABC+ACBAIC và tứ giác DENC nội tiếp.b) Chứng minh AM. AB AN . AC.c) Chứng minh tứ giác BFIC là hình thang cân.d) Chứng minh tứ giác BMED nội tiếp .
Đọc tiếp
Cho tam giác ABC nhọn(AB<AC) nội tiếp đường tròn nội tiếp đường tròn
tâm O
ĐỀ SỐ 2
Kẻ đường cao AH. Gọi M, N là hình chiếu vuông góc của H lên AB, AC. Kẻ NE
vuông góc với AH. Đường thẳng vuông góc với AC kẻ từ C cắt đường tròn tại I và
cắt tia AH tại D. Tia AH cắt đường tròn tại F
a) Chứng minh ABC+ACB=AIC và tứ giác DENC nội tiếp.
b) Chứng minh AM. AB = AN . AC.
c) Chứng minh tứ giác BFIC là hình thang cân.
d) Chứng minh tứ giác BMED nội tiếp .
Cho tam giác ABC vuông tại A (AB AC), có AH là đường cao . Kẻ HE
vuông góc AB tại E, kẻ HF vuông góc AC tại Ƒ
A) Chứng minh tứ giác AEHF là hình chữ nhật
b) lấy điểm M kẻ đường thẳng song song AH , đường thẳng này cắt tia HF tại N . Chứng minh
tứ giấc EFMH là hình bình hành
c) một mảnh đất hình chữ nhật có chiều dài là (2x+3)² mét vuông và chiều rộng là
(2x-1)² . Biết chiều dài hơn chiều rộng là 36 mét . Tính chu vi mảnh đất
Đọc tiếp
Cho tam giác ABC vuông tại A (AB < AC), có AH là đường cao . Kẻ HE
vuông góc AB tại E, kẻ HF vuông góc AC tại Ƒ
A) Chứng minh tứ giác AEHF là hình chữ nhật
b) lấy điểm M kẻ đường thẳng song song AH , đường thẳng này cắt tia HF tại N . Chứng minh
tứ giấc EFMH là hình bình hành
c) một mảnh đất hình chữ nhật có chiều dài là (2x+3)² mét vuông và chiều rộng là
(2x-1)² . Biết chiều dài hơn chiều rộng là 36 mét . Tính chu vi mảnh đất
cho tam giác ABC nhọn,Đường thẳng d vuông góc với AB tại A.tia phân giác của góc B cắt đường cao AH tại I và cắt đường thẳng d tại D.a)chứng minh tam giác AID cân b)kẻ DK vuông góc với BC tại K.Chứng minh tam giác ADI=tam giác KDI.c)trên tia đối của tia HI lấy E sao cho HE=HI.Chứng minh tứ giác ADKE là hình thang cân
Cho tam giác ABC có ba góc nhọn và ABAC. Tam giác ABC nội tiếp đường tròn (O;R). Đường cao AH của tam giác ABC cắt đường tròn (O;R) tại điểm thứ hai là D. Kẻ DM vuông góc với AB tại M.a) Chứng minh tứ giác BDHM nội tiếp đường tròn.b) Chứng minh DA là tia phân giác của MDCc) Gọi N là hình chiếu vuông góc của D lên đường thẳng AC, chứng minh ba điểm M, H, N thẳng hàng.d) Chứng minh AB2 + AC2 + CD2 + BD2 8R2
Đọc tiếp
Cho tam giác ABC có ba góc nhọn và AB>AC. Tam giác ABC nội tiếp đường tròn (O;R). Đường cao AH của tam giác ABC cắt đường tròn (O;R) tại điểm thứ hai là D. Kẻ DM vuông góc với AB tại M.
a) Chứng minh tứ giác BDHM nội tiếp đường tròn.
b) Chứng minh DA là tia phân giác của MDC
c) Gọi N là hình chiếu vuông góc của D lên đường thẳng AC, chứng minh ba điểm M, H, N thẳng hàng.
d) Chứng minh AB2 + AC2 + CD2 + BD2 = 8R2
1. Cho tam giác AB, tia phân giác của góc B cắt AC tại D. Qua D kẻ tia Dx song song với AB, Dx cắt BC tại M. kẻ tia My là phân giác của góc DMC, Bz là tia phân giác của góc ngoài tại đỉnh B. Chứng minh: Bz vuông góc My.2. Cho tam giác ABC vuông tại A, đường cao AH, có AB 12cm, BC 15cm. a, Tính AC, AH. b, So sánh HB và HC. c, Trên đoạn thẳng HC lấy điểm M bất kỳ. Qua M kẻ đường thẳng song song với AC cắt AH tại D. Chứng minh: BD vuông góc AM
Đọc tiếp
1. Cho tam giác AB, tia phân giác của góc B cắt AC tại D. Qua D kẻ tia Dx song song với AB, Dx cắt BC tại M. kẻ tia My là phân giác của góc DMC, Bz là tia phân giác của góc ngoài tại đỉnh B. Chứng minh: Bz vuông góc My.
2. Cho tam giác ABC vuông tại A, đường cao AH, có AB = 12cm, BC = 15cm.
a, Tính AC, AH.
b, So sánh HB và HC.
c, Trên đoạn thẳng HC lấy điểm M bất kỳ. Qua M kẻ đường thẳng song song với AC cắt AH tại D. Chứng minh: BD vuông góc AM
Diễn giải:
- Khi cộng, trừ số thập phân ta tiến hành cộng hoặc trừ các phần tương ứng của các số đó.
Ví dụ 1:
Tính 0,25 + 2,5 ta làm như sau: 5 + 0 = 5 , 2 + 5 =7, 0 + 2 = 2. Vậy 0,25 + 2,5 = 2.75
Tính 8,6 - 2,7 ta làm như sau: 6 - 7 không trừ được ta lấy 16 - 7 = 9, tiếp tục 8 - 2 trừ thêm 1 nữa tức là 8 -3 = 5. Vậy 8,6 - 2,7 = 5,9
- Với phép nhân, chia các số thập phân ta cần viết chúng dưới dạng phân số.
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A (AB< AC) AH là đường cao, Tia phân giác của góc CAH cắt BC tại D Qua D kẻ DK vuông góc AC tại K . Tia phân giác của góc ABC cắt DK tại E.
a)Chứng minh tam giác BAD cân
b)Chứng minh tứ giác ABDE là hình thoi.
c)Tìm điều kiện của tam giác vuông ABC để tứ giác ABCE là hình thang cân.
Cho tam giác ABC nhọn, kẻ đường cao AH (H thuộc cạnh BC). Tia phân giác của góc ABH cắt AH tại I. Qua A kẻ đường thẳng vuông góc với AB, cắt tia BI tại K. Kẻ KD vuông góc với BC (D thuộc BC). a) Chứng minh rằng: tam giác AKD cân. b) Chứng minh rằng: BK vuông gióc với AD . Từ đó suy ra I là trực tâm của tam giác ABD. c) Trên tia đối của tia HA lấy điểm E sao cho HE HI. Chứng minh rằng AKDE là hình thang cân. d) Nếu biết rằng ADE 3ADK , tính số đo ABC.
Đọc tiếp
Cho tam giác ABC nhọn, kẻ đường cao AH (H thuộc cạnh BC). Tia phân giác của góc ABH cắt AH tại I. Qua A kẻ đường thẳng vuông góc với AB, cắt tia BI tại K. Kẻ KD vuông góc với BC (D thuộc BC). a) Chứng minh rằng: tam giác AKD cân. b) Chứng minh rằng: BK vuông gióc với AD . Từ đó suy ra I là trực tâm của tam giác ABD. c) Trên tia đối của tia HA lấy điểm E sao cho HE = HI. Chứng minh rằng AKDE là hình thang cân. d) Nếu biết rằng ADE 3ADK , tính số đo ABC.














