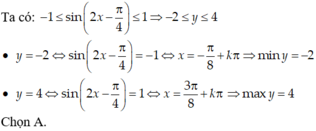D=2x²+y²+6x+2y+2xy+2017

=x²+4x+4+x²+y²+1+2x+2y+2xy+2012

=(x+2)²+(x+y+1)²+2012\(\ge\)2012

Dấu = khi x=-2 và y=1

Vậy MinA=2012 khi x=-2 và y=1

\(A=x^2+4\ge4\)

vậy giá trị nhỏ nhất của biểu thức là 4 khi x = 0 

\(x^2+4x+4=\left(x+2\right)^2\)

Vì \(x\ne-2;x>0\)

nên biểu thức có giá trị nhỏ nhất là 9 khi x = 1

b) \(x^2+4x+4=\left(x+2\right)^2\)

Vì \(\left(x+2\right)^2\ge0;\forall x\)

Dấu "=" xảy ra\(\Leftrightarrow x+2=0\)

                        \(\Leftrightarrow x=-2\)

Vậy MIN của biêu thức =0 \(\Leftrightarrow x=-2\)

Đáp án C

Ta có: y ' = 4 x 3 − 4 x = 0 ⇔ 4 x x 2 − 1 = 0 ⇔ x = 0 x = ± 1  

Mà y 0 = 3 ; y 1 = 2 ; y 2 = 11 ⇒ M = 11 , m = 2.  

\(A=\left(x-4\right)^2+1\)

Ta có: \(\left(x-4\right)^2\ge0\Rightarrow\left(x-4\right)^2+1\ge1\Rightarrow A\ge1\)

\(A_{min}=1\Leftrightarrow x=4\)

\(B=\left|3x-2\right|-5\)

Ta có: \(\left|3x-2\right|\ge0\Rightarrow\left|3x-2\right|-5\ge-5\Rightarrow B\ge-5\)

\(B_{min}=-5\Leftrightarrow x=\dfrac{2}{3}\)

\(C=5-\left(2x-1\right)^4\)

Ta có: \(\left(2x-1\right)^4\ge0\forall x\Rightarrow-\left(2x-1\right)^4\le0\forall x\Rightarrow5-\left(2x-1\right)^4\le5\Rightarrow C\le5\)

\(C_{max}=5\Leftrightarrow x=\dfrac{1}{2}\)

\(D=-3\left(x-3\right)^2-\left(y-1\right)^2-2021\)

Ta có: \(\left\{{}\begin{matrix}-3\left(x-3\right)^2\le0\forall x\\-\left(y-1\right)^2\le0\forall y\end{matrix}\right.\Rightarrow-3\left(x-3\right)^2-\left(y-1\right)^2\le0\forall x,y\Rightarrow-3\left(x-3\right)^2-\left(y-1\right)^2-2021\le-2021\Rightarrow D\le-2021\)

\(D_{max}=-2021\Leftrightarrow\left\{{}\begin{matrix}x=3\\y=1\end{matrix}\right.\)

\(E=-\left|x^2-1\right|-\left(x-1\right)^2-y^2-2020\)

\(=-\left|\left(x-1\right)\left(x+1\right)\right|-\left(x-1\right)^2-y^2-2020\)

Ta có: \(\left\{{}\begin{matrix}\left|\left(x-1\right)\left(x+1\right)\right|\ge0\forall x\Rightarrow-\left|\left(x-1\right)\left(x+1\right)\right|\le0\\\left(x-1\right)^2\ge0\forall x\Rightarrow-\left(x-1\right)^2\le0\\y^2\ge0\Rightarrow-y^2\le0\end{matrix}\right.\Rightarrow E\le-2020\)

\(E_{max}=-2020\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=0\end{matrix}\right.\)

Lời giải:

$M=\frac{x+1}{x^2+x+1}$

$\Leftrightarrow M(x^2+x+1)=x+1$
$\Leftrightarrow Mx^2+x(M-1)+(M-1)=0(*)$

Vì $M$ tồn tại PT $(*)$ luôn có nghiệm.

$\Leftrightarrow \Delta=(M-1)^2-4M(M-1)\geq 0$

$\Leftrightarrow (M-1)(M-1-4M)\geq 0$

$\Leftrightarrow (M-1)(-1-3M)\geq 0$

$\Leftrightarrow (M-1)(3M+1)\leq 0$

$\Leftrightarrow \frac{-1}{3}\leq M\leq 1$
Vậy $M_{\min}=\frac{-1}{3}; M_{\max}=1$

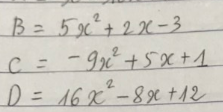
Lời giải:
$B=5x^2+2x-3=5(x^2+\frac{2}{5}x+\frac{1}{5^2})-\frac{16}{5}$

$=5(x+\frac{1}{5})^2-\frac{16}{5}$

$\geq 5.0-\frac{16}{5}=\frac{-16}{5}$
Vậy GTNN của $B$ là $\frac{-16}{5}$. Giá trị này đạt tại $x+\frac{1}{5}=0\Leftrightarrow x=-\frac{1}{5}$

---------------------------------

$C=-9x^2+5x+1=1-(9x^2-5x)$

$=\frac{61}{36}-[(3x)^2-2.3x.\frac{5}{6}+(\frac{5}{6})^2]$

$=\frac{61}{36}-(3x-\frac{5}{6})^2$

$\leq \frac{61}{36}$

Vậy gtln của $C$ là $\frac{61}{36}$. Giá trị này đạt tại $3x-\frac{5}{6}=0\Leftrightarrow x=\frac{5}{18}$

-----------------------

$D=16x^2-8x+12=(4x)^2-2.4x.1+1+11$

$=(4x-1)^2+11\geq 0+11=11$

Vậy gtnn của $D$ là $11$. Giá trị này đạt tại $4x-1=0\Leftrightarrow x=\frac{1}{4}$