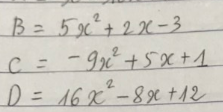Lời giải:
$B=5x^2+2x-3=5(x^2+\frac{2}{5}x+\frac{1}{5^2})-\frac{16}{5}$
$=5(x+\frac{1}{5})^2-\frac{16}{5}$
$\geq 5.0-\frac{16}{5}=\frac{-16}{5}$
Vậy GTNN của $B$ là $\frac{-16}{5}$. Giá trị này đạt tại $x+\frac{1}{5}=0\Leftrightarrow x=-\frac{1}{5}$
---------------------------------
$C=-9x^2+5x+1=1-(9x^2-5x)$
$=\frac{61}{36}-[(3x)^2-2.3x.\frac{5}{6}+(\frac{5}{6})^2]$
$=\frac{61}{36}-(3x-\frac{5}{6})^2$
$\leq \frac{61}{36}$
Vậy gtln của $C$ là $\frac{61}{36}$. Giá trị này đạt tại $3x-\frac{5}{6}=0\Leftrightarrow x=\frac{5}{18}$
-----------------------
$D=16x^2-8x+12=(4x)^2-2.4x.1+1+11$
$=(4x-1)^2+11\geq 0+11=11$
Vậy gtnn của $D$ là $11$. Giá trị này đạt tại $4x-1=0\Leftrightarrow x=\frac{1}{4}$