Cho 1 đường tròn (O),đường kính AB,lấy điểm M ϵ đường tròn (O) và tiếp tuyến tại M cắt tiếp tuyến tại A và B của đường tròn (O) ở C và D,AM cắt OC tại E, BM cắt OD tại F
a) C/m ∠COD = 90❆
b)Tứ giác MEOF là hình gì?Chứng minh
c)C/m AB là tiếp tuyến của đường tròn,đường kính CD
-GIÚP MÌNH VỚI Ạ-

Những câu hỏi liên quan
Cho nửa đường tròn tâm O đường kính AB và M là điểm nằm trên (O). Tiếp tuyến tại M cắt tiếp tuyến tại A và B của (O) lần lượt ở C và D. Đường thẳng AM cắt OC tại E, đường thẳng BM cắt OD tại Fa, Chứng minh:
C
O
D
^
90
0
b, Tứ giác MEOF là hình gì?c, Chứng minh AB là tiếp tuyến của đư...
Đọc tiếp
Cho nửa đường tròn tâm O đường kính AB và M là điểm nằm trên (O). Tiếp tuyến tại M cắt tiếp tuyến tại A và B của (O) lần lượt ở C và D. Đường thẳng AM cắt OC tại E, đường thẳng BM cắt OD tại F
a, Chứng minh: C O D ^ = 90 0
b, Tứ giác MEOF là hình gì?
c, Chứng minh AB là tiếp tuyến của đường tròn đường kính CD
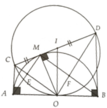
a, Dễ thấy A M B ^ = 90 0 hay E M F ^ = 90 0 tiếp tuyến CM,CA
=> OC ⊥ AM => O E M ^ = 90 0 Tương tự => O F M ^ = 90 0
Chứng minh được ∆CAO = ∆CMO => A O C ^ = M O C ^
=> OC là tia phân giác của A M O ^
Tương tự OD là tia phân giác của B O M ^ suy ra OC ⊥ OD <=> C O D ^
b, Do ∆AOM cân tại O nên OE là đường phân giác đồng thời là đường cao
=> O E M ^ = 90 0 chứng minh tương tự O F M ^ = 90 0
Vậy MEOF là hình chữ nhật
c, Gọi I là trung điểm CD thì I là tâm đường tròn đường kính CD và IO=IC=ID. Có ABDC là hình thang vuông tại A và B nên IO//AC//BD và IO vuông góc với AB. Do đó AB là tiếp tuyến của đường tròn đường kính CD.
Đúng 1
Bình luận (0)
Cho nửa đường tròn tâm O bán kính AB . Lấy M trên (O) và tiếp tuyến tại M cắt tiếp tuyến tại A và B của (O) ở C và D , AM cắt OC tại E , BM cắt OD tại F
a, Chứng minh góc COD = 90 độ
b, Tứ giác MÈO là hình j
c, Chứng minh AB là tiếp tuyến của đường tròn đường kính CD
Bài 1: Cho nữa đường tròn tâm O đường kính AB. Lấy M trên (O) và tiếp tuyến tại M cắt tiếp tuyến tại A và B của (O) ở C và D; AM cắt OC tại E, BM cắt OD tại F.a) Chứng minh COD 90b) Tứ giác MEOF là hình gì?c) Chứng minh AB là tiếp tuyến của đường tròn đường kính CDBài 2: Cho tam giác ABC có hai đường cao BD, CE cắt nhau tại H.a) Chứng minh bốn điểm A, D, H, E cùng nằm trên đường tròn (O)b) Gọi M là trung điểm của BC. Chứng minh ME là tiếp tuyến của (O).
Đọc tiếp
Bài 1: Cho nữa đường tròn tâm O đường kính AB. Lấy M trên (O) và tiếp tuyến tại M cắt tiếp tuyến tại A và B của (O) ở C và D; AM cắt OC tại E, BM cắt OD tại F.
a) Chứng minh <COD= 90
b) Tứ giác MEOF là hình gì?
c) Chứng minh AB là tiếp tuyến của đường tròn đường kính CD
Bài 2: Cho tam giác ABC có hai đường cao BD, CE cắt nhau tại H.
a) Chứng minh bốn điểm A, D, H, E cùng nằm trên đường tròn (O)
b) Gọi M là trung điểm của BC. Chứng minh ME là tiếp tuyến của (O).
Cho đường tròn (O;R) có đường kính AB. Tiếp tuyến tại M bất kì thuộc đường tròn (O) cắt các tiếp tuyến tại A và B lần lượt tại C và Da) cm: AC+ BD CD và góc COD90 độb) cm tứ giác ACMO nội tiếp và AC.BD R^2c)Tia BM cắt tia AC tại N.cm: ON vuông góc với ADd) AM cắt OC tại E, BM cắt OD tại F. Xác định vị trí điểm M để đường tròn ngoại tiếp tứ giác CEFD có bán kính nhỏ nhất.
Đọc tiếp
Cho đường tròn (O;R) có đường kính AB. Tiếp tuyến tại M bất kì thuộc đường tròn (O) cắt các tiếp tuyến tại A và B lần lượt tại C và D
a) cm: AC+ BD =CD và góc COD=90 độ
b) cm tứ giác ACMO nội tiếp và AC.BD= R^2
c)Tia BM cắt tia AC tại N.cm: ON vuông góc với AD
d) AM cắt OC tại E, BM cắt OD tại F. Xác định vị trí điểm M để đường tròn ngoại tiếp tứ giác CEFD có bán kính nhỏ nhất.
Sorry nha!!!! Mình không biết
vì mình mới học lớp 4 thôi
Đúng 0
Bình luận (0)
BÀI 1 Cho đường tròn ( O) đường kính AB , vẽ bán kính OC vuông góc với AB. Từ B vẽ tiếp tuyến Bx. Gọi M là trung điểm OC , AM kéo dài cắt đường tròn tại E và Bx tại I .Tiếp tuyến từ E cắt Bx tại D. Chứng minh tứ giác MODE nội tiếpBÀI 2: Cho đường tròn (O) đường kính AB, từ A và B vẽ Ax vuông góc với AB và By vuông góc BA ( Ax và By cùng phía so với bờ AB) .Vẽ tiếp tuyến xMy ( tiếp điểm M ) cắt Ax tại C và By tại D; OC cắt AM tại I và OD cắt BM tại K .Chứng minh tứ giác CIKD nội tiếp
Đọc tiếp
BÀI 1 Cho đường tròn ( O) đường kính AB , vẽ bán kính OC vuông góc với AB. Từ B vẽ tiếp tuyến Bx. Gọi M là trung điểm OC , AM kéo dài cắt đường tròn tại E và Bx tại I .Tiếp tuyến từ E cắt Bx tại D. Chứng minh tứ giác MODE nội tiếp
BÀI 2: Cho đường tròn (O) đường kính AB, từ A và B vẽ Ax vuông góc với AB và By vuông góc BA ( Ax và By cùng phía so với bờ AB) .Vẽ tiếp tuyến x'My' ( tiếp điểm M ) cắt Ax tại C và By tại D; OC cắt AM tại I và OD cắt BM tại K .Chứng minh tứ giác CIKD nội tiếp
Cho nửa đường tròn (o), đường kính AB. Hai tiếp tuyến Ax, By trên cùng 1 mặt phẳng bờ AB chứa nửa đường tròn (o). Tiếp tuyến tại điẻm M của nửa đường tròncắt Ax tại C và By tại D a) COD là tam giác gì? b) C/m: CDAB+BD c) AM và BM cắt OC và OD lần lượt tại E và F. Tứ giác OEMF là hình gì? d) Gọi I là giao điểm 2 đường chéo OM và EF của tứ giác OEMF. Khi M thay đổi trên nửa đường tròn (o) thì điểm I chuyển động trên đường nào? Vì sao? e) Xác định vị trí của M để tứ giác OEMF là hình vuông? Tính di...
Đọc tiếp
Cho nửa đường tròn (o), đường kính AB. Hai tiếp tuyến Ax, By trên cùng 1 mặt phẳng bờ AB chứa nửa đường tròn (o). Tiếp tuyến tại điẻm M của nửa đường tròncắt Ax tại C và By tại D a) COD là tam giác gì? b) C/m: CD=AB+BD c) AM và BM cắt OC và OD lần lượt tại E và F. Tứ giác OEMF là hình gì? d) Gọi I là giao điểm 2 đường chéo OM và EF của tứ giác OEMF. Khi M thay đổi trên nửa đường tròn (o) thì điểm I chuyển động trên đường nào? Vì sao? e) Xác định vị trí của M để tứ giác OEMF là hình vuông? Tính diện tích của hình vuông này. Cho biết AB=6cm
Cho nửa đường tròn (o), đường kính AB. Hai tiếp tuyến Ax, By trên cùng 1 mặt phẳng bờ AB chứa nửa đường tròn (o). Tiếp tuyến tại điẻm M của nửa đường tròncắt Ax tại C và By tại D
a) COD là tam giác gì?
b) C/m: CDAB+BD
c) AM và BM cắt OC và OD lần lượt tại E và F. Tứ giác OEMF là hình gì?
d) Gọi I là giao điểm 2 đường chéo OM và EF của tứ giác OEMF. Khi M thay đổi trên nửa đường tròn (o) thì điểm I chuyển động trên đường nào? Vì sao?
e) Xác định vị trí của M để tứ giác OEMF là hình vuông? Tí...
Đọc tiếp
Cho nửa đường tròn (o), đường kính AB. Hai tiếp tuyến Ax, By trên cùng 1 mặt phẳng bờ AB chứa nửa đường tròn (o). Tiếp tuyến tại điẻm M của nửa đường tròncắt Ax tại C và By tại D
a) COD là tam giác gì?
b) C/m: CD=AB+BD
c) AM và BM cắt OC và OD lần lượt tại E và F. Tứ giác OEMF là hình gì?
d) Gọi I là giao điểm 2 đường chéo OM và EF của tứ giác OEMF. Khi M thay đổi trên nửa đường tròn (o) thì điểm I chuyển động trên đường nào? Vì sao?
e) Xác định vị trí của M để tứ giác OEMF là hình vuông? Tính diện tích của hình vuông này. Cho biết AB=6cm
Cho nửa đường tròn (O;R) có đường kính AB. Tiếp tuyến tại điểm M trên nửa đường tròn lần lượt cắt 2 tiếp tuyến tại A và B ở C và D.1. C/m: AC+DBCD2. C/m: Tam giác COD vuông và AC.BDR^23. OC cắt AM tại E và OD cắt BM tại F. C/m:a) Tứ giác OEMD là hình chữ nhậtb) OE.OCOF.ODR^2c) EFperpBDd) C/m: AB là tiếp tuyến của đường tròn đường kính CDe) AD cắt BC tại N. C/m: MN//AC
Đọc tiếp
Cho nửa đường tròn (O;R) có đường kính AB. Tiếp tuyến tại điểm M trên nửa đường tròn lần lượt cắt 2 tiếp tuyến tại A và B ở C và D.
1. C/m: AC+DB=CD
2. C/m: Tam giác COD vuông và AC.BD=\(R^2\)
3. OC cắt AM tại E và OD cắt BM tại F. C/m:
a) Tứ giác OEMD là hình chữ nhật
b) OE.OC=OF.OD=\(R^2\)
c) EF\(\perp\)BD
d) C/m: AB là tiếp tuyến của đường tròn đường kính CD
e) AD cắt BC tại N. C/m: MN//AC
Cho đường tròn (O) đường kính AB, Ax và By là hai tiếp tuyến của (O) tại các tiếp điểm A, B. Lấy điểm M bất kì trên nửa đường tròn (M thuộc cùng một nửa mặt phẳng bờ AB chứa Ax, By), tiếp tuyến tại M của (O) cắt Ax, By lần lượt tại C và D.1. Chứng minh: Tứ giác AOMC nội tiếp.2. Giả sử BD R√3. Tính AM.3. Nối OC cắt AM tại E, OD cắt BM tại F, kẻ MN ⊥ AB (N ∈ AB), chứng minh đường tròn ngoại tiếp ΔNEF luôn đi qua 1 điểm cố định.4. Tìm vị trí điểm M trên nửa đường tròn để bán kính đường tròn ngoại...
Đọc tiếp
Cho đường tròn (O) đường kính AB, Ax và By là hai tiếp tuyến của (O) tại các tiếp điểm A, B. Lấy điểm M bất kì trên nửa đường tròn (M thuộc cùng một nửa mặt phẳng bờ AB chứa Ax, By), tiếp tuyến tại M của (O) cắt Ax, By lần lượt tại C và D.
1. Chứng minh: Tứ giác AOMC nội tiếp.
2. Giả sử BD = R√3. Tính AM.
3. Nối OC cắt AM tại E, OD cắt BM tại F, kẻ MN ⊥ AB (N ∈ AB), chứng minh đường tròn ngoại tiếp ΔNEF luôn đi qua 1 điểm cố định.
4. Tìm vị trí điểm M trên nửa đường tròn để bán kính đường tròn ngoại tiếp tứ giác CEFD có độ dài nhỏ nhất
Cho nửa đường tròn (O) đường kính AB,Ax và By là hai tiếp tuyến của (O) tại A và B. Lấy điểm M bất kì trên nửa đường tròn, tiếp tuyến tại M của (O) cắt Ax,By lần lượt tại C và D.1) Chứng minh các tứ giác AOMC và BOMD nội tiếp.2) Giả sử BD 3 R , tính diện tích tứ giác ABDC.3) Nối OC cắt AM tại E, OD cắt BM tại F, kẻ MN ⊥ AB tại N, chứng minh ONEF là hình thang cân.4) Tìm vị trí ‘của M trên nửa đường tròn để chu vi đường tròn ngoại tiếp tam giác CEF nhỏ nhất.
Đọc tiếp
Cho nửa đường tròn (O) đường kính AB,Ax và By là hai tiếp tuyến của (O) tại A và B. Lấy điểm M bất kì trên nửa đường tròn, tiếp tuyến tại M của (O) cắt Ax,By lần lượt tại C và D.
1) Chứng minh các tứ giác AOMC và BOMD nội tiếp.
2) Giả sử BD = 3 R , tính diện tích tứ giác ABDC.
3) Nối OC cắt AM tại E, OD cắt BM tại F, kẻ MN ⊥ AB tại N, chứng minh ONEF là hình thang cân.
4) Tìm vị trí ‘của M trên nửa đường tròn để chu vi đường tròn ngoại tiếp tam giác CEF nhỏ nhất.
Bạn tự vẽ hình nhé :
1.Vì CM,CA là tiếp tuyến của (O)
\(\Rightarrow CM\perp OM,CA\perp OA\)
\(\Rightarrow CAOM\)nội tiếp đường tròn đường kính OC
Tương tự DMOB nội tiếp đường tròn đường kính OD
2 . Vì CM,CA là tiếp tuyến của (O)
\(\Rightarrow CM=CA,OC\) là phân giác \(\widehat{AOM}\)
Tương tự DM = DB , OD là phân giác ^BOM
Mà \(\widehat{AOM}+\widehat{MOB}=180^0\)
\(\Rightarrow OC\perp OD\)
Lại có ; \(OM\perp CD\Rightarrow CM.DM=OM^2\Rightarrow CM.DM=R^2\)
Mà : \(CM=CA,DM=DB\Rightarrow AC.BD=R^2\Rightarrow AC.3R=R^2\Rightarrow AC=\frac{R}{3}\)
\(\Rightarrow S_{ABCD}=\frac{1}{2}AB\left(BD+CA\right)=\frac{1}{2}.2R.\left(3R+\frac{R}{3}\right)=\frac{10R^2}{3}\)
3.Vì CM,CA là tiếp tuyến của (O)
\(\Rightarrow CO\perp AM=E\) là trung điểm AM
Tương tự \(OD\perp BM=F\) là trung điểm BM
\(\Rightarrow MN\) là đường trung bình \(\Delta ABC\Rightarrow EF//MN\)
Mà \(OE\perp ME,OF\perp MF,MN\perp ON\)
\(\Rightarrow M,E,N,O,F\in\) đường tròn đường kính OM
\(\Rightarrow EFNO\) nội tiếp
\(\Rightarrow\widehat{EFO}+\widehat{ENO}=180^0\)
Mà \(\widehat{NEF}+\widehat{ENO}=180^0\) ( EF // AB => EF//NO )
\(\Rightarrow EFON\) là hình thang cân













