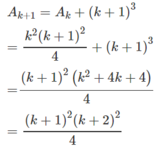m3+n3+p3-3nmp=(m+n+p)(m2+n2+p2-mn-np-mp)
chứng minh đẳng thức sau
Những câu hỏi liên quan
Chứng minh :
m3 + n3 + p3 -3mnp = (m+n+p)(m2 + n2 + p2 - mn - np - mp)
\(m^3+n^3+p^3-3mnp=\left(m^3+3m^2n+3mn^2+n^3\right)+p^3-3mnp-3m^2n-3mn^2=\left(m+n\right)^3+p^3-3mn\left(m+n+p\right)\)
\(=\left(m+n+p\right)\left[\left(m+n\right)^2-\left(m+n\right)p-p^2\right]-3mn\left(m+n+p\right)\)
\(=\left(m+n+p\right)\left(m^2+2mn+n^2-mp-np-p^2\right)-3mn\left(m+n+p\right)\)
\(=\left(m+n+p\right)\left(m^2+2mn+n^2-mp-np-p^2-3mn\right)\)
\(=\left(m+n+p\right)\left(m^2+n^2+p^2-mn-np-mp\right)\)
Đúng 1
Bình luận (0)
Chứng minh hằng đẳng thức sau:
\(m^3+n^3+p^3-3nmp=\left(m+n+p\right)\left(m^2+n^2+p^2-mn-np-mp\right)..\)
m3 + n3 + p3 - 3nmp = ( m + n + p)( m2 + n2 + p2 - mn - np - mp)
Ta có: VP= ( m + n + p)( m2 + n2 + p2 - mn - np - mp)
= m.m2 + m.n2 + m.p2 - m.mn - m.np - m.mp + n.m2 + n.n2 + n.p2 - n.mn - n.np - n.mp + p.m2 + p.n2 + p.p2 - p.mn - p.np - p.mp ( bước này k ghi củng được, mình ghi cho bạn hỉu thoii)
= m3 + mn2 + mp2 - m2n - mnp - m2p + m2n + n3 + np2 - mn2 - n2p - mnp + m2p + n2p + p3 - mnp - np2 - mp2
= m3 + n3 + p3 - 3mnp = VT (đpcm)
Đúng 0
Bình luận (0)
Bài 1 : Phân tích các đa thức sau thành nhân tửa) m3p + m2np - m2p2 - mnp2 b) ab( m2 + n2 ) + mn( a2 + b2 )Bài 2 : Phân tích các đa thức sau thành nhân tử a) (xy + ab )2 + ( ay - bx )2b) m2( n - p ) + n2( p - m ) + p2?( m - n )Bài 3 : Tìm y để giá trị của biểu thức 1 + 4y - y2 là lớn nhấtBài 4 : Tìm x , biết : ( x3 - x2 ) - 4x2 + 8x - 4 0Bài 5 : Phân tích đa thức sau thành nhân tử A ( a + b + c )3 - ( a + b - c )3 - ( b + c - a )3 - ( c + a - b )3
Đọc tiếp
Bài 1 : Phân tích các đa thức sau thành nhân tử
a) m3p + m2np - m2p2 - mnp2
b) ab( m2 + n2 ) + mn( a2 + b2 )
Bài 2 : Phân tích các đa thức sau thành nhân tử
a) (xy + ab )2 + ( ay - bx )2
b) m2( n - p ) + n2( p - m ) + p2?( m - n )
Bài 3 : Tìm y để giá trị của biểu thức 1 + 4y - y2 là lớn nhất
Bài 4 : Tìm x , biết : ( x3 - x2 ) - 4x2 + 8x - 4 = 0
Bài 5 : Phân tích đa thức sau thành nhân tử
A = ( a + b + c )3 - ( a + b - c )3 - ( b + c - a )3 - ( c + a - b )3
Bài 4:
Ta có: \(\left(x^3-x^2\right)-4x^2+8x-4=0\)
\(\Leftrightarrow x^2\left(x-1\right)-4\left(x-1\right)^2=0\)
\(\Leftrightarrow\left(x-1\right)\left(x-2\right)^2=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=2\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Câu 9. Cho tam giác MNP. Bất đẳng thức nào sau đây đúng.
A. MN + MP < NP.
B. MN +MP = NP.
C. MN – MP > NP > MN + MP.
D. MN – MP < NP < MN + MP.
Xem chi tiết
Cho hình vẽ, đuong thang m//n, m3 =63°.tính m2,m4,n1,n2,n3
Xem chi tiết
Bài 2: Tính giá trị của các biểu thức sau
a) A = 2 (m3 + n3) − 3 (m2 + n2), với m + n = 1;
b) B = 2m6 + 3m3n3 + n6 + n3, với m3 + n3 = 1;
c) C = (a − 1)3 − 4a (a + 1) (a − 1) + 3 (a − 1) (a2 + a + 1) với a = −3;
d) D = (y − 1) (y − 2) (1 + y + y2) (4 + 2y + y2) với y = 1
a: \(A=2\left(m^3+n^3\right)-3\left(m^2+n^2\right)\)
\(=2\left[\left(m+n\right)^3-3mn\left(m+n\right)\right]-3\left[\left(m+n\right)^2-2mn\right]\)
\(=2-6mn-3+6mn\)
=-1
c: \(C=\left(a-1\right)^3-4a\left(a+1\right)\left(a-1\right)+3\left(a-1\right)\left(a^2+a+1\right)\)
\(=a^3-3a^2+3a-1-4a\left(a^2-1\right)+3a^3-3\)
\(=4a^3-3a^2+3a-4-4a^3+4a\)
\(=-3a^2+7a-4\)
\(=-3\cdot9-21-4\)
=-27-21-4
=-52
Đúng 0
Bình luận (0)
Bài 2 : Phân tích các đa thức sau thành nhân tử
a) (xy + ab )2 + ( ay - bx )2
b) m2( n - p ) + n2( p - m ) + p2?( m - n )
a: \(\left(xy+ab\right)^2+\left(bx-ay\right)^2\)
\(=x^2y^2+a^2b^2+x^2b^2+a^2y^2\)
\(=x^2\left(b^2+y^2\right)+a^2\left(b^2+y^2\right)\)
\(=\left(b^2+y^2\right)\left(x^2+a^2\right)\)
Đúng 0
Bình luận (0)
Cho tam giác MNP cân tại M có MN =MP 8cm , NP=10cm.
Kẻ MI vuông góc với NP (I thuộc NP)
a chứng minh rằng: IB =IC
b. Kẻ IH vuông góc với MN (H thuộc MN),IK vuông với MP (K thuộc MP). Chứng minh IH=IK
Chứng minh các đẳng thức sau (
v
ớ
i
n
∈
N
*
)
1
3
+
2
3
+
3
3
+
.
.
.
+
n
3...
Đọc tiếp
Chứng minh các đẳng thức sau ( v ớ i n ∈ N * ) 1 3 + 2 3 + 3 3 + . . . + n 3 = n 2 n + 1 2 4
Đặt vế trái bằng A n
Dễ thấy với n = 1 hệ thức đúng.
Giả sử đã có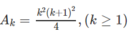 
Ta có:
Đúng 0
Bình luận (0)