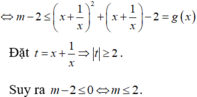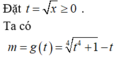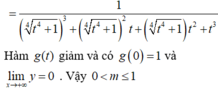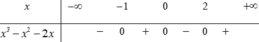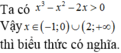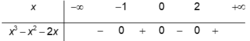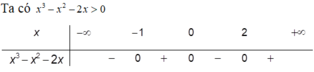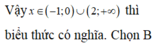Tất cả các giá trị của x để biểu thức 1x−14−x2−−−−−√ có nghĩa là

Những câu hỏi liên quan
Tất cả các giá trị của x để biểu thức 1x−14−x2−−−−−√ có nghĩa là
Tìm tất cả các giá trị thực của m để bất phương trình
x
2
-
1
x
-
1
x
3
+
x
2
-
x
2
2
-...
Đọc tiếp
Tìm tất cả các giá trị thực của m để bất phương trình x 2 - 1 x - 1 x 3 + x 2 - x 2 2 - m + x 2 - 1 x - 1 ≥ 0 , ∀ x ∈ ℝ
A. m ≤ 2
B. m ≤ - 1 4
C. m ≤ 6
D. m ≤ 1
Tất cả các giá trị của tham số m để phương trình
x
2
+
1
x
2
−
2
m
x
+
1
x
+
1
0
có nghiệm là: A.
m
∈...
Đọc tiếp
Tất cả các giá trị của tham số m để phương trình x 2 + 1 x 2 − 2 m x + 1 x + 1 = 0 có nghiệm là:
A. m ∈ 3 4 ; + ∞
B. m ∈ − ∞ ; 3 4 ∪ 3 4 ; + ∞
C. m ∈ − ∞ ; − 3 4
D. m ∈ − 3 4 ; 3 4
Ta có: x 2 + 1 x 2 − 2 m x + 1 x + 1 = 0
x + 1 x 2 − 2 m x + 1 x − 1 = 0 ( 1 )
Đặt x + 1 x = t , t ≥ 2 ta được t 2 − 2 m t − 1 = 0 ( 2 )
Phương trình (2) luôn có hai nghiệm t 1 < 0 < t 2 d o a , c = - 1 < 0 a ⇒ phương trình (1) có nghiệm khi và chỉ khi phương trình (2) có ít nhất một nghiệm t sao cho t ≥ 2 , hay ít nhất một trong hai số 2; −2 phải nằm giữa hai nghiệm t 1 , t 2 hay f ( 2 ) ≤ 0 f ( − 2 ) ≤ 0 ⇔ 3 − 4 m ≤ 0 3 + 4 m ≤ 0 ⇔ m ≥ 3 4 m ≤ − 3 4

Đáp án cần chọn là: B
Đúng 0
Bình luận (0)
Cho phương trình
x
2
– (2m + 1)x +
m
2
+ 1 0, với m là tham số. Tìm tất cả các giá trị của m
∈
ℤ
để phương trình có hai nghiệm phân biệt
x
1
;
x
2
sao cho biểu thức
P
x
1
x...
Đọc tiếp
Cho phương trình x 2 – (2m + 1)x + m 2 + 1 = 0, với m là tham số. Tìm tất cả các giá trị của m ∈ ℤ để phương trình có hai nghiệm phân biệt x 1 ; x 2 sao cho biểu thức P = x 1 x 2 x 1 + x 2 có giá trị là số nguyên
A. m = 1
B. m = 2
C. m = −2
D. m = 0
Tập tất cả các giá trị của m để phương trình
x
2
+
1
4
-
x
m
có nghiệm là A.
(
-
∞
;
0
]
B.
(
1
;
+...
Đọc tiếp
Tập tất cả các giá trị của m để phương trình x 2 + 1 4 - x = m có nghiệm là
A. ( - ∞ ; 0 ]
B. ( 1 ; + ∞ )
C. ( 0 ; 1 ]
D. ( 0 ; 1 )
Tập hợp các giá trị của x để biểu thức
l
o
g
5
(
x
3
–
x
2
-
2
x
)
có nghĩa là
Đọc tiếp
Tập hợp các giá trị của x để biểu thức l o g 5 ( x 3 – x 2 - 2 x ) có nghĩa là
![]()
![]()
![]()
Tập hợp các giá trị của x để biểu thức
log
5
(
x
3
-
x
2
-
2
x
)
có nghĩa là
A
.
(
0
;
1
)
B
.
(
-
1
;
0
)
∪
(...
Đọc tiếp
Tập hợp các giá trị của x để biểu thức log 5 ( x 3 - x 2 - 2 x ) có nghĩa là
A . ( 0 ; 1 )
B . ( - 1 ; 0 ) ∪ ( 2 ; + ∞ )
C . ( 1 ; + ∞ )
D . ( - ∞ ; - 1 )
Tập hợp các giá trị của x để biểu thức
y
log
5
(
x
3
-
x
2
-
2
x
)
có nghĩa là A. (0; 1) B.
(
-
1
;
0
)
∪
(
2
;
+
∞
)
C. ...
Đọc tiếp
Tập hợp các giá trị của x để biểu thức y = log 5 ( x 3 - x 2 - 2 x ) có nghĩa là
A. (0; 1)
B. ( - 1 ; 0 ) ∪ ( 2 ; + ∞ )
C. ( 1 ; + ∞ )
D. ( - ∞ ; - 1 )
Tìm tất cả các giá trị thực của tham số
m
để hàm số
y
x
3
+
x
2
−
2
m
+
1
x
+
4
có đúng hai cực trị . A.
m
−
2
3
B.
m
−...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để hàm số y = x 3 + x 2 − 2 m + 1 x + 4 có đúng hai cực trị .
A. m > − 2 3
B. m > − 4 3
C. m < − 2 3
D. m < 4 3
Đáp án là A
Ta có y ' = 3 x 2 + 2 x − 2 m + 1
Hàm số có đúng hai cực trị ⇔ y ' = 0 có hai nghiệm phân biệt
Tức là Δ ' = 1 + 3 2 m + 1 > 0 ⇔ m > − 2 3 .
Đúng 0
Bình luận (0)