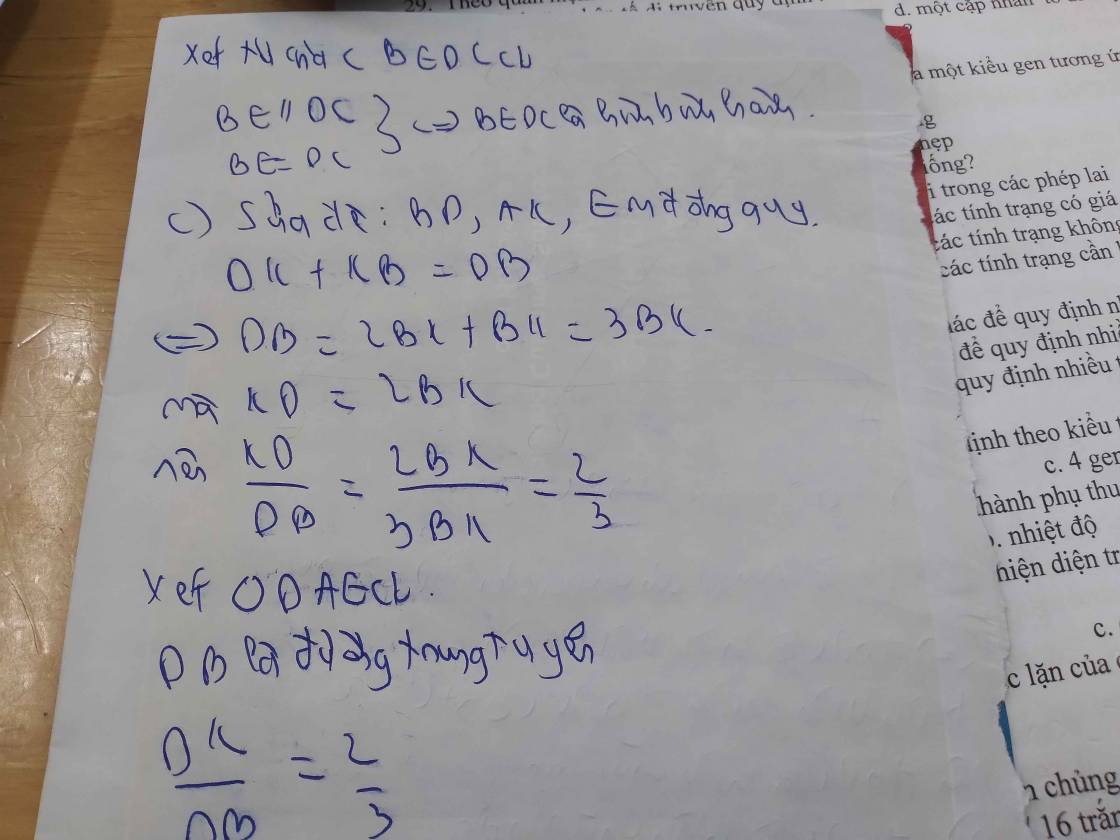cho tam giác ABC, góc BAC bằng 90 độ, có AM là đường trung tuyến, trên tia đối của MA, lấy D sao cho MA bằng MD. Chứng minh ABDC là hình chữ nhật,, cho BC bằng 8cm, tính MC. chứng minh NEDF là hình bình hành, tính hóc AEF

Những câu hỏi liên quan
cho tam giác ABC vuông tại A, có AM là đường trung tuyến . Trên tia đối của tia MA lấy D sao cho MD = MA
1) chứng minh tứ giác ABDC là hình chữ nhật . Nếu cho BC = 8cm . Hãy tính MD
2) kẻ AH vuông góc BC tại H . Gọi N,E,F lần lượt là trung điểm của AH,BH,DC
a) chứng minh tứ giác NEDF là hình bình hành
b) Tính góc AEF
Cho tam giác ABC cân tại A có AM là đường trung tuyến
a) chứng minh tam giác AMB bằng tam giác AMC
b)trên tia đối của MA lấy điểm D sao cho MA=MD chứng mình BC là tia phân giác của góc ABD
c)lấy điểm E trên đoạn MC sao cho EC =2EM gọi I là trung điểm của DC chứng mình 2EI < AB+CE
Cho tam giác ABC có góc A =90*,AM là trung tuyến ,trên tia đối của tia MA lấy D sao cho MA=MD
1, CMR: ABDC là hình chữ nhật
2, Kẻ AH vuông góc với BC tại H.Gọi N,E,F lần lượt là trung điểm của AH,BH,DC.
a,CMR NEDF là hình bình hành
b,Tính góc AEF
1, Xét tứ giác ABDC có :
M là trung điểm AD
Vì : DM=MA
Và M là trung điểm BC
Vì : BM=MC
=> AD và BC cắt nhau tại trung điểm mỗi đường
Hay ABCD là HBH
Mà HBH có 1 góc vuông là hình chữ nhật
Vậy đpcm
2a, Xét tam giác BHA có
BE=EH
Và AN=NH
=> EN là đtb của tam giác BHA
=> EN=1/2BA
Và EN//AB
Mà : BA//DC (Vì ABCD là HCN)
Nên : EN//DF (1)
Ta lại có : DF=1/2DC ( DF=FC)
Mà : AB=DC ( Vì ABCD là HCN)
Nên : DF=1/2AB
Mà : EN=1/2AB
=> DF=EN (2)
Từ (1)(2) suy ra : EDNF là hình bình hành
2b, mình không biết làm
Nhớ k mình nha !
Đúng 0
Bình luận (0)
1. Ta có: M là trung điểm của BC, M là trung điểm của AD => ABDC là hình bình hành
Xét tam giác ABC vuông tại A có AM là trung tuyến => AM=1/2 BC mà AM=MD => MD = 1/2 BC => tam giác BDC vuông tại D
Xét hình bình hành ABDC có góc D= 90* => ABDC là hình chữ nhật
Đúng 0
Bình luận (0)
1) Cho tam giác ABC vuông tại A, đường trung tuyến AM. Trên tia đối của tia MA lấy điểm D sao cho MD=MA.
a)Tính số đo góc ABD?
b)Chứng minh : Tam giác ABC = Tam giác BAD.
c) So sánh AM và BC.
2) Cho tam giác ABC có đường trung tuyến AM bằng nửa cạnh BC. CMR: góc BAC = 90 độ.
Cho tam giác ABC vuông tại A, AB<AC, AM là trung tuyến, AH là đường cao. Trên tia đối của MA lấy D sao cho MD = MA
Chứng minh: ABDC là hình chữ nhạtGọi I đối xứng với A qua BC. Ch/m BC//IDBIDC là hình gì? Chứng minh?E là trung điểm HC, F là trung điểm DB. Chứng minh AE vuông góc EFa, có MD=MA
BM=CM( M là trung điểm)
mà \(MA=\frac{BC}{2}\)(đường trung tuyến ứng với cạnh huyền của tam giác ABC
=> MA=MB=MD=MC hay MA+MD=MC+MD=> AD=BC
=> ABCD là hcn ( tính chất 2 đường chéo bằng nhau
Đúng 0
Bình luận (0)
xét tam giác AID có
H là tr điểm của AI(I đối xứng với A qua H)
M là trung điểm của AD
=> HM là đường trung bình của tam giác AID
=> HM song song với ID hay ID song song với BC
Đúng 0
Bình luận (0)
Cho tam giá ABC, góc BAC bằng 90 độ. M là trung điểm của BC
a) biết góc ABC bằng 2 góc ACB; góc ABC
b) trên tia đối của tia MA lấy điểm D sao cho DM bằng MA. Chứng minh tam giác ACM bằng tam giác DBM
c) chứng minh BD vuông góc với AB
a, Ta có \(\widehat{ABC}+\widehat{ACB}=90^0\Rightarrow3\widehat{ACB}=90^0\Rightarrow\left\{{}\begin{matrix}\widehat{ACB}=30^0\\\widehat{ABC}=60^0\end{matrix}\right.\)
b, Vì \(\left\{{}\begin{matrix}BM=MC\\AM=MD\\\widehat{AMC}=\widehat{BMD}\left(đối.đỉnh\right)\end{matrix}\right.\) nên \(\Delta ACM=\Delta DBM\left(c.g.c\right)\)
c, Vì \(\left\{{}\begin{matrix}AC=BD\left(\Delta ACM=\Delta DBM\right)\\AB.chung\\BC=AD\left(=2AM\right)\end{matrix}\right.\) nên \(\Delta ABC=\Delta BAD\left(c.c.c\right)\)
Do đó \(\widehat{BAC}=\widehat{ABD}=90^0\)
Vậy ...
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông tại A(AB>AC). Gọi M là trung điểm của BC. Trên tia đối của tia MA lấy điểm D sao cho MD=MA. a) Chứng minh tứ giác ABDC là hình chữ nhật. b) Gọi E là điểm đối xứng của C qua A. Chứng minh tứ giác ADBE là hình bình hành.
a) Xét ∆CMA và ∆BMD:
Góc CMA= góc BMD (đối đỉnh)
MA=MD (gt)
MC=MB (M là trung điểm BC)
=> ∆CMA=∆BMD(c.g.c)
=> góc CAM = góc BDM và CA=DB
Mà 2 góc CAM và góc BDM nằm ở vị trí so lo trong nên CA//DB
=> CABD là hình bình hành
Lại có góc CAB = 90 độ (gt)
=> ACDB là hình chữ nhật
b) Vì E là điểm đối xứng của C qua A nên EAB=90độ=DBA
Mà 2 góc này ở bị trí so le trong nên AE//DB
Lại có AE=BD(=CA)
=> AEBD là hình bình hành
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông tại A (AB < AC). Gọi M là trung điểm của BC. Trên tia đối của tia MA lấy điểm D sao cho MD = MA.
a) Chứng minh tứ giác ABDC là hình chữ nhật.
b)Lấy điểm E sao cho B là trung điểm của AE. Chứng minh tứ giác BEDC là hình bình hành. c) Lấy điểm K thuộc đoạn thẳng BD sao cho KD = 2BK. CM: EK, AC, BD là đồng quy
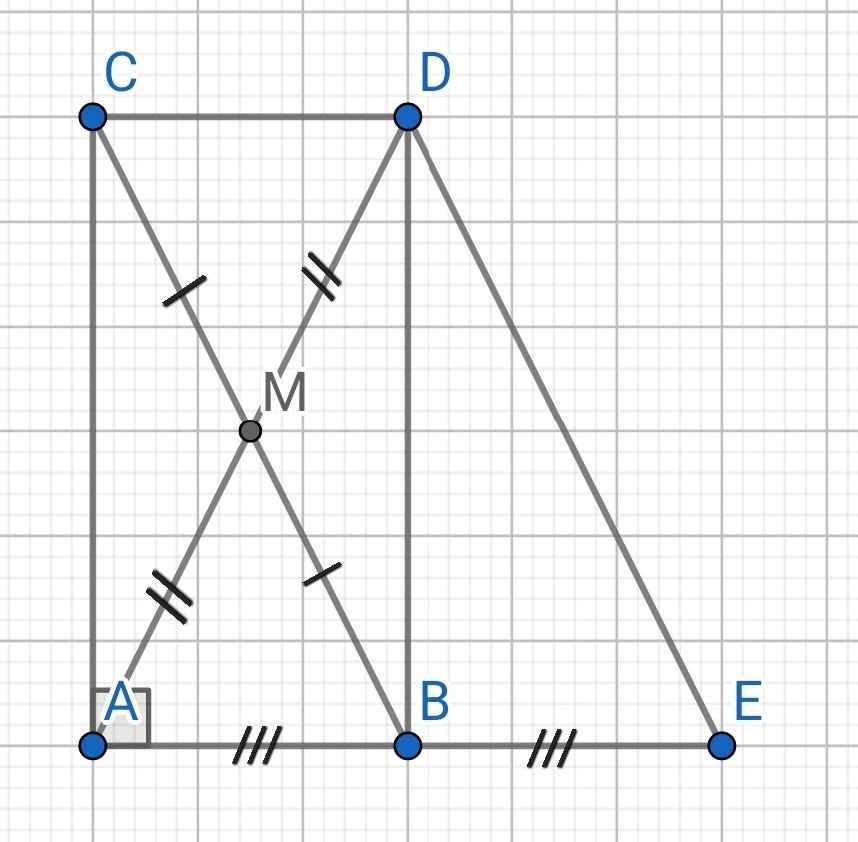 a) Tứ giác ABDC có:
a) Tứ giác ABDC có:
M là trung điểm của BC (gt)
M là trung điểm của AD (gt)
⇒ ABDC là hình bình hành
Mà ∠BAC = 90⁰ (∆ABC vuông tại A)
⇒ ABDC là hình chữ nhật
b) Do ABDC là hình chữ nhật (cmt)
⇒ CD = AB (1)
Do B là trung điểm của AE (gt)
⇒ BE = AB = AE : 2 (2)
Từ (1) và (2) ⇒ CD = BE
Do ABDC là hình chữ nhật (cmt)
⇒ CD // AB
⇒ CD // BE
Tứ giác BEDC có:
CD // BE (cmt)
CD = BE (cmt)
⇒ BEDC là hình bình hành
c) Do ABDC là hình chữ nhật (cmt)
⇒ AC // BD
Do đó AC, BD, EK đồng quy là vô lý
Em xem lại đề nhé!
Đúng 0
Bình luận (0)
Cho tam giác ABC có B bằng 90 độ vẽ trung tuyến AM Trên tia đối của tia MA lấy điểm I sao cho MI = MA a) chứng minh tam giác AMB= tam giác ICM b) cho góc BAC= 60 độ . Tính số đo gốc ACI