3. Trong các cặp tam giác dưới đây (h.91), có những cặp tam giác nào bằng nhau? Vì sao?
4. Trên hình 92 có các cặp tam giác vuông nào bằng nhau? Vì sao?
Sách Vnen
Mỗi hình sau có các cặp tam giác vuông nào bằng nhau? Vì sao?
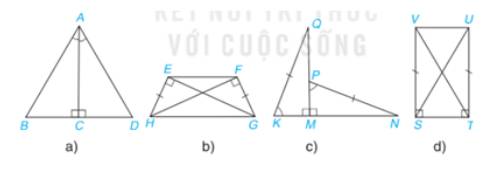
a) Xét 2 tam giác vuông ABC và ADC có:
\(\widehat {ACB} = \widehat {ACD}( = 90^\circ )\)
AC chung
\(\widehat {BAC} = \widehat {DAC}\)(gt)
=>\(\Delta ABC = \Delta ADC\)(g.c.g)
b) Xét 2 tam giác vuông HEG và GFH có:
HE=GF(gt)
HG chung
=>\(\Delta HEG = \Delta GFH\)(cạnh huyền - cạnh góc vuông)
c) Xét 2 tam giác vuông QMK và NMP có:
QK=NP(gt)
\(\widehat K = \widehat P\)(gt)
=>\(\Delta QMK = \Delta NMP\)(cạnh huyền – góc nhọn)
d) Xét 2 tam giác vuông VST và UTS có:
VS=UT(gt)
ST chung
=>\(\Delta VST = \Delta UTS\)(2 cạnh góc vuông)
Trong các tam giác dưới đây có những tam giác nào bằng nhau? Vì sao?
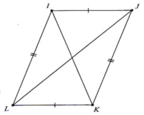
Trong Hình 4.48, hãy tìm các cặp tam giác vuông bằng nhau và giải thích vì sao chúng bằng nhau.
+)Xét hai tam giác vuông ABC và XYZ có:
\(\widehat A = \widehat X( = 90^\circ )\) (gt)
AC=XZ (gt)
\(\widehat C = \widehat Z\) (gt)
\( \Rightarrow \Delta ABC = \Delta XYZ\) (g.c.g)
+)Xét hai tam giác vuông DEF và GHK có:
\(EF = HK\) (gt)
\(\widehat {EFD} = \widehat {GKH}\) (gt)
\( \Rightarrow \Delta DEF = \Delta GHK\) (cạnh huyền – góc nhọn)
+)Xét hai tam giác vuông MNP và RTS có:
\(MN = TR\) (gt)
\(\widehat R = \widehat M( = 90^\circ )\) (gt)
\(PM = SR\) (gt)
\( \Rightarrow \Delta MNP = \Delta RTS\) (c.g.c)
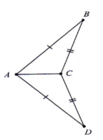
Cho tam giác ABC, trên tia đối của tia AB xác định điểm B' sao cho AB' = AB; trên tia đối của tia AC xác định điểm C' sao cho AC' = AC.
a) Hai tam giác ABC và AB'C' có bằng nhau ko ? vì sao ?
b) Hai tam giác ABC , AB'C' còn có những cặp góc, cặp cạnh nào bằng nhau nữa ?
Hình dễ bạn tự vẽ nhé !
a) Xét tam giác ABC và tam giác AB'C' có:
AC = AC'
BAC= B'AC'
AB = AB
nên tam giác ABC = tam giác AB'C' ( c.g.c )
b) Từ tam giác ABC = tam giác AB'C' => C'B' = CB, ABC = AB'C', ACB = AC'B'
Hình dễ bn tự vẽ nhé
a,Xét \(\Delta ABC\)và\(\Delta AB’C’\),có:
\(AB=AB’\)(gt)
\(AC=AC’\)(gt)
\(\widehat{BAC}=\widehat{B’AC’}\)(đối đỉnh)
\(\Rightarrow\Delta ABC=\Delta AB’C’\)(c.g.c)
b,tam giác ABC và tam giác AB’C’ có những cặp cạnh, cặp góc bằng nhau là:
BC=B’C’(2 cạnh tương ứng)
\(\widehat{ABC}=\widehat{AB’C’}\)(2 góc tương ứng)
\(\widehat{BCA}=\widehat{B’C’A}\)(2 góc tương ứng)
k mik nhé!!!
#sadgirl#
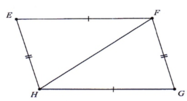
Gọi Ot là tia phân giác của xOy. Gọi A là điểm trên tia Ox và B là điểm trên tia Oy sao cho OA = OB ; gọi C là điểm trên tia Ot :
a) Hai tam giác COA ; COB có bằng nhau ko ? Vì sao ?
b) Hai tam giác COA ; COB còn có những cặp cạnh, cặp góc nào bằng nhau nữa ?
a ) Hình dễ tự vẽ
Do Ot là tia p/g của \(\widehat{xOy}\Rightarrow\widehat{tOx}=\widehat{tOy}\)
Xét hai tam giác : tam giác COA và tam giác COB có :
OA=OB ( gt)
\(\widehat{tOx}=\widehat{tOy}\)( cm trên )
OC là cạnh chung
nên tam giác COA = tam giác COB ( c.g.c )
b ) Có tam giác COA = tam giác COB
\(\Rightarrow\widehat{OCB}=\widehat{OCA}\) ; \(\widehat{CBO}=\widehat{CAO}\) ; \(\widehat{COA}=\widehat{COB}\)
\(\Rightarrow CB=CA\) ; \(OA=OB\)
Hai tam giác vuông ABC (vuông tại đỉnh A) và A’B’C’ (vuông tại đỉnh A’) có các cặp cạnh góc vuông bằng nhau: AB = A'B', AC = A'C' (H.4.45). Dựa vào trường hợp bằng nhau cạnh - góc - cạnh của hai tam giác, hãy giải thích vì sao hai tam giác vuông ABC và ABC bằng nhau.
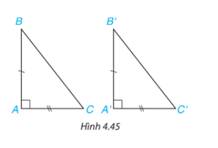
Xét 2 tam giác ABC và A’B’C có:
AB=A’B’ (gt)
\(\widehat A = \widehat {A'}\) (gt)
AC=A’C’ (gt)
\( \Rightarrow \Delta ABC = \Delta A'B'C'\)(c.g.c)
cho tam giác ABC trên tia đối của tia AB xác định điểm B' sao cho AB'=AB, trên tia đối của tia AC xác định điểm C' sao cho AC'=AC
a) hai tam giác ABC , ABC' có bằng nhau ko ? vì sao ?
b) hai tam giác ABC , AB'C' còn có những cặp góc , cặp cạnh nào bằng nhau ko ?
mình cần gấp , giải dùm mình với nhé
a, 2 tam giác ABC và tam giác AB'C' bằng nhau theo TH (c.g.c)
b, cặp góc: góc BAC và B'AC' ; góc B và B' ; góc C và C'
Cặp cạnh : AB=AB' ;AC =AC' ; BC = B'C'
chúc bạn học tốt !!! :)) :))
Trong các tam giác dưới đây, những cặp tam giác nào đồng dạng với nhau ? Hãy giải thích (h.41)
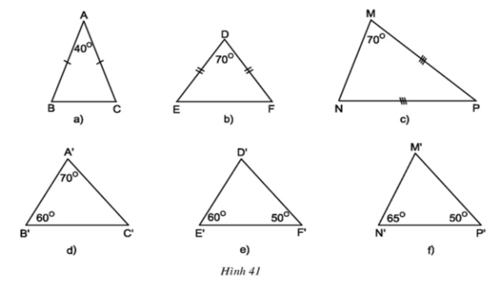
- ΔABC có ∠A + ∠B + ∠C = 180o ⇒ ∠B + ∠C = 180o - ∠A
Mà ΔABC cân tại A ⇒ ∠B = ∠C
⇒∠B = ∠C = ( 180o- 40o)/2 = 70o
ΔMNP cân tại P ⇒ ∠M = ∠N = 70o
ΔABC và ΔPMN có
∠B = ∠M = 70o)
∠C = ∠N = 70o)
⇒ ΔABC ∼ ΔPMN (g.g)
- ΔA’B’C’ có ∠A' + ∠B' + ∠C' = 180o
⇒∠C' = 180o- ( ∠A' + ∠B') = 180o - ( 70o+ 60o ) = 50o
ΔA’B’C’ và ΔD’E’F’ có
∠B' = ∠E' (= 60o)
∠C' = ∠F' (= 50o)
⇒ ΔA’B’C’ ∼ ΔD’E’F’ (g.g)
Trong các tam giác dưới đây, những cặp tam giác nào đồng dạng với nhau ? Hãy giải thích (h.41)
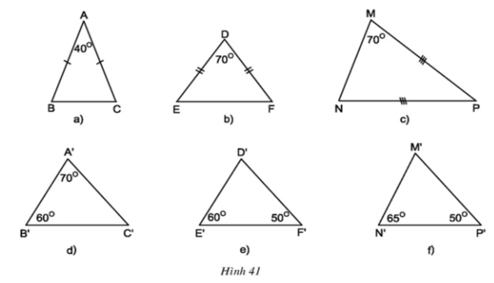
- ΔABC có ∠A + ∠B + ∠C = 180o ⇒ ∠B + ∠C = 180o - ∠A
Mà ΔABC cân tại A ⇒ ∠B = ∠C
⇒∠B = ∠C = ( 180o- 40o)/2 = 70o
ΔMNP cân tại P ⇒ ∠M = ∠N = 70o
ΔABC và ΔPMN có
∠B = ∠M = 70o)
∠C = ∠N = 70o)
⇒ ΔABC ∼ ΔPMN (g.g)
- ΔA’B’C’ có ∠A' + ∠B' + ∠C' = 180o
⇒∠C' = 180o- ( ∠A' + ∠B') = 180o - ( 70o+ 60o ) = 50o
ΔA’B’C’ và ΔD’E’F’ có
∠B' = ∠E' (= 60o)
∠C' = ∠F' (= 50o)
⇒ ΔA’B’C’ ∼ ΔD’E’F’ (g.g)