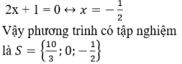\(a)x^2-9x+20=0 \\<=>(x-4)(x-5)=0 \\<=>x=4\ hoặc\ x=5 \\b)x^2-3x-18=0 \\<=>(x+3)(x-6)=0 \\<=>x=-3\ hoặc\ x=6 \\c)2x^2-9x+9=0 \\<=>(x-3)(2x-3)=0 \\<=>x=3\ hoặc\ x=\dfrac{3}{2}\)

d: \(\Leftrightarrow3x^2-6x-2x+4=0\)

=>(x-2)(3x-2)=0

=>x=2 hoặc x=2/3

e: \(\Leftrightarrow3x\left(x^2-2x-3\right)=0\)

=>x(x-3)(x+1)=0

hay \(x\in\left\{0;3;-1\right\}\)

f: \(\Leftrightarrow x^2-5x-2+x=0\)

\(\Leftrightarrow x^2-4x-2=0\)

\(\Leftrightarrow\left(x-2\right)^2=6\)

hay \(x\in\left\{\sqrt{6}+2;-\sqrt{6}+2\right\}\)

a) \(x^3-x^2+3x-3>0\)

\(\Leftrightarrow x^2\left(x-1\right)+3\left(x-1\right)>0\)

\(\Leftrightarrow\left(x^2+3\right)\left(x-1\right)>0\) 

Mà: \(x^2+3>0\forall x\) 

\(\Leftrightarrow x-1>0\)

\(\Leftrightarrow x>1\)

b) \(x^3+x^2+9x+9< 0\)

\(\Leftrightarrow x^2\left(x+1\right)+9\left(x+1\right)< 0\)

\(\Leftrightarrow\left(x^2+9\right)\left(x+1\right)< 0\)

Mà: \(x^2+9>0\forall x\)

\(\Leftrightarrow x+1< 0\)

\(\Leftrightarrow x< -1\)

d) \(4x^3-14x^2+6x-21< 0\)

\(\Leftrightarrow2x^2\left(2x-7\right)+3\left(2x-7\right)< 0\)

\(\Leftrightarrow\left(2x^2+3\right)\left(2x-7\right)< 0\)

Mà: \(2x^2+3>0\forall x\)

\(\Leftrightarrow2x-7< 0\)

\(\Leftrightarrow2x< 7\)

\(\Leftrightarrow x< \dfrac{7}{2}\)

d) \(x^2\left(2x^2+3\right)+2x^2>-3\)

\(\Leftrightarrow2x^4+3x^2+2x^2+3>0\)

\(\Leftrightarrow2x^4+5x^2+3>0\)

\(\Leftrightarrow\left(x^2+1\right)\left(2x^2+3\right)>0\) 

Mà: 

\(x^2+1>0\forall x\)

\(2x^2+3>0\forall x\)

\(\Rightarrow x\in R\)

a: =>x^2(x-1)+3(x-1)>0

=>(x-1)(x^2+3)>0

=>x-1>0

=>x>1

b: =>x^2(x+1)+9(x+1)<0

=>(x+1)(x^2+9)<0

=>x+1<0

=>x<-1

c: 4x^3-14x^2+6x-21<0

=>2x^2(2x-7)+3(2x-7)<0

=>2x-7<0

=>x<7/2

d: =>x^2(2x^2+3)+2x^2+3>0

=>(2x^2+3)(x^2+1)>0(luôn đúng)

a.

$x^4-25x^3=0$

$\Leftrightarrow x^3(x-25)=0$

\(\Leftrightarrow \left[\begin{matrix} x^3=0\\ x-25=0\end{matrix}\right.\Leftrightarrow \left[\begin{matrix} x=0\\ x=25\end{matrix}\right.\)

b.

$(x-5)^2-(3x-2)^2=0$

$\Leftrightarrow (x-5-3x+2)(x-5+3x-2)=0$

$\Leftrightarrow (-2x-3)(4x-7)=0$
\(\Leftrightarrow \left[\begin{matrix} -2x-3=0\\ 4x-7=0\end{matrix}\right.\Leftrightarrow \left[\begin{matrix} x=\frac{-3}{2}\\ x=\frac{7}{4}\end{matrix}\right.\)

c.

$x^3-4x^2-9x+36=0$

$\Leftrightarrow x^2(x-4)-9(x-4)=0$

$\Leftrightarrow (x-4)(x^2-9)=0$

$\Leftrightarrow (x-4)(x-3)(x+3)=0$

\(\Leftrightarrow \left[\begin{matrix} x-4=0\\ x-3=0\\ x+3=0\end{matrix}\right.\Leftrightarrow \left[\begin{matrix} x=4\\ x=3\\ x=-3\end{matrix}\right.\)

d. ĐK: $x\neq 0$

$(-x^3+3x^2-4x):(\frac{-1}{2}x)=0$

$\Leftrightarrow x(-x^2+3x-4):(\frac{-1}{2}x)=0$

$\Leftrightarrow -2(-x^2+3x-4)=0$

$\Leftrightarrow x^2-3x+4=0$

$\Leftrightarrow (x-1,5)^2=-1,75< 0$ (vô lý)

Vậy pt vô nghiệm.

11: \(2x^2-12xy+18y^2\)

\(=2\left(x^2-6xy+9y^2\right)\)

\(=2\left(x-3y\right)^2\)

12: \(\left(x^2+x\right)^2+3\left(x^2+x\right)+2\)

\(=\left(x^2+x+2\right)\left(x^2+x+1\right)\)

Bài 2:

a: =>2x^2-4x+1=x^2+x+5

=>x^2-5x-4=0

=>\(x=\dfrac{5\pm\sqrt{41}}{2}\)

b: =>11x^2-14x-12=3x^2+4x-7

=>8x^2-18x-5=0

=>x=5/2 hoặc x=-1/4

Ta có

x 3   +   2 x 2   –   9 x   –   18   =   0     ⇔   ( x 3   +   2 x 2 )   –   ( 9 x   +   18 )   =   0     ⇔   x 2 ( x   +   2 )   –   9 ( x   +   2 )   =   0     ⇔   ( x   +   2 ) ( x 2   –   9 )   =   0

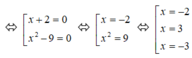
Vậy x = -2; x = 3; x =-3

Đáp án cần chọn là: D

2: \(\Leftrightarrow\left(x^2+x\right)^2-5\left(x^2+x\right)-6=0\)

\(\Leftrightarrow x^2+x-6=0\)

=>(x+3)(x-2)=0

=>x=-3 hoặc x=2

5: \(\Leftrightarrow\left(x+2\right)\left(x-1\right)\left(x+1\right)=0\)

hay \(x\in\left\{-2;1;-1\right\}\)

a)\(3x\left(x-1\right)+2x^2\left(x-1\right)=0\\ \Leftrightarrow x\left(x-1\right)\left(3+2x\right)=0\\ \Leftrightarrow\left\{{}\begin{matrix}x=0\\x-1=0\\3+2x=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\x=1\\x=\dfrac{-3}{2}\end{matrix}\right.\)

a: Ta có: \(3x^2-3x+2x^3-2x^2=0\)

\(\Leftrightarrow2x^3+x^2-3x=0\)

\(\Leftrightarrow x\left(2x^2+x-3\right)=0\)

\(\Leftrightarrow x\left(x-1\right)\left(2x+3\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=1\\x=-\dfrac{3}{2}\end{matrix}\right.\)

b: Ta có: \(x^3+27=-x^2+9\)

\(\Leftrightarrow\left(x+3\right)\left(x^2-3x+9\right)+\left(x+3\right)\left(x-3\right)=0\)

\(\Leftrightarrow\left(x+3\right)\left(x^2-3x+9+x-3\right)=0\)

\(\Leftrightarrow x+3=0\)

hay x=-3

a)  3 x 2 − 7 x − 10 ⋅ 2 x 2 + ( 1 − 5 ) x + 5 − 3 = 0

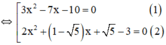
+ Giải (1):

3 x 2   –   7 x   –   10   =   0

Có a = 3; b = -7; c = -10

⇒ a – b + c = 0

⇒ (1) có hai nghiệm  x 1   =   - 1   v à   x 2   =   - c / a   =   10 / 3 .

+ Giải (2):

2 x 2   +   ( 1   -   √ 5 ) x   +   √ 5   -   3   =   0

Có a = 2; b = 1 - √5; c = √5 - 3

⇒ a + b + c = 0

⇒ (2) có hai nghiệm:

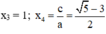
Vậy phương trình có tập nghiệm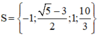 

b)

x 3 + 3 x 2 - 2 x - 6 = 0 ⇔ x 3 + 3 x 2 - ( 2 x + 6 ) = 0 ⇔ x 2 ( x + 3 ) - 2 ( x + 3 ) = 0 ⇔ x 2 - 2 ( x + 3 ) = 0

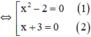
+ Giải (1): x 2   –   2   =   0   ⇔   x 2   =   2  ⇔ x = √2 hoặc x = -√2.

+ Giải (2): x + 3 = 0 ⇔ x = -3.

Vậy phương trình có tập nghiệm S = {-3; -√2; √2}

c)

x 2 − 1 ( 0 , 6 x + 1 ) = 0 , 6 x 2 + x ⇔ x 2 − 1 ( 0 , 6 x + 1 ) = x ⋅ ( 0 , 6 x + 1 ) ⇔ x 2 − 1 ( 0 , 6 x + 1 ) − x ( 0 , 6 x + 1 ) = 0 ⇔ ( 0 , 6 x + 1 ) x 2 − 1 − x = 0

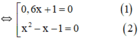
+ Giải (1): 0,6x + 1 = 0 ⇔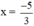 

+ Giải (2):

x 2   –   x   –   1   =   0

Có a = 1; b = -1; c = -1

⇒   Δ   =   ( - 1 ) 2   –   4 . 1 . ( - 1 )   =   5   >   0

⇒ (2) có hai nghiệm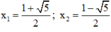 

Vậy phương trình có tập nghiệm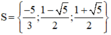 

d)

x 2 + 2 x − 5 2 = x 2 − x + 5 2 ⇔ x 2 + 2 x − 5 2 − x 2 − x + 5 2 = 0 ⇔ x 2 + 2 x − 5 − x 2 − x + 5 ⋅ x 2 + 2 x − 5 + x 2 − x + 5 = 0 ⇔ ( 3 x − 10 ) 2 x 2 + x = 0

⇔ (3x-10).x.(2x+1)=0

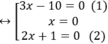
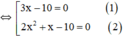
+ Giải (1): 3x – 10 = 0 ⇔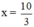 

+ Giải (2):