Cho nửa đường tròn tâm O đường kính AB. Vẽ tiếp tuyến d tiếp xúc với đường tròn tại C. Từ A và B kẻ AM và BN vuông góc với đường d. Gọi D là hình chiếu của C trên AB. Chứng minh CD^2 = AM.BN

Những câu hỏi liên quan
Cho nửa đường tròn (O) đường kính AB. Một đường thẳng d tiếp xúc với nửa đường tròn đó tịa C. Từ A và B kẻ AM vuông góc với d tại M và BN vuông góc với d tại N. Gọi N là hình chiếu của C trên AB. Chứng minh:
a. CM=CN
b. CD^2 = AM.BN
P/s: không cần vẽ hình đâu :))
BT1: Kẻ 2 tiếp tuyến AM, AN. M, N thuộc đường tròn tâm O. Từ O kẻ đường thẳng vuông góc với OM cắt AN tại S. CM: SO SA.BT2: Cho nửa đường tròn tâm O, đường kính AB. Ax là tiếp tuyến của nửa đường tròn. M thuộc Ax. Lấy Y thuộc Ax sao cho M là trung điểm của AY. BY cắt đường tròn tâm O tại C. CM: MC là tiếp tuyến của đường tròn tâm O.BT3: Cho bửa đường tròn AB, 1 đường thẳng a tiếp xúc với nửa đường tròn tại C. Tại A, B kẻ AM, BN vuông góc với đường thẳng a. Gọi D là hình chiếu của C trên AB.a) C...
Đọc tiếp
BT1: Kẻ 2 tiếp tuyến AM, AN. M, N thuộc đường tròn tâm O. Từ O kẻ đường thẳng vuông góc với OM cắt AN tại S. CM: SO = SA.
BT2: Cho nửa đường tròn tâm O, đường kính AB. Ax là tiếp tuyến của nửa đường tròn. M thuộc Ax. Lấy Y thuộc Ax sao cho M là trung điểm của AY. BY cắt đường tròn tâm O tại C. CM: MC là tiếp tuyến của đường tròn tâm O.
BT3: Cho bửa đường tròn AB, 1 đường thẳng a tiếp xúc với nửa đường tròn tại C. Tại A, B kẻ AM, BN vuông góc với đường thẳng a. Gọi D là hình chiếu của C trên AB.
a) CD2 = AM . BN
b) Góc MDN = 90 độ
Vẽ hình dùm mình luôn nha. Cảm ơn nhiều ạ <3
cho nửa đường tròn (O;R) đường kính AB. Lấy M thuộc nửa đường tròn đó sao cho AMBM. Qua M kẻ d là đường tiếp tuyến của (O). Gọi C và D là hình chiếu của A và B trên d kẻ MH vuông góc ABa) CMR A,C,M,H cùng thuộc 1 đường trònb) MB^2 BHxBA và BM là tiếp tuyến của đường tròn đg kính AMc) CMR: H thuộc đg tròn đường kính CDd) giả sử AM R và d cắt AB ở K. tiếp tuyến với (O) tại A cắt d ở E. CMR
Đọc tiếp
cho nửa đường tròn (O;R) đường kính AB. Lấy M thuộc nửa đường tròn đó sao cho AM<BM. Qua M kẻ d là đường tiếp tuyến của (O). Gọi C và D là hình chiếu của A và B trên d kẻ MH vuông góc AB
a) CMR A,C,M,H cùng thuộc 1 đường tròn
b) MB^2= BHxBA và BM là tiếp tuyến của đường tròn đg kính AM
c) CMR: H thuộc đg tròn đường kính CD
d) giả sử AM = R và d cắt AB ở K. tiếp tuyến với (O) tại A cắt d ở E. CMR
cho một đường tròn tâm (O;R) , đường kính AB. qua điểm C thuộc nửa đường tròn, kẻ tiếp tuyến d của nửa đường tròn. gọi M,N lần lượt là hình chiếu của A và B trên d. gọi H là đường vuông góc kẻ từ C đến AB.chứng minh rằng:
a) tứ giác ABNM là hình thang vuông.
b) AC là phân giác của BAM.
c) CH^2 = AM.BN
cho một đường tròn tâm (O;R) , đường kính AB. qua điểm C thuộc nửa đường tròn, kẻ tiếp tuyến d của nửa đường tròn. gọi M,N lần lượt là hình chiếu của A và B trên d. gọi H là đường vuông góc kẻ từ C đến AB.chứng minh rằng:
a) tứ giác ABNM là hình thang vuông.
b) AC là phân giác của BAM.
c) CH^2 = AM.BN
a,
Vì M,N lần lượt là hình chiếu của A và B trên d (gt) nên ta cóAM và BN cùng vuông góc với d
=> AM song song BN
Xét tứ giác AMNB có:AM song song BN(cmt)
=> AMNB là hình thang mà góc AMN = 90* ( AM vuông góc MN)
=> tg AMNB là hình thang vuông.
Vậy...
Đúng 0
Bình luận (1)
Cho nửa đường tròn tâm O có đường kính AB. Gọi M là điểm bất kì thuộc nửa đường tròn, H là chân đường vuông góc kẻ từ M đén AB. Vẽ đường tròn (M; MH). Kẻ các tiếp tuyến AC, BD với đường tròn tâm M (C và D là các tiếp điểm khác H). Chứng minh rằng ba điểm C, M, D thẳng hàng và CD là tiếp tuyến của đường tròn (O)
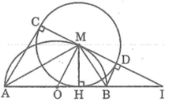
Trong đường tròn (M; MH), theo tính chất hai tiếp tuyến cắt nhau, ta có:
- MA là tia phân giác của góc HMC

Vậy C, M, D thẳng hàng.
Đúng 0
Bình luận (0)
Cho nửa đường tròn tâm O bán kính R, đường kính AB. Kẻ các tiếp tuyến Ax, By cùngphía với nửa đường tròn đối với AB. Từ điểm M trên nửa đường tròn kẻ tiếp tuyến thứ ba vớiđường tròn, tiếp tuyến này cắt Ax và By lần lượt tại C và D.a) Chứng minh: OC AM và AM // OD;b) Chứng minh: AC.BD R2c) Chứng minh: AB là tiếp tuyến đường tròn đường kính CD;d) Gọi K là giao điểm của AD và BC. Chứng minh MK AB;e) Tìm vị trí điểm M sao cho diện tích tứ giác ACDB nhỏ nhất.
Đọc tiếp
Cho nửa đường tròn tâm O bán kính R, đường kính AB. Kẻ các tiếp tuyến Ax, By cùng
phía với nửa đường tròn đối với AB. Từ điểm M trên nửa đường tròn kẻ tiếp tuyến thứ ba với
đường tròn, tiếp tuyến này cắt Ax và By lần lượt tại C và D.
a) Chứng minh: OC AM và AM // OD;
b) Chứng minh: AC.BD = R2
c) Chứng minh: AB là tiếp tuyến đường tròn đường kính CD;
d) Gọi K là giao điểm của AD và BC. Chứng minh MK AB;
e) Tìm vị trí điểm M sao cho diện tích tứ giác ACDB nhỏ nhất.
Cho nửa đường tròn tâm O đường kính AB = 2R. Trên nửa đường tròn lấy điểm C (C khác A và B). Gọi D là giao điểm của đường thẳng BC với tiếp tuyến tại A của nửa đường tròn tâm O và I là trung điểm của AD a. Chứng minh BC.BD = 4R² b. Chứng minh IC là tiếp tuyến của nửa đường tròn tâm O c. Từ C kẻ CH vuông góc với AB (H thuộc AB) BI cắt CH tại K. Chứng minh K là trung điểm của CH.
Cho nửa đường tròn tâm O, đường kính AB 2R, Ax và By là hai tiêp tuyến với nửa đường tròn tại A và B. Lấy trên tia Ax điểm M rồi vẽ tiếp tuyến MP với đường tròn tâm O (tiếp điểm P khác điểm A) cắt By tại Na, Chứng minh các tam giác MON và APB đồng dạngb, Chứng minh AM.BN
R
2
c, Tính tỉ số
S
M
O
N...
Đọc tiếp
Cho nửa đường tròn tâm O, đường kính AB = 2R, Ax và By là hai tiêp tuyến với nửa đường tròn tại A và B. Lấy trên tia Ax điểm M rồi vẽ tiếp tuyến MP với đường tròn tâm O (tiếp điểm P khác điểm A) cắt By tại N
a, Chứng minh các tam giác MON và APB đồng dạng
b, Chứng minh AM.BN = R 2
c, Tính tỉ số S M O N S A P B khi AM = R 2
d, Tính thể tích của hình do nửa hình tròn đường kính AB quay một vòng quanh AB sinh ra
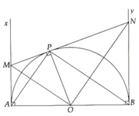
a, Sử dụng các tứ giác nội tiếp chứng minh được P M O ^ = P A O ^ và P N O ^ = P B O ^ => ∆MON và ∆APB đồng dạng (g.g)
b, Theo tính chất hai tiếp tuyến cắt nhau ta có: MP = MA và NP = NB
Mặt khác MP.NP = P O 2 và PO = R Þ AM.BN = R 2 (ĐPCM)
c, Ta có A M = R 2 => M P = R 2
Mặt khác A M = R 2 => BN = 2R => PN = 2R
Từ đó tìm được MN = 5 R 2
Vì DMON và DAPB đồng dạng nên S M O N S A P B = M N A B 2 = 25 16
d, Khi quay nửa đường tròn đường kính AB xung quanh AB ta được hình cầu với tâm O và bán kính R' = OA = R
Thể tích hình cầu đó là V = 4 3 πR 3 (đvdt)
Đúng 0
Bình luận (0)
Cho nửa đường tròn (O) đường kính AB, trên nửa mặt phẳng bờ AB chứa nửa đường tròn đó, kẻ hai tia tiếp tuyến Ax, By với (O). Gọi (I) là đường tròn tiếp xúc với Ax tại C và tiếp xúc ngoài với nửa đường tròn (O) tại F. Kẻ tiếp tuyến CE với (O) (E là tiếp điểm, E khác A), AE cắt tia By tại D. Cho AB 2R.a) Tính AC.BD theo R. Chứng minh CE^2 CF.CB.b) Đường thẳng vuông góc với By tại D cắt OE tại J, CE cắt DF tại G. Chứng minh:- DF là tiếp tuyến của (O).- G là tâm của đường tròn nội tiếp tam giác OI...
Đọc tiếp
Cho nửa đường tròn (O) đường kính AB, trên nửa mặt phẳng bờ AB chứa nửa đường tròn đó, kẻ hai tia tiếp tuyến Ax, By với (O). Gọi (I) là đường tròn tiếp xúc với Ax tại C và tiếp xúc ngoài với nửa đường tròn (O) tại F. Kẻ tiếp tuyến CE với (O) (E là tiếp điểm, E khác A), AE cắt tia By tại D. Cho AB = 2R.
a) Tính AC.BD theo R. Chứng minh CE^2 = CF.CB.
b) Đường thẳng vuông góc với By tại D cắt OE tại J, CE cắt DF tại G. Chứng minh:
- DF là tiếp tuyến của (O).
- G là tâm của đường tròn nội tiếp tam giác OIJ












