Cánh quạt trần quay đều có bán kính 20 cm, quay đều 4 vòng trong 1 giây
a) Tính chu kì, tốc độ góc của một điểm trên mép ngòai cánh quạt?
b) tính tốc độ dài và gia tốc huớng tâm của một điểm trên mép ngoài cánh quạt?
Những câu hỏi liên quan
. Một quạt máy quay đều được 150 vòng trong thời gian 50s. Cánh quạt dài 0,4m. a) Tính chu kì, tần số, tốc độ góc của 1 điểm trên cánh quạt? b) Tính tốc độ dài, gia tốc hướng tâm của 1 điểm nằm mép cánh quạt
Một quạt điện quay đều 360 (vòng/phút) cánh quạt dài 60(cm).Tính tốc độ dài gia tốc hướng tâm của một điểm ở đầu cánh quạt
Giúp mình với ạ!
\(F=360\left(\dfrac{vòng}{ph}\right)=6\left(\dfrac{vòng}{s}\right)\)
\(R=60cm=0,6m\)
Chu kì quay của cánh quạt: \(T=\dfrac{1}{f}=\dfrac{1}{6}s\)
Tốc độ góc: \(\omega=\dfrac{2\pi}{T}=\dfrac{2\pi}{\dfrac{1}{6}}=12\pi\left(\dfrac{rad}{s}\right)\)
Tốc độ dài là: \(v=\omega.R=12\pi.0,6=7,2\pi\left(\dfrac{m}{s}\right)\)
Gia tốc hướng tâm: \(a_{ht}=R.\omega^2=0,6.\left(12\pi\right)^2\approx851,87\left(\dfrac{m}{s^2}\right)\)
Đúng 2
Bình luận (1)
một cánh quạt có bán kính 20cm quay đc 480 vòng trong 4 phút.
a. tính chu kì và tần số của cánh quạt
b. tính tốc độ dài của cánh quạt
Bài 4 .Một cánh quạt may quay được 800 vòng trong 2phút, cánh quạt dài 0,6m . Hãy tính a. chu kỳ và tần số quay ? b. vận tốc dài và vận tốc góc của một điểm trên đầu cánh quạt?
Một đĩa tròn có bán kính 40 cm quay đều một vòng trong 10 giây. Tính gia tốc Hướng Tâm, tốc độ góc, tốc độ dài của điểm A nằm trên vành đĩa đó
Tham khảo:
a.
Chu kì là 0,8s
Tần số là:
v′=ωr′=2,5π.0,4/2=π/2(m/s)
Đúng 1
Bình luận (0)
Một đĩa tròn bán kính 20 cm quay đều quanh trục của nó. Đĩa quay hết một vòng mất 0,2 s. Tìm tốc độ dài v, tốc độ góc ω và gia tốc hướng tâm aht của một điểm nằm trên mép đĩa và cách tâm một khoảng bằng bán kính của đĩa A. v 62,8m/s, ω 31,4rad/s,
a
h
t
≈ 19,7m/
s
2
B. v 3,14m/s, ω 15,7rad/s, ...
Đọc tiếp
Một đĩa tròn bán kính 20 cm quay đều quanh trục của nó. Đĩa quay hết một vòng mất 0,2 s. Tìm tốc độ dài v, tốc độ góc ω và gia tốc hướng tâm aht của một điểm nằm trên mép đĩa và cách tâm một khoảng bằng bán kính của đĩa
A. v = 62,8m/s, ω = 31,4rad/s, a h t ≈ 19,7m/ s 2
B. v = 3,14m/s, ω = 15,7rad/s, a h t ≈ 49m/ s 2
C. v = 6,28m/s, ω = 31,4rad/s, a h t ≈ 197m/ s 2
D. v = 6,28m/s, ω = 3,14rad/s, a h t ≈ 97m/ s 2 .
Chọn đáp án C
+ Tốc độ góc: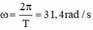 
+ Tốc độ dài: 
+ Gia tốc hướng tâm: 
Đúng 0
Bình luận (0)
Một chất điểm chuyển động tròn đều trên đường tròn tâm O bán kính R = 15 m. Biết chất điểm đó quay 5 vòng hết 31,25 giây. Tính chu kì, tần số, tốc độ dài, tốc độ góc và gia tốc hướng tâm của chuyển động
Xét một cánh quạt trần đang quay tròn đều nếu một điểm trên cánh quạt dịch khỏi vị trí cũ 20 cm thì tốc độ dài của nó tăng 3 lần. Ban đầu điểm đó cách trục quay của quạt bao nhiêu?
Một một quạt máy quay với tần số 240 vòng/phút. Cánh quạt dài 40cm. Tính:Tốc độ góc, tốc độ dài và gia tốc hướng tâm của một điểm ở đầu cánh quạt.
\(f=240\)vòng/phút=4vòng/s
\(\Rightarrow\)Chu kì: \(T=\dfrac{1}{f}=\dfrac{1}{4}s\)
Tốc độ góc: \(\omega=\dfrac{2\pi}{T}=\dfrac{2\pi}{\dfrac{1}{4}}=8\pi\)(rad/s)
Tốc độ dài: \(v=\omega\cdot R=8\pi\cdot0,4=10,05\)m/s
Gia tốc hướng tâm:
\(a_{ht}=r\cdot\omega^2=0,4\cdot\left(8\pi\right)^2\approx252,66\)m/s2
Đúng 4
Bình luận (0)
Một đĩa tròn có đường kính 30cm quay đều quanh trục đối xứng của nó. Trong một phút, đĩa quay được 60 vòng. a. Tính chu kì, tần số và tần số góc của đĩa. b. Tính tốc độ dài và gia tốc hướng tâm của một điểm trên vành đĩa. c. Tính tốc độ dài và gia tốc hướng tâm của một điểm cách vành đĩa 10cm.
Đổi 30 cm =0,3 m; 1 phút =60s
a,\(T=\dfrac{1}{f}=\dfrac{1}{\dfrac{N}{t}}=\dfrac{1}{\dfrac{60}{60}}=1\left(s\right)\)
\(\omega=\dfrac{2\pi}{T}=2\pi\left(\dfrac{rad}{s}\right)\)
b,\(v=\dfrac{2\pi}{T}\cdot r=0,6\pi\left(\dfrac{m}{s}\right)\)
\(a_{ht}=\dfrac{v^2}{r}=\dfrac{\left(0,6\pi\right)^2}{0,3}=1,2\pi^2\left(\dfrac{m}{s^2}\right)\)
c, Đổi 10 cm =0,1m
Khoảng cách từ tâm đến điểm được xét =0,3-0,1=0,2(m)
<Rùi tính tiếp>
\(v'=\dfrac{2\pi}{T}r'=0,4\pi\left(\dfrac{m}{s}\right)\)
\(a_{ht}'=\dfrac{v'^2}{r'}=\dfrac{\left(0,4\pi\right)^2}{0,3}=\dfrac{8}{15}\pi^2\left(\dfrac{m}{s^2}\right)\)
Đúng 2
Bình luận (1)