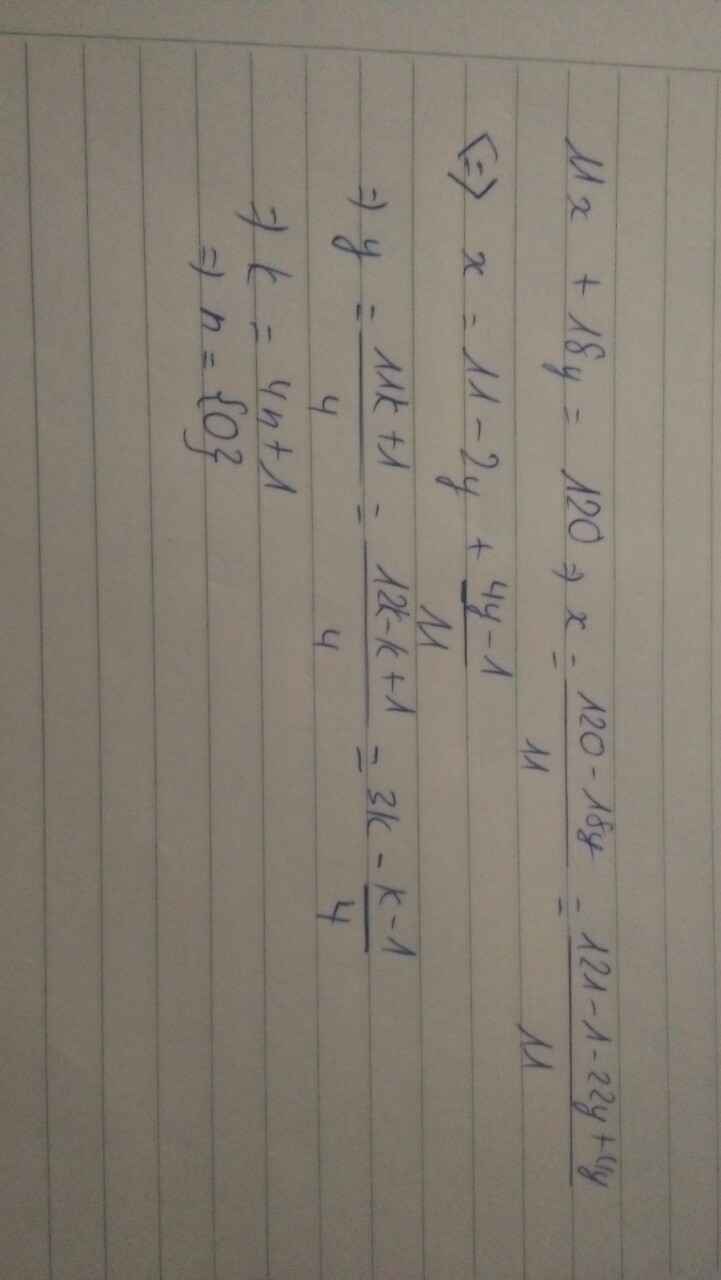Tìm số nguyên x , y thỏa mãn \(y^2+2xy-11x=30\)

Những câu hỏi liên quan
Tìm số nguyên x ; y thoả mãn :
y2 +2xy-11x=30
C1:\(y^2+2xy-11x=30\)
\(\Leftrightarrow4y^2+8xy-44x=120\)
\(\Leftrightarrow4y^2+8xy+4x^2-4x^2-44x-120=0\)
\(\Leftrightarrow4\left(y+x\right)^2-\left(2x\right)^2-2.2x.11-121+1=0\)
\(\Leftrightarrow4\left(y+x\right)^2-\left(2x+11\right)^2+1=0\)
Tự lm tiếp
C2:\(y^2-30=x\left(11-2y\right)\)
\(\Leftrightarrow x=\frac{y^2-30}{11-2y}\)
Vì \(x\in Z\Rightarrow4y^2-120⋮2y-11\)(1)
\(\Leftrightarrow4y^2-121+1⋮2y-11\)
Do \(4y^2-121=\left(2y-11\right)\left(2y+11\right)⋮\left(2y-11\right)\)
\(\Rightarrow1⋮2y+11\)
\(\Leftrightarrow2y+11\inƯ\left(1\right)=\left(\pm1\right)\)
\(\Leftrightarrow y\in\left(-5;-6\right)\)
Thay vô tìm x rồi thay x,y vào xem có tm ko, vì ở(1) nhân thêm 4 chỉ là hệ quả thôi
Đúng 0
Bình luận (0)
Bài 1.
a) Tìm x, y nguyên thỏa mãn: (x + y + 1) ^ 3 = 7 + x ^ 3 + y ^ 3
b) Tìm x, y nguyên dương thỏa mãn: y ^ 2 + 2xy - 8x ^ 2 - 5x = 2
a) \(\left(x+y+1\right)^3=x^3+y^3+7\)
\(\Leftrightarrow\left(x+y\right)^3+3\left(x+y\right)\left(x+y+1\right)+1=x^3+y^3+7\)
\(\Leftrightarrow x^3+y^3+3xy\left(x+y\right)+3\left(x+y\right)\left(x+y+1\right)+1=x^3+y^3+7\)
\(\Leftrightarrow3\left(x+y\right)\left(x+y+xy+1\right)=6\)
\(\Leftrightarrow\left(x+y\right)\left[x\left(1+y\right)+1+y\right]=2\)
\(\Leftrightarrow\left(x+1\right)\left(y+1\right)\left(x+y\right)=2\)
\(\Rightarrow x+1,y+1,x+y\) là các ước của 2.
Ta thấy 6 có 2 dạng phân tích thành tích 3 số nguyên là \(\left(2;1;1\right)\) và\(\left(2;-1;-1\right)\).
- Xét trường hợp \(\left(2;1;1\right)\). Ta có 3 trường hợp nhỏ:
\(\left\{{}\begin{matrix}x+1=2\\y+1=1\\x+y=1\end{matrix}\right.\) ; \(\left\{{}\begin{matrix}x+1=1\\y+1=2\\x+y=1\end{matrix}\right.\) ; \(\left\{{}\begin{matrix}x+1=1\\y+1=1\\x+y=2\end{matrix}\right.\)
Giải ra ta có \(\left(x,y\right)=\left(1;0\right),\left(0;1\right)\).
- Xét trường hợp \(\left(2;-1;-1\right)\). Ta có 3 trường hợp nhỏ:
\(\left\{{}\begin{matrix}x+1=2\\y+1=-1\\x+y=-1\end{matrix}\right.\) ; \(\left\{{}\begin{matrix}x+1=-1\\y+1=2\\x+y=-1\end{matrix}\right.\) ; \(\left\{{}\begin{matrix}x+1=-1\\y+1=1\\x+y=2\end{matrix}\right.\).
Giải ra ta có: \(\left(x;y\right)=\left(1;-2\right),\left(-2;1\right)\).
Vậy \(\left(x;y\right)=\left(0;1\right),\left(1;0\right),\left(1;-2\right),\left(-2;1\right)\)
Đúng 3
Bình luận (1)
b) \(y^2+2xy-8x^2-5x=2\)
\(\Leftrightarrow\left(x^2+2xy+y^2\right)-\left(9x^2+5x\right)=2\)
\(\Leftrightarrow\left(x+y\right)^2-9\left(x^2+\dfrac{5}{9}x+\dfrac{25}{324}\right)+\dfrac{25}{36}=2\)
\(\Leftrightarrow\left(x+y\right)^2-9\left(x+\dfrac{5}{18}\right)^2=\dfrac{47}{36}\)
\(\Leftrightarrow6^2.\left(x+y\right)^2-3^2.6^2\left(x+\dfrac{5}{18}\right)^2=47\)
\(\Leftrightarrow\left(6x+6y\right)^2-\left(18x+5\right)^2=47\)
\(\Leftrightarrow\left(6x+6y-18x-5\right)\left(6x+6y+18x+5\right)=47\)
\(\Leftrightarrow\left(6y-12x-5\right)\left(24x+6y+5\right)=47\)
\(\Rightarrow\)6y-12x-5 và 24x+6y+5 là các ước của 47.
Lập bảng:
| 6y-12x-5 | 1 | 47 | -1 | -47 |
| 24x+6y+5 | 47 | 1 | -47 | -1 |
| x | 1 | \(\dfrac{-14}{9}\left(l\right)\) | \(\dfrac{-14}{9}\left(l\right)\) | 1 |
| y | 3 | \(\dfrac{50}{9}\left(l\right)\) | \(-\dfrac{22}{9}\left(l\right)\) | -5 |
Vậy pt đã cho có 2 nghiệm (x;y) nguyên là (1;3) và (1;-5)
Đúng 2
Bình luận (0)
a) Tìm cặp số nguyên (x;y) thỏa mãn:x-y-6=2xy
b) Tìm mọi số nguyên tố x,y thỏa mãn: x2- 2y2=1
Tìm các số nguyên dương x,y thỏa mãn 11x + 18y = 120
tìm các số nguyên x y thỏa mãn 2xy^2+x+y+1=x^2+2y^2+xy
Tìm các cặp số nguyên \(\left(x;y\right)\) thỏa mãn \(y^2+2xy-3x-2=0\)
\(y^2+2xy-3x-2=0\)
\(\Leftrightarrow\left(y^2+2xy+x^2\right)-\left(x^2+3x+2\right)=0\)
\(\Leftrightarrow\left(x+y\right)^2=\left(x+1\right)\left(x+2\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}x+1=0\\x+2=0\end{matrix}\right.\)
Nếu \(x+1=0\) thì \(\left\{{}\begin{matrix}x=-1\\y=1\end{matrix}\right.\).
Nếu \(x+2=0\) thì \(\left\{{}\begin{matrix}x=-2\\y=2\end{matrix}\right.\)
Thử lại, ta thấy thỏa mãn. Vậy ta tìm được các cặp số \(\left(x;y\right)\) thỏa mãn đề bài là \(\left(-1;1\right),\left(-2;2\right)\)
Đúng 2
Bình luận (0)
Tìm số nguyên x;y;z thỏa mãn:
2.x^2-2xy=5x +y -19
Tìm các số nguyên \(x,y\) thỏa mãn: \(x^2+2xy+7\left(x+y\right)+2y^2+10=0\)
\(x^2+2xy+7.\left(x+y\right)+2y^2+10=0\)
\(\Leftrightarrow\left(x+y^2\right)+7.\left(x+y\right)+\dfrac{49}{4}+y^2-\dfrac{9}{4}=0\)
\(\Leftrightarrow\left(x+y+\dfrac{7}{2}^2\right)=\dfrac{9}{4}-y^2\)
\(Do\left(x+y+\dfrac{7}{2}^2\right)\ge0\Rightarrow\dfrac{9}{4}-y^2\ge0\Rightarrow y^2\le\dfrac{9}{4}\)
Mà y nguyên \(\Rightarrow\left\{{}\begin{matrix}y^2\\\\y^2=1\end{matrix}\right.=0\)
Thay vào phương trình đầu:
Với \(y=0\Rightarrow x^2+7x+10=0\Rightarrow\left\{{}\begin{matrix}x=-2\\\\\\x=-5\end{matrix}\right.\)
Với \(y=1\Rightarrow x^2+9x+19=0\Rightarrow\) không có x nguyên
Với \(y=-1\Rightarrow x^2+5x+5=0\Rightarrow\) không có x nguyên
Đúng 3
Bình luận (0)
Tìm các số nguyên x,y thỏa mãn: 2xy-x-y = 2
<=> 4xy-2x-2y=4
<=> 4xy-2x-2y+1=5
<=> 2x(2y-1) -(2y-1)=5
<=> (2x-1)(2y-1)=5
Suy ra bảng sau:
| 2x-1 | 1 | 5 | -1 | -5 |
| 2y-1 | 5 | 1 | -5 | -1 |
=>
| x | 1 | 3 | 0 | -2 |
| y | 3 | 1 | -2 | 0 |
Vậy (x,y)= (1,3);(3,1);(0,-2);(-2,0) thì thỏa mãn đề bài
tìm các số nguyên dương x,y thỏa mãn 11x+18y=120
y = 7 - 4k +k - 13 Lại đặt k - 13 = t với t nguyên => k = 3t + 1 . Do đó : = 7 - 4 ( 3t + 1) +t = 3 - 11 = tx = 6k = 6 ( 3t+1) = 18t + 6 Thay các biểu thức của x và y vào (1), phương trình đượ c nghiệm đúng. Vậy các nghiệm nguyên của (1) đượ c biểu thị bở i công thức : {=18t+6y=3−11t vớ i t là số nguyên tùy ý mk nha các bạn !!!
Đúng 0
Bình luận (2)
\(11x+18y=120\Rightarrow x=\dfrac{120-18y}{11}=\dfrac{121-1-22y+4y}{11}\)\(\Leftrightarrow x=11-2y+\dfrac{4y-1}{11}\)
\(\left\{{}\begin{matrix}\dfrac{4y-1}{11}=k\\11k=4y-1\end{matrix}\right.\) \(\Rightarrow y=\dfrac{11k+1}{4}=\dfrac{12k-k+1}{4}=3k-\dfrac{k-1}{4}\)
\(\left\{{}\begin{matrix}\dfrac{k-1}{4}=n\\4n=k-1\end{matrix}\right.\) \(\Rightarrow k=4n+1\)
\(\Rightarrow\left\{{}\begin{matrix}y=3.\left(4n+1\right)-n=11n+3\\x=11-2\left(11n+3\right)+4n+1=6-18n\end{matrix}\right.\)
\(x,y>0\Rightarrow\left\{{}\begin{matrix}6-18n>0\\11n+3>0\end{matrix}\right.\) \(\left\{{}\begin{matrix}n< \dfrac{6}{18}\\n>\dfrac{-3}{11}\end{matrix}\right.\) \(\Rightarrow n=\left\{0\right\}\)
Nghiệm duy nhất của phương trình là:
\(\left\{{}\begin{matrix}x=6\\y=3\end{matrix}\right.\)
Đúng 0
Bình luận (0)