chứng minh rằng x0=1(x khác 0)

Những câu hỏi liên quan
chứng minh rằng nếu x0 một nghiệm của đa thức P(x) =ax+b (a khác 0) thì P(x) = a(x-x0)
Cho hai đa thức f(x)=ax^2+bx+c và g(x)=cx^2+bx+a.Chứng minh rằng: Nếu f(x0)=0 thì g(1/x0)=0 (với x0 khác 0)
Chứng minh rằng phương trình x 3 + x - 1 = 0 có nghiệm duy nhất x 0 thỏa mãn 0 < x 0 < 1 2
- Xét hàm số f ( x ) = x 3 + x - 1 , ta có f(0) = -1 và f(1) = 1 nên: f(0).f(1) < 0.
- Mặt khác: f ( x ) = x 3 + x - 1 là hàm đa thức nên liên tục trên [0;1].

- Suy ra f ( x ) = x 3 + x - 1 đồng biến trên R nên phương trình x 3 + x - 1 = 0 có nghiệm duy nhất x 0 ∈ ( 0 ; 1 ) .
- Theo bất đẳng thức Côsi:
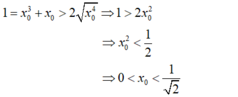
Đúng 0
Bình luận (0)
Cho khoảng K,
x
0
∈
K
và hàm số y f(x) xác định trên
K
x
0
Chứng minh rằng nếu
lim
x
→
x
0
f
(
x
)
+
∞
t...
Đọc tiếp
Cho khoảng K, x 0 ∈ K và hàm số y = f(x) xác định trên K \ x 0
Chứng minh rằng nếu lim x → x 0 f ( x ) = + ∞ thì luôn tồn tại ít nhất một số c thuộc sao cho f(c) > 0
Vì 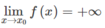
nên với dãy số ( x n ) bất kì, x n ∈ K \ x 0 và x n → x 0 ta luôn có
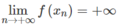
Từ định nghĩa suy ra f ( x n ) có thể lớn hơn một số dương bất kì, kể từ một số hạng nào đó trở đi.
Nếu số dương này là 1 thì f ( x n ) > 1 kể từ một số hạng nàođó trởđi.
Nói cách khác, luôn tồn tạiít nhất một số x k ∈ K \ x 0 sao cho f ( x k ) > 1 .
Đúng 0
Bình luận (0)
a,Cho đa thức f(x)=ax+b (a khác 0). Biết f(0)=0, chứng minh rằng F(x)=-f(-x)với mọi x
b,Đa thức f(x)=ax^2=bx+c (a khác 0).Biết F(1)=F(-1), chứng minh rằng f(x) với mọi x
ĐK: x≥0, x khác 1 Chứng minh rằng 0<A<2
Chứng minh rằng số x0=\(\sqrt{2+\sqrt{2+\sqrt{3}}}-\sqrt{6-3\sqrt{2+\sqrt{3}}}\)là 1 nghiệm của pt x\(x^4+16^2+32=0\)
Cho hàm số y f(x) xác định trên khoảng (a; b) chứa điểm
x
0
Chứng minh rằng nếu
lim
x
→
x
0
f
(
x
)
-
f
(
x...
Đọc tiếp
Cho hàm số y = f(x) xác định trên khoảng (a; b) chứa điểm x 0
Chứng minh rằng nếu lim x → x 0 f ( x ) - f ( x 0 ) x - x 0 = L thì hàm số f(x) liên tục tại điểm x 0
Đặt g ( x ) = f ( x ) - f ( x 0 ) x - x 0 - L và biểu diễn f(x) qua g(x)
Đặt 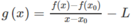
Suy ra g(x) xác định trên
(
a
;
b
)
\
x
0
và 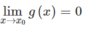
Mặt khác, f ( x ) = f ( x 0 ) + L ( x − x 0 ) + ( x − x 0 ) g ( x ) nên
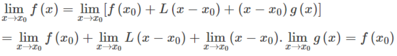
Vậy hàm số y = f(x) liên tục tại
Đúng 0
Bình luận (0)
2) Cho hai đa thức: f(x) = ax2 + bx + c và g(x) = cx2 + bx + a
Chứng minh rằng: Nếu f(x0) = 0 thì g(1/x0) = 0 (với x0 khác 0)









