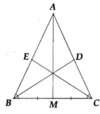
a) Chứng minh được ∆ A M B   =   ∆ A M C  (c.c.c).

Từ đó suy ra AM là tia phân giác của góc BAC.

b) Xét tam giác ABC có AM, BD,CE là các tia phân giác. Từ tính chất ba đường phân giác trong tam giác, suy ra ba đường thẳng AM,BD,CE đồng quy.

DF//BC nhé

a/ Ta có

\(AD\perp OA\) (AD là tiếp tuyến)

O là tâm đường tròn ngoại tiếp \(\Delta ABC\) => AO là trung tuyến của \(\Delta ABC\Rightarrow BC\perp AO\)  (trong tg cân đường trung tuyến xuất phát từ đỉnh đồng thời là đường cao)

=> AD//BC (cùng vuông góc với OA); mà AD=BC (gt) => ABCD là hình bình hành ( Tứ giác có 1 cặp cạnh đối // và bằng nhau thì tứ giác đó là hình bình hành)

b/ Do ABCD là hình bình hành nên AC cắt BD tại trung điểm mỗi đường

Mặt khác ta cũng có OM đi qua trung điểm của AC (Hai tiếp tuyến cùng xuất phát từ 1 điểm thì đường nối điểm đó với tâm đường tròn thì vuông góc và chia đôi dây cung nối 2 tiếp điểm)

=> AC; BD; OM đồng quy

) Có:

a) 

Vì vậy AD = BC và AD//BC nên tứ giác ABCD là hình bình hành.
b) Theo tứ giác ABCD là hình thành nên BD và AC cắt nhau tại trung điểm của mỗi đường.
Theo tính chất của hai tiếp tuyến cắt nhau thì MA=MC và OM là tia phân giác góc AMC.
AM = MC nên tam giác AMC cân tại M và MO là tia phân giác của tam giác AMC nên OM cũng đi qua trung điểm của AC.
Suy ra ba đường thẳng AC, BD, OM đồng quy.

a) Có:

\widehat{MAC}=\dfrac{1}{2}sđ\stackrel\frown{AC}MAC=21​sđAC⌢, \widehat{ACB}=\dfrac{1}{2}sđ\stackrel\frown{AB}.ACB=21​sđAB⌢.

Mà sđ\stackrel\frown{AB}=sđ\stackrel\frown{AC}sđAB⌢=sđAC⌢

Vì vậy AD = BC và AD//BC nên tứ giác ABCD là hình bình hành.
b) Theo tứ giác ABCD là hình thành nên BD và AC cắt nhau tại trung điểm của mỗi đường.
Theo tính chất của hai tiếp tuyến cắt nhau thì $MA=MC$ và OM là tia phân giác góc AMC.
AM = MC nên tam giác AMC cân tại M và MO là tia phân giác của tam giác AMC nên OM cũng đi qua trung điểm của AC.
Suy ra ba đường thẳng AC, BD, OM đồng quy.

mik cho gợi ý thôi né :cậu c/m cho :

S2=S5      => S1=S4

Mà S tam giác ABM=S tam giác AMC=/2S tam giác ABC

C/m :S1+S2+S3 =S4+S5+S6=1/2 S tam giác ABC 

=> Đpcm

Chúc bạn học tốt nha!

a: Xét ΔBFC và ΔCEB có

BF=CE

\(\widehat{FBC}=\widehat{ECB}\)

BC chung

Do đó: ΔBFC=ΔCEB

b: Ta có: ΔABC cân tại A

mà AM là đường trung tuyến ứng với cạnh đáy BC

nên AM là đường cao ứng với cạnh BC

Ta có: ΔBFC=ΔCEB

nên \(\widehat{BFC}=\widehat{CEB}\)

mà \(\widehat{CEB}=90^0\)

nên \(\widehat{BFC}=90^0\)

Xét ΔABC có 

AM là đường cao ứng với cạnh BC

BE là đường cao ứng với cạnh AC

CF là đường cao ứng với cạnh AB

Do đó: AM,BE,CF đồng quy

a) Xét tam giác BFC và CEB ta có: 

Góc FBC = góc ECB

BF = CE

BC cạnh chung 

=> tam giác BFC = tam giác CEB (c-g-c)

a) Xét ΔBFC và ΔCEB có:

BF=EC(gt)

\(\widehat{FBC}=\widehat{ECB}\)(tam giác ABC cân tại A)

BC chung

=> ΔBFC=ΔCEB(c.g.c)

b) Xét tam giác ABC cân tại A có

AM là đường trung tuyến 

=> AM là đường cao của tam giác ABC(1)

Ta có: ΔBFC=ΔCEB(cmt)

\(\Rightarrow\widehat{BFC}=\widehat{BEC}=90^0\)

=> CF là đường cao của tam giác ABC(2)

Từ (1),(2) và BE là đường cao của tam giác ABC

=> BE,,CF,AM đồng quy