Cho điểm C thuộc đoạn AB, . Vẽ về môt phía của AB các nửa đường tròn có đường kính theo thứ tự là AC, AB. Tính bán kính của đường tròn (I) tiếp xúc với các nửa đường tròn trên và tiếp xúc với đoạn thẳng AB

Những câu hỏi liên quan
Cho nửa đường tròn đường kính AB, C là một điểm thuộc bán kính OA. Đường vuông góc với AB cắt nữa đường tròn tại D, đường tròn tâm I tiếp xúc với nửa đường tròn và tiếp xúc với các đoạn thẳng CA, CD. Gọi E là tiếp điểm trên AC của đường tròn tâm I. Chứng minh BD=BE
Cho B nằm giữa A và C sao cho AB=14cm BC=28cm. Vẽ về một phía của ac các nửa đường tròn tâm I, K, O có đường kính lần lượt là AB, BC, CA. tính bán kinh suc ả đường tròn tâm M tiếp xúc ngoài với các nửa đường tròn (I), (K) và tiếp xúc trong với nauwr đường tròn (O)
Cho đoạn thẳng AB, điểm C nằm giữa AB. Vẽ về một phía của AB các nửa đường tròn có đường kính theo thứ tự là AB, AC, BC. Đường vuông góc với AB tại C cắt nửa đường tròn lớn hơn tại D. DA, DB cắt các nửa đường tròn có đường kính AC, BC theo thứ tự tại M, N. Chứng minh rằng MN là tiếp tuyến chung của các nửa đường tròn có đường kính AC, BC
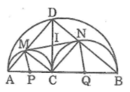
Gọi P là trung điểm của AC, Q là trung điểm của BC, I là giao điểm của MN với DC
Vì CMDN là hình chữ nhật nên IC = IM = ID = IN
Tam giác CNI cân tại I nên ![]() (3)
(3)
Tam giác CNQ cân tại Q nên ![]() (4)
(4)
Vì AB ⊥ CD nên ![]() =
90
°
(5)
=
90
°
(5)
Từ (3), (4) và (5) suy ra: ![]() =
90
°
hay MN ⊥ QN
=
90
°
hay MN ⊥ QN
Vậy MN là tiếp tuyến của đường tròn đường kính BC
Tam giác CMI cân tại I nên 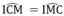 (6)
(6)
Tam giác CMP cân tại P nên 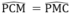 (7)
(7)
Vì AB ⊥ CD nên 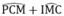 =
90
°
(8)
=
90
°
(8)
Từ (6), (7) và (8) suy ra: 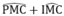 =
90
°
hay MN ⊥ PM
=
90
°
hay MN ⊥ PM
Vậy MN là tiếp tuyến của đường tròn đường kính AC
Đúng 0
Bình luận (0)
Cho đoạn thẳng AB và 1 điểm C trên AB với ACa, BCb. Đường thẳng đi qua C và vuông góc với AB cắt nửa đường tròn đường kính AB tại P. Dựng đường tròn tâm P bán kính r1, tiếp xúc với CA,CD và tiếp xúc với nửa đường tròn đường kính AB. Dựng đường tròn tâm Q bán kính r2 tiếp xúc với CB,CD và tiếp xúc với nửa đường tròn đường kính AB. Gọi r là bán kính đường tròn nội tiếp tam giác ABDa/ Tính r1,r2 theo a,bb/Tìm đẳng thức liên hệ giữa r,r1,r2
Đọc tiếp
Cho đoạn thẳng AB và 1 điểm C trên AB với AC=a, BC=b. Đường thẳng đi qua C và vuông góc với AB cắt nửa đường tròn đường kính AB tại P. Dựng đường tròn tâm P bán kính r1, tiếp xúc với CA,CD và tiếp xúc với nửa đường tròn đường kính AB. Dựng đường tròn tâm Q bán kính r2 tiếp xúc với CB,CD và tiếp xúc với nửa đường tròn đường kính AB. Gọi r là bán kính đường tròn nội tiếp tam giác ABD
a/ Tính r1,r2 theo a,b
b/Tìm đẳng thức liên hệ giữa r,r1,r2
Cho đoạn thẳng AB, điểm C nằm giữa A và B. Vẽ về một phía của AB các nửa đường tròn có đường kính theo thứ tự là AB, AC, CB. Đường vuông góc với AB tại C cắt nửa đường tròn lớn tại D. DA, DB cắt các nửa đường tròn có đường kính AC, CB theo thứ tự tại M, N
a) Tứ giác DMCN là hình gì ? Vì sao ?
b) Chứng minh hệ thức DM.DA = DN.DB
a: góc AMC=1/2*180=90 độ
=>góc DMC=90 độ
góc CNB=1/2*180=90 độ
=>góc DNC=90 độ
Kẻ tiếp tuyến Cx của hai đường tròn đường kính AC,CB, Cx cắt MN tại I
Xét (E) có
IC,IM là tiếp tuyến
=>IC=IM
Xét (F) có
IN,IC là tiếp tuyến
=>IN=IC=IM
Xét ΔMCN có
CI là trung tuyến
CI=MN/2
=>ΔMCN vuông tại C
góc DMC=góc DNC=góc MCN=90 độ
=>DMCN là hcn
b: ΔDCA vuông tại C có CM vừa là đường cao
nên DM*DA=DC^2
ΔDCB vuông tại C có CN là đường cao
nên DN*DB=DC^2=DM*DA
Đúng 0
Bình luận (0)
Cho nửa đường tròn tâm O có đường kính AB. Vẽ các tiếp tuyến Ax, By (Ax, By và nửa đường tròn thuộc cùng một mặt phẳng bờ AB). Gọi M là một điểm bất kì thuộc nửa đường tròn. Tiếp tuyến tại M cắt Ax, By theo thứ tự ở C và D. Chứng minh rằng đường tròn có đường kính CD tiếp xúc với AB
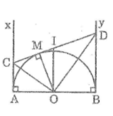
Theo tính chất tiếp tuyến, ta có:
Ax ⊥ AB
By ⊥ AB
Suy ra: Ax // By hay AC // BD
Suy ra tứ giác ABDC là hình thang
Gọi I là trung điểm của CD
Khi đó OI là đường trung bình của hình thang ABDC
Suy ra: OI // AC ⇒ OI ⊥ AB
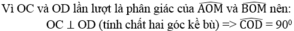
Suy ra: IC = ID = IO = (1/2).CD (tính chất tam giác vuông)
Suy ra I là tâm đường tròn đường kính CD. Khi đó O nằm trên đường tròn tâm I đường kính CD và IO vuông góc với AB tại O.
Vậy đường tròn có đường kính CD tiếp xúc với AB tại O.
Đúng 0
Bình luận (0)
Cho nửa đường tròn tâm O đường kính AB. Điểm C nằm trên O;A. (I) tiếp xúc với nửa đường tròn (O)và tiếp xúc với các đoạn thẳng CA, CD. Gọi E là tiếp điểm của AC với (I). Chứng minh: BD=BE
cho đoạn thẳng AB, điểm C nằm giữa A và B.Vẽ về một phía của AB các nửa đường tròn có đường kính theo thứ tự là AB,AC,CB.Đường thẳng vuông góc với AB tại C cắt nửa đường tròn lớn tại D . DA, BD cắt các nửa đường tròn có đường kính AC, CB theo thứ tự tại M và Na)tứ giác DMCN là hình gì? vì sao?b) chứng minh hệ thức DM.DA DN.DBc) Chứng minh rằng MN là tiếp tuyến chung của các nửa đường tròn có đường kính AC và CB.
Đọc tiếp
cho đoạn thẳng AB, điểm C nằm giữa A và B.Vẽ về một phía của AB các nửa đường tròn có đường kính theo thứ tự là AB,AC,CB.Đường thẳng vuông góc với AB tại C cắt nửa đường tròn lớn tại D . DA, BD cắt các nửa đường tròn có đường kính AC, CB theo thứ tự tại M và N
a)tứ giác DMCN là hình gì? vì sao?
b) chứng minh hệ thức DM.DA= DN.DB
c) Chứng minh rằng MN là tiếp tuyến chung của các nửa đường tròn có đường kính AC và CB.
Cho đoạn thẳng AB, điểm C nằm giữa A và B. Vẽ về một phía của AB các nửa đường tròn có đường kính theo thứ tự là AB, AC, CB. Đường vuông góc với AB tại C cắt nửa đường tròn lớn tại D. DA, DB cắt các nửa đường tròn có đường kính AC, CB theo thứ tự tại M, N
a) Tứ giác DMCN là hình gì ? Vì sao ?
b) Chứng minh hệ thức DM.DA DN.DB
c) Chứng minh MN là tiếp tuyến chung của các nửa đường tròn có đường kính AC và CB
d*) Điểm C ở vị trí nào trên AB thì MN có độ dài lớn nhất ?
Đọc tiếp
Cho đoạn thẳng AB, điểm C nằm giữa A và B. Vẽ về một phía của AB các nửa đường tròn có đường kính theo thứ tự là AB, AC, CB. Đường vuông góc với AB tại C cắt nửa đường tròn lớn tại D. DA, DB cắt các nửa đường tròn có đường kính AC, CB theo thứ tự tại M, N
a) Tứ giác DMCN là hình gì ? Vì sao ?
b) Chứng minh hệ thức DM.DA = DN.DB
c) Chứng minh MN là tiếp tuyến chung của các nửa đường tròn có đường kính AC và CB
d*) Điểm C ở vị trí nào trên AB thì MN có độ dài lớn nhất ?
















