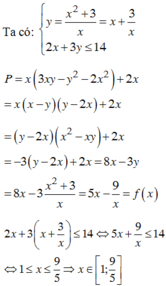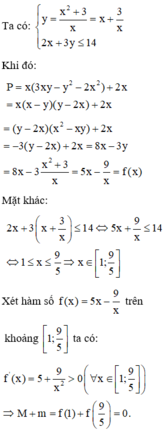Tìm x để biểu thức 3−x2+2x3−x2+2x có giá trị lớn nhất .

Những câu hỏi liên quan
Bài 1: Tìm nghiệm của đa thức sau:
a) A(x)=x2-4x+4
b) B(x)=2x3+x2+2x+1
c) C(x)=|2x-3|- 1/3
Bài 2: Tìm giá trị nhỏ nhất của biểu thức sau:
a) x2-4x+5
b) -100/(x+1)2+10
(GIÚP MÌNH CẢ 2 BÀI NHÉ! )
Bài 2 :
a, \(x^2-4x+4+1=\left(x-2\right)^2+1\ge1\)
Dấu ''='' xảy ra khi x = 2
b, Ta có \(\left(x+1\right)^2+10\ge10\Rightarrow\dfrac{-100}{\left(x+1\right)^2+10}\ge-\dfrac{100}{10}=-10\)
Dấu ''='' xảy ra khi x = -1
Đúng 1
Bình luận (0)
Bài 1 :
a, Ta có \(A\left(x\right)=x^2-4x+4=0\Leftrightarrow\left(x-2\right)^2=0\Leftrightarrow x=2\)
b, \(B\left(x\right)=x^2\left(2x+1\right)+\left(2x+1\right)=\left(x^2+1>0\right)\left(2x+1\right)=0\Leftrightarrow x=-\dfrac{1}{2}\)
c, \(C\left(x\right)=\left|2x-3\right|=\dfrac{1}{3}\Leftrightarrow\left[{}\begin{matrix}2x=\dfrac{1}{3}+3=\dfrac{10}{3}\\2x=-\dfrac{1}{3}+3=\dfrac{8}{3}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5}{3}\\x=\dfrac{4}{3}\end{matrix}\right.\)
Đúng 1
Bình luận (0)
1- Tìm x để biểu thức 3−x2+2x3−x2+2x có giá trị lớn nhất .2- Tìm x để biểu thức 3(2x+9)2−13(2x+9)2−1 có giá trị nhỏ nhất3- Tìm giá trị rút gọn của (x−1)(x+2)−(x+1)x(x−1)(x+2)−(x+1)x4- 511a11711511a11711 . Tìm số a thỏa mãn5- Giá trị nhỏ nhất của M|x+3|+|x-5|6- Giá trị lớn nhất của A|x+13|+647- Bậc của đơn thức 12x2y5z312x2y5z38- (13)2017×32016×21(13)2017×32016×219- Nghiệm của đa thức x2−60x+900x2−60x+90010- Giá trị rút gọn (2x−4)(x+3)−2x(x+1)
Đọc tiếp
1- Tìm x để biểu thức 3−x2+2x3−x2+2x có giá trị lớn nhất .
2- Tìm x để biểu thức 3(2x+9)2−13(2x+9)2−1 có giá trị nhỏ nhất
3- Tìm giá trị rút gọn của (x−1)(x+2)−(x+1)x(x−1)(x+2)−(x+1)x
4- 511<a11<711511<a11<711 . Tìm số a thỏa mãn
5- Giá trị nhỏ nhất của M=|x+3|+|x-5|
6- Giá trị lớn nhất của A=|x+13|+64
7- Bậc của đơn thức 12x2y5z312x2y5z3
8- (13)2017×32016×21(13)2017×32016×21
9- Nghiệm của đa thức x2−60x+900x2−60x+900
10- Giá trị rút gọn (2x−4)(x+3)−2x(x+1)
Cho
x
,
y
∈
R
thỏa mãn điều kiện
2
y
≥
x
2
và
y
≤
-
2
x
3
+
3
x
Tìm giá trị lớn nhất của biểu thức
P
x
2
+
y
2
A. 5 B. 4 C. 3 D. 2
Đọc tiếp
Cho x , y ∈ R thỏa mãn điều kiện 2 y ≥ x 2 và y ≤ - 2 x 3 + 3 x Tìm giá trị lớn nhất của biểu thức P = x 2 + y 2
A. 5
B. 4
C. 3
D. 2
Từ giả thiết bài toán suy ra
y ≥ 0 x 2 2 ≤ - 2 x 2 + 3 x ⇔ y ≥ 0 5 x 2 - 6 x ≤ 0 ⇔ y ≥ 0 0 ≤ x ≤ 6 5
Ta có
x 2 + y 2 ≤ x 2 + - 2 x 2 + 3 x 2 = 4 x 4 - 12 x 3 + 10 x 2
Ta có f ' x = 4 x x - 1 x - 5
f ' x = 0 x = 0 x = 1 x = 5 So điều kiện, chọn x = 0 ; x = 1 ; f(0); f(1) = 2; f 6 5 = 1224 625
Vậy m a x P = 2
Đáp án D
Đúng 0
Bình luận (0)
Tìm các cặp số (x,y) để biểu thức -x2-y2+xy+2x+2y có giá trị lớn nhất
Cho x,y0 và thỏa mãn
x
2
-
x
y
+
3
0
2
x
+
3
y
-...
Đọc tiếp
Cho x,y>0 và thỏa mãn x 2 - x y + 3 = 0 2 x + 3 y - 14 ≤ 0 . Tính tổng giá trị lớn nhất và nhỏ nhất của biểu thức P = 3 x 2 y - x y 2 - 2 x 3 + 2 x ?
A. 8
B. 0
C. 4
D. 12
Ta có:
x 2 - x y + 3 = 0 1 2 x + 3 y - 14 ≤ 0 2
Do x,y>0 nên ⇔ x 2 + 3 x thay vào (2) ta được:
2 x + 3 . x 2 + 3 x - 14 ≤ 0
⇔ 2 x 2 + 3 x 2 + 9 - 14 x x ≤ 0
⇔ 5 x 2 - 14 x + 9 ≤ 0 ⇔ 1 ≤ x ≤ 9 5
Thay y = x 2 + 3 x vào P ta được:
P = 3 x 2 y - x y 2 - 2 x 3 + 2 x
= 3 x 2 . x 2 + 3 x - x . x 2 + 3 x 2 - 2 x 3 + 2 x
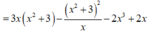
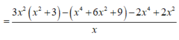
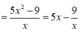
P ' = 5 + 9 x 2 > 0 với mọi x nên hàm số P=P(x) đồng biến trên 1 ; 9 5
Vậy 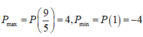
Tổng ![]() .
.
Chọn đáp án B.
Đúng 0
Bình luận (0)
Cho x,y 0 và thỏa mãn
x
2
-
x
y
+
3
0
2
x
+
2
y
-...
Đọc tiếp
Cho x,y > 0 và thỏa mãn x 2 - x y + 3 = 0 2 x + 2 y - 14 ≤ 0 .Tính tổng giá trị lớn nhất và nhỏ nhất của biểu thức P = 3 x 2 y - x y 2 - 2 x 3 + 2 x
A. 4.
B. 8.
C. 12.
D. 0.
Cho
x
,
y
0
và thỏa mãn
x
2
−
x
y
+
3
0
2
x
+
3...
Đọc tiếp
Cho x , y > 0 và thỏa mãn x 2 − x y + 3 = 0 2 x + 3 y − 14 ≤ 0 . Tính tổng giá trị lớn nhất và nhỏ nhất của biểu thức P = 3 x 2 y − x y 2 − 2 x 3 + 2 x ?
A. 4
B. 8
C. 12
D. 0
Cho
x
,
y
0
và thỏa mãn
x
2
-
x
y
+
3
0
2
x
+
3...
Đọc tiếp
Cho x , y > 0 và thỏa mãn x 2 - x y + 3 = 0 2 x + 3 y - 14 ≤ 0 . Tính tổng giá trị lớn nhất và nhỏ nhất của biểu thức P = 3 x 2 y - x y 2 - 2 x 3 + 2 x ?
A. 8
B. 0
C. 4
D. 12
Đáp án B
Phương pháp:
- Rút y từ phương trình đầu, thay vào bất phương trình sau tìm điều kiện của x .
- Thay y ở trên vào biểu thức P đưa về biến x .
- Sử dụng phương pháp hàm số đánh giá P tìm GTLN, GTNN.
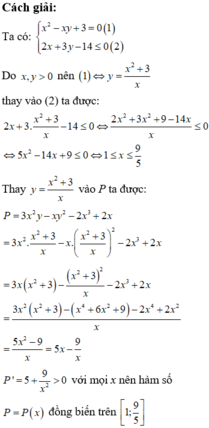
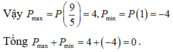
Đúng 0
Bình luận (0)
Cho biểu thức sau:
D
(
x
+
2
)
2
x
.
1
−
x
2
x
+
2
−
x...
Đọc tiếp
Cho biểu thức sau: D = ( x + 2 ) 2 x . 1 − x 2 x + 2 − x 2 + 6 x + 4 x .
a) Tìm điều kiện xác định của biểu thức D;
b) Rút gọn biểu thức D;
c) Tìm giá trị x để D có giá trị lớn nhất.
a) x ≠ 0 , x ≠ − 2
b) Ta có D = x 2 - 2x - 2.
c) Chú ý D = - x 2 - 2x - 2 = - ( x + 1 ) 2 - 1 ≤ -1. Từ đó tìm được giá trị lớn nhất của D = -1 khi x = -1.
Đúng 0
Bình luận (0)
Xét hai số thực x, y thỏa mãn
x
2
+
y
2
2
. Tìm giá trị lớn nhất M của biểu thức
P
2
x
3
+
y
3
-
3
x
y
A.
M
11
2
B.
M...
Đọc tiếp
Xét hai số thực x, y thỏa mãn x 2 + y 2 = 2 . Tìm giá trị lớn nhất M của biểu thức P = 2 x 3 + y 3 - 3 x y
A. M = 11 2
B. M = 13 2
C. M = 15 2
D. M = 17 2
Đáp án B
Ta có P = 2 x 3 + y 3 - 3 x y = 2 x + y x 2 - x y + y 2 - 3 x y = 2 x + y 2 - x y - 3 x y
Mặt khác x 2 + y 2 = 2 ⇔ x + y 2 - 2 x y = 2 ⇔ 2 x y = x + y 2 - 2 ≤ x + y 2 2 ⇔ - 2 ≤ x + y ≤ 2
Khi đó 2 P = 2 x + y 4 - 2 x y - 6 x y = 2 x + y 4 - x + y 2 + 2 - 3 x + y 2 - 2
= 6 + 12 x + y - 3 x + y 2 - 2 x + y 3 = f t = 6 + 12 t - 3 t 2 - 2 t 3
Với t = x + y ∈ - 2 ; 2
Xét hàm số f t = 6 + 12 t - 3 t 2 - 2 t 3 trên đoạn [-2;2] ta có
f ' t = 12 - 6 t - 6 t 2 ; f ' t = 0 ⇔ [ t = - 2 t = 1
So sánh các giá trị f(-2);f(1);f(2), ta được m a x - 2 ; 2 f t = f 1 = 13 ⇒ M = 13 2 .
Đúng 0
Bình luận (0)