Cho tam giác ABC . Gọi D,E lần lượt là trung điểm của AB và AC ; O là một điểm bất kì nằm trong tam giác ABC ; M , N lần lượt là các điểm đối xứng với O qua D,E
Chứng minh M , C đối xứng với nhau qua trung điểm I của đoạn thẳng BN.
Những câu hỏi liên quan
Cho tam giác ABC vuông tại A (AB AC). Gọi D và E lần lượt là trung điểm của BC và AC. a) Chứng minh tứ giác ABDE là hình thang vuôngCho tam giác ABC vuông tại A (AB AC). Gọi D và E lần lượt là trung điểm của BC và ACa) Chứng minh tứ giác ABDE là hình thang vuôngb) Gọi K là điểm đối xứng của A qua D.CHỨNG MINH TỨ GIÁC ABKC LÀ HÌNH CHỮ NHẬTc) Từ A kẻ AH vuông tại BC tại H.Gọi M là trung điểm BH.G là trung điểm của AH,F là trung điểm KC.chứng minh AM vuông góc MF toán 8
Đọc tiếp
Cho tam giác ABC vuông tại A (AB < AC). Gọi D và E lần lượt là trung điểm của BC và AC. a) Chứng minh tứ giác ABDE là hình thang vuôngCho tam giác ABC vuông tại A (AB < AC). Gọi D và E lần lượt là trung điểm của BC và AC
a) Chứng minh tứ giác ABDE là hình thang vuông
b) Gọi K là điểm đối xứng của A qua D.CHỨNG MINH TỨ GIÁC ABKC LÀ HÌNH CHỮ NHẬT
c) Từ A kẻ AH vuông tại BC tại H.Gọi M là trung điểm BH.G là trung điểm của AH,F là trung điểm KC.chứng minh AM vuông góc MF toán 8
a) Chứng minh tứ giác ABDE là hình thang vuông
b) Gọi K là điểm đối xứng của A qua D.CHỨNG MINH TỨ GIÁC ABKC LÀ HÌNH CHỮ NHẬT
c) Từ A kẻ AH vuông tại BC tại H.Gọi M là trung điểm BH.G là trung điểm của AH,F là trung điểm KC.chứng minh AM vuông góc MF toán 8
a: Xét ΔCAB có CE/CA=CD/CB
nên ED//AB và ED=AB/2
=>AEDB là hình thang
mà góc EAB=90 độ
nênAEDB là hình thang vuông
b: Xét tứ giác ABKC có
D là trung điểm chung của AK và BC
góc BAC=90 độ
Do đó: ABKC là hình chữ nhật
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A, gọi M và E lần lượt là trung điểm của BC và AC, kẻ MD vuông góc với AB tại D
cho tam giác ABC vuông tại A,gọi M và E lần lượt là trung điểm của BC và AC,kẻ MD vuông góc với AB tại D.Gọi K là điểm đối xứng với M qua E
a)biết AB6m;AC8cm.Tính BC;AM
b)chứng minh tứ giácADME là hình chữ nhật và tứ giác AMCK là hình thoi
c)kẻ MH vuông góc với AK(H thuộc AK).Chúng minh BC mũ 24HE mũ 2+4HD mũ 2
Đọc tiếp
Cho tam giác ABC vuông tại A, gọi M và E lần lượt là trung điểm của BC và AC, kẻ MD vuông góc với AB tại D
cho tam giác ABC vuông tại A,gọi M và E lần lượt là trung điểm của BC và AC,kẻ MD vuông góc với AB tại D.Gọi K là điểm đối xứng với M qua E
a)biết AB=6m;AC=8cm.Tính BC;AM
b)chứng minh tứ giácADME là hình chữ nhật và tứ giác AMCK là hình thoi
c)kẻ MH vuông góc với AK(H thuộc AK).Chúng minh BC mũ 2=4HE mũ 2+4HD mũ 2
a)biết AB=6m;AC=8cm.Tính BC;AM
b)chứng minh tứ giácADME là hình chữ nhật và tứ giác AMCK là hình thoi
c)kẻ MH vuông góc với AK(H thuộc AK).Chúng minh BC mũ 2=4HE mũ 2+4HD mũ 2
Cho tam giác ABC có BC = 16 cm. Gọi D và E lần lượt là trung điểm của AB và AC. Gọi M và N lần lượt là trung điểm của BD và EC. Tính MN?
A. 9cm
B. 8cm
C. 10cm
D. 12cm
* Xét tam giác ABC có D và E lần lượt là trung điểm của AB và AC nên DE là đường trung bình của tam giác.
Suy ra: DE// BC và
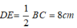
* Xét tứ giác DECB có DE // BC nên DECB là hình thang.
Lại có: M và N lần lượt là trung điểm của BD và EC nên MN là đường trung bình của hình thang .
Chọn đáp án D
Đúng 1
Bình luận (0)
Cho tam giác ABC. Trên tia đối của các tia AB, AC lần lượt lấy các điểm D và E sao cho AD= AB và AE= AC
a) Chứng minh: tam giác ABC= tam giác ADE
b) Chứng minh DE // BC
c) Gọi M, N lần lượt là trung điểm của BC và DE. Chứng minh A là trung điểm của MN
Cho tam giác ABC vuông tại A. Gọi M, N, P lần lượt là trung điểm của ab ac bc. Gọi D, E lần lượt là điểm đối xứng của P qua M và N.a, Tính AP và diện tích tam giác ABC biết AB 6cm, AC 8cm.b, Chứng minh tứ giác AMPN là hình chữ nhật.c, Chúng minh tứ giác APCE là hình thoi.d, Tam giác ABC cần có điều kiện gì để tứ giác APCE là hình vuông?e, Chứng minh AP, BE, CD đồng quy.f, Chứng minh ba điểm D, A, E thẳng hàng.
Đọc tiếp
Cho tam giác ABC vuông tại A. Gọi M, N, P lần lượt là trung điểm của ab ac bc. Gọi D, E lần lượt là điểm đối xứng của P qua M và N.
a, Tính AP và diện tích tam giác ABC biết AB = 6cm, AC = 8cm.
b, Chứng minh tứ giác AMPN là hình chữ nhật.
c, Chúng minh tứ giác APCE là hình thoi.
d, Tam giác ABC cần có điều kiện gì để tứ giác APCE là hình vuông?
e, Chứng minh AP, BE, CD đồng quy.
f, Chứng minh ba điểm D, A, E thẳng hàng.
Cho tam giác ABC có M, N, E lần lượt là trung điểm của BC, AC, AB. Gọi G là trọng tâm của tam giác ABC và D là trung điểm của MN. Chứng minh C, G, E, D thẳng hàng.
bạn tự vẽ hình nhé !
Nối EN, NM, ME. Ta có G là trọng tâm tam giác ABC nên G là giao điểm 3 đường trung tuyến , do đó E, G , C thẳng hàng.(1)
bây giờ chứng minh E,G,D thẳng hàng thì sẽ có C,G,E,D thẳng hàng.
Ta có E là trung điểm AB, N là trung điểm AC suy ra EN là đường trug bình tam giác ABC nên EN =1/2 BC và EN song2 với BC. lại có MC=1/2 BC ( M trug điểm BC)
suy ra EN = CM và EN song2 với CM từ đó ENCM là hình bình hành.
Xét hình bình hành ENCM có D là trung điểm MN suy ra D là trug điểm EC => ED=DC.
Vì G là trọng tâm tam giác ABC nên EG=1/3 EC=2/3ED (vì ED=1/2 EC)
Xét tam gác ENM có ED là trung tuyến , EG=2/3 ED suy ra G là trọng âm tam giác ENM. suy ra EGD thẳng hàng (2)
TỪ 1 và 2 suy ra E,G,D,C thẳng hàng
Đúng 0
Bình luận (0)
Cho tam giác abc, ab=ac. Trên cạnh ab và ac lần lượt lấy 2 điểm m và n sao cho am=an. Gọi e và d lần lượt là trung điểm của mn và bc. Cmr: a d e thẳng hàng
Xét tam giác AMN có AM = AN nên tam giác AMN cân tại A.
Vậy thì trung tuyến AD chính là phân giác của góc \(\widehat{MAN}\)
Xét tam giác ABC có AB = AC nên tam giác ABC cân tại A.
Vậy thì trung tuyến AE chính là phân giác của góc \(\widehat{BAC}\)
Từ đó ta có D, E cùng thuộc tia phân giác của góc A hay A, D, E thẳng hàng.
Đúng 0
Bình luận (0)
cho tam giác abc và m là một điểm thuộc miền trong của tam giác đó. gọi d,e,f lần lượt là trung điểm của ab,ac,bc và a',b',c' là điểm đối xứng của M lần lượt qua tâm đối xứng f,e,d
Cho tam giác ABC có BC=18cm, Gọi D, E lần lượt là trung điểm của AB và AC; M, N lần lượt là trung điểm của BD và CE. Tính MN?
D và E là trung điểm của AB và AC => DE là đường trung bình của tam giác ABC
=> DE//BC và DE=1/2 BC = 9cm
Tứ giác DECB có DE // BC => Hình thang DECB đáy DE, CB
Lại có M, N là trung điểm BD và CE=> MN là đường trung bình của hình thang DECB
=> MN = 1/2 ( DE + BC) = 1/2 (9+18) = 13,5 (cm)
Vậy....................................
________________________JK~ Liên Quân Group ________________________
Đúng 0
Bình luận (0)
Cho tam giác ABC (AB < AC < BC), đường cao AH. Gọi D, E, F lần lượt là trung điểm của các cạnh AB, BC và AC. Gọi I là giao điểm của DF và AE.
b) Chứng I là trung điểm của DF.
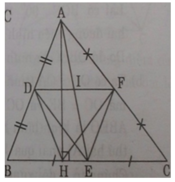
b) Ta có DF // BC (cmt) hay DI // BE; D là trung điểm của AD ⇒ I là trung điểm của AE và DI = BE/2
Trong ΔAEC có IF là đường trung bình nên IF = EC/2 mà EC = EB (gt) ⇒ IF = ID hay I là trung điểm của DF.
Đúng 0
Bình luận (0)