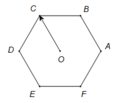
Các vecto cùng phương  O C →  với  có điểm đầu và điểm cuối là các đỉnh của lục giác

: .

Chọn C.

Chọn C.

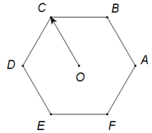
Các vecto cùng phương với  có điểm đầu và điểm cuối là các đỉnh của lục giác : 

Kẻ trung tuyến AM

\(\Rightarrow S_{ABM}=S_{ACM}=\dfrac{1}{2}S_{ABC}=15\left(cm^2\right)\)

Lại có \(\dfrac{MG}{AG}=\dfrac{1}{3}\Rightarrow\dfrac{S_{BGM}}{S_{ABM}}=\dfrac{S_{CGM}}{S_{ACM}}=\dfrac{MG}{AG}=\dfrac{1}{3}\)

\(\Rightarrow S_{BGM}=S_{CGM}=\dfrac{1}{3}\cdot S_{ABM}=5\left(cm^2\right)\\ \Rightarrow S_{BGC}=S_{BGM}+S_{CGM}=10\left(cm^2\right)\)

Lời giải:
Gọi $AE$ là đường trung tuyến của tam giác $ABC$ thì $E$ là trung điểm của $BC$

\(\overrightarrow{BA}=\overrightarrow{BC}+\overrightarrow{GA}=\overrightarrow{BC}+2\overrightarrow{EG}\\ =\overrightarrow{BC}+2(\overrightarrow{EC}+\overrightarrow{CG})\\ =\overrightarrow{BC}+2\overrightarrow{EC}+2\overrightarrow{CG}\\ =\overrightarrow{BC}+\overrightarrow{BC}-2\overrightarrow{GC}\\ =2\overrightarrow{BC}-2\overrightarrow{GC}\)

Ko nha bạn

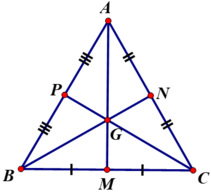
- Gọi G là trọng tâm ΔABC đều

AM, BN, CP là các đường trung tuyến của ΔABC

Theo tính chất trọng tâm tam giác :

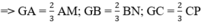
Vì ΔABC đều nên ba trung tuyến AM = BN = CP (áp dụng chứng minh bài 29)

Suy ra: GA = GB = GC

Và AM – GA = BN – GB = CP – GC hay GM = GN = GP

- ΔANG và ΔCNG

GN chung

GA = GC (chứng minh trên)

NA = NC ( N là trung điểm AC)

⇒ ΔANG = ΔCNG (c.c.c)

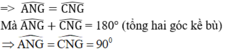
⇒ GN ⊥ AC tức là GN là khoảng cách từ G đến AC.

Chứng minh tương tự GM, GP là khoảng cách từ G đến BC, AB.

- Mà GM = GN = GP (chứng minh trên)

Vậy G cách đều ba cạnh của tam giác ABC.