1)

\((x+2)(x+3)(x+4)(x+5)-24\\=[(x+2)(x+5)]\cdot[(x+3)(x+4)]-24\\=(x^2+7x+10)(x^2+7x+12)-24\)

Đặt \(x^2+7x+10=y\), khi đó biểu thức trở thành:

\(y(y+2)-24\\=y^2+2y-24\\=y^2+2y+1-25\\=(y+1)^2-5^2\\=(y+1-5)(y+1+5)\\=(y-4)(y+6)\\=(x^2+7x+10-4)(x^2+7x+10+6)\\=(x^2+7x+6)(x^2+7x+16)\)

2) Bạn xem lại đề!

a, Ta có \(\Delta=\left(-3\right)^2-4.\left(-1\right).2=9+8=17>0\)

Nên pt có 2 nghiệm phân biệt 

\(x_1=\frac{3-\sqrt{17}}{4};x_2=\frac{3+\sqrt{17}}{4}\)

b,A/D hệ thức vi et ta có 

\(\hept{\begin{cases}x_1+x_2=\frac{3}{2}\\x_1x_2=-\frac{1}{2}\end{cases}}\)

ý cậu như nào >?

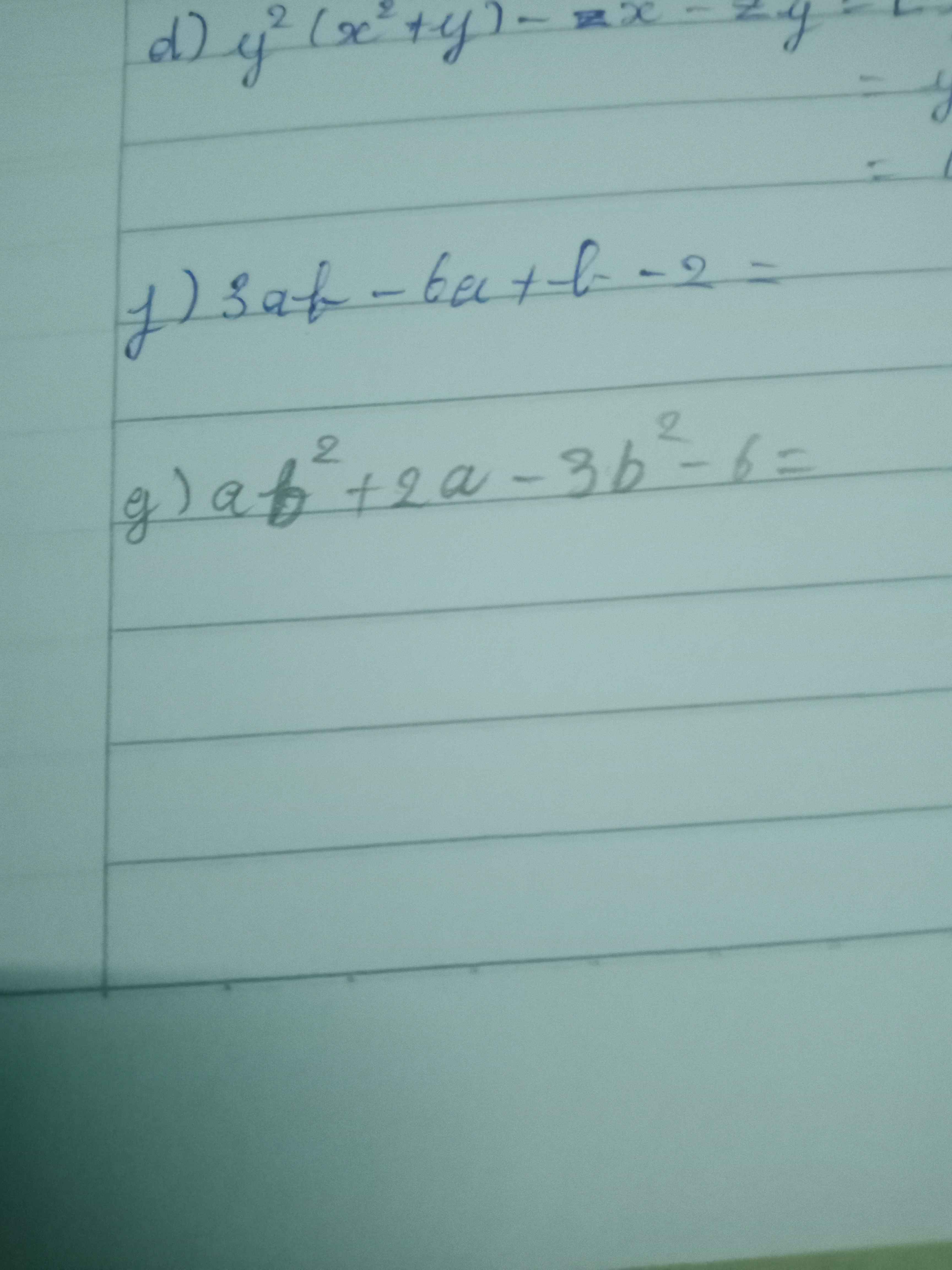
f: \(3ab-6a+b-2\)

\(=3a\left(b-2\right)+\left(b-2\right)\)

\(=\left(b-2\right)\left(3a+1\right)\)

Bài 3: 

a: Gọi OK là khoảng cách từ O đến AB

Suy ra: K là trung điểm của AB

hay \(AK=BK=\dfrac{AB}{2}=\dfrac{8}{2}=4\left(cm\right)\)

Áp dụng định lí Pytago vào ΔOKA vuông tại K, ta được:

\(OA^2=OK^2+KA^2\)

hay OK=3(cm)

Bài 6:

a) Xét ΔBAC vuông tại A và ΔBAD vuông tại A có 

BA chung

AC=AD(gt)

Do đó: ΔBAC=ΔBAD(hai cạnh góc vuông)

Suy ra: \(\widehat{CBA}=\widehat{DBA}\)(hai góc tương ứng)

hay BA là tia phân giác của \(\widehat{DBC}\)

Các số được điền vào các ô theo thứ tự từ trái sang phải là:

-1; - \(\dfrac{1}{3}\);  \(\dfrac{2}{3}\); \(\dfrac{4}{3}\)

- Xét : \(x^2+8x-20\le0\)

\(\Rightarrow-10\le x\le2\)

Mà \(x>0\)

\(\Rightarrow0< x\le2\)

- Xét  \(x^2-2\left(m+3\right)x+m^2-2m< 0\)

Có : \(\Delta^,=b^{,2}-ac=\left(m+3\right)^2-\left(m^2-2m\right)\)

\(=m^2+6m+9-m^2+2m=8m+9\)

- Để bất phương trình có nghiệm

\(\Leftrightarrow\Delta>0\)

\(\Leftrightarrow m>-\dfrac{9}{8}\)

=> Bất phương trình có nghiệm \(S=\left(x_1;x_2\right)\)

Mà \(0< x\le2\)

\(\Rightarrow0< x_1< x_2\le2\)

\(TH1:x=2\)

\(\Rightarrow4-4\left(m+3\right)+m^2-2m< 0\)

\(\Rightarrow3-\sqrt{17}< m< 3+\sqrt{17}\)

\(TH2:0< x_1< x_2< 2\)

\(\Rightarrow\left\{{}\begin{matrix}m^2-2m>0\\m^2-6m-8>0\\0< 2\left(m+3\right)< 2\end{matrix}\right.\)

\(\Rightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}m< 0\\m>2\end{matrix}\right.\\\left[{}\begin{matrix}m>3+\sqrt{17}\\m< 3-\sqrt{17}\end{matrix}\right.\\-3< m< -2\end{matrix}\right.\)

Vậy \(3-\sqrt{7}< m< 3+\sqrt{7}\)

Từ pt đầu \(\Rightarrow-10\le x\le2\) (1)

Để BPT chứa m có nghiệm thì \(\Delta'>0\Rightarrow m...\) (2)

Gọi 2 nghiệm của pt chứa m là \(x_1;x_2\Rightarrow\) miền nghiệm của BPT dưới là \(D=\left(x_1;x_2\right)\)

Do (1) chỉ chứa 2 số nguyên dương là 1 và 2, nên để hệ có nghiệm nguyên dương thì D cần chứa ít nhất 1 trong 2 giá trị 1 hoặc 2

\(\Leftrightarrow\left[{}\begin{matrix}x_1< 1< x_2\\x_1< 2< x_2\end{matrix}\right.\) (các trường hợp trùng lặp 2 điều kiện ví dụ \(x_1< 1< 2< x_2\) không thành vấn đề vì cuối cùng ta cũng hợp nghiệm)

\(\Leftrightarrow\left[{}\begin{matrix}f\left(1\right)< 0\\f\left(2\right)< 0\end{matrix}\right.\) (3) với \(f\left(x\right)=x^2-2\left(m+3\right)x+m^2-2m\)

Lấy giao nghiệm của (2) và (3) sẽ được khoảng m cần tìm