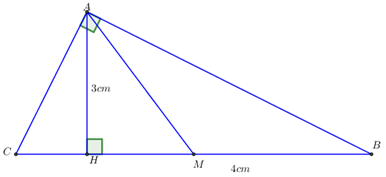
tính diện tích tam giác ABCD biết AB=3cm , AC =5cm , đường trung tuyến AM=2cm

Những câu hỏi liên quan
Tính diện tích tam giác ABC biết AB=3cm,AC= 5cm ,đường trung tuyến AM =2cm.
Đố ai giải được bài này
Tính S tam giác ABC biết AB = 3cm, AC = 5cm và đường trung tuyến AM = 2cm
Cho tam giác ABC, AB= 3cm , AC= 5cm, trung tuyến AM = 2 cm. Tính diện tích tam giác ABC.
diện tích tam giác là 3.5=15(cm )thế nha bạn dễ ọt yk
d
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho tam giác ABC vuông tại A,biết AB=3cm,BC=5cm,đường trung tuyến AM
a)tính AM?
b)tính diện tích tam giác ABC?
a)Vì AM là đường trung tuyền nên ta có
AM=1/2BC
AM=(1/2).5 => AM=2,5(cm)
b)áp dụng định lý Pytago vào tam giác ABC vuông tại A ta có
AB^2+AC^2=BC^2
thay số ta có : 3^2+AC^2=5^2=>9+AC^2=25=>AC^2=25-9=16
=>AC= căn bậc 2 của 16
=>AC=4(cm)
diện tích tam giác ABC là:
S=1/2a.h=1/2.3.4=6(cm2)
Hết nhé ^_^
Đúng 1
Bình luận (0)
ta có tam giác ABC vuông tại A
Áp dụng tỉ số lượng giác trong .........................
=> AM2=BM.BC
=>AM=\(\sqrt{2,5\times5}\approx3,6cm\)
diện tích tam giác vuông ABC là
STAM GIÁC ABC=\(\frac{1}{2}AM.BC=9cm^2\)
Đúng 0
Bình luận (0)
a) Ta có tam giác ABC vuông tại A có:
Đường trung tuyến AM ứng với cạnh huyền BC
=> AM = 1/2 BC = 5/2 = 2,5 (cm)
b) Xét tam giác ABC vuông tại A, ta có:
BC2 = AB2 + AC2
52 = 32 + AC2
AC2 = 25 - 9 = 16
=> AC = 4 (cm)
Diện tích tam giác vuông ABC là:
SABC = 1/2 x (3+4) = 1/2 x 12 = 6 (cm2)
Đáp số: a) 2,5 cm
b) 6 cm2
Đúng 0
Bình luận (0)
Cho tam giác ABC biết AB=4cm, BC= 5cm, AC=8cm. AM là đường trung tuyến của tam giác ABC
a. Hãy tính diện tích tam giác ABC
b) tính độ dài đường trung tuyến AM
a, Diện tích tam giác ABC là :
S ABC^2 = (4+5+8)/2 . [(4+5+8)/2-4] . [(4+5+8)/2-5] . [(4+5+8)/2-6]
= 8,5 . 4,5 . 3,5 . 0,5 = 669,375 ( công thức hê-rông rùi bình phương 2 vế lên )
=> S ABC = 25,87228247 (cm2)
Tk mk nha
Đúng 0
Bình luận (0)
Cho tam giác vuông tại A (AB <AC) có đường cao AH và AH =2cm, BC =5cm
a) tính đọ dài BH, CH, AB, AC
b) vẽ trung tuyến AM. Tìm số đa AMH^
c) tính diện tích tam giác AHM
hình tự vẽ nhé
a) \(AB< AC\) => \(BH< CH\)
Áp dụng hệ thức lượng vào tam giác vuông ABC ta được:
\(AH^2=BH.CH\)
=> \(BH.CH=4\)
mà \(BH+CH=5\),
giải ra ta được: \(BH=1cm;\)\(CH=4cm\)
Áp dụng hệ thức lượng vào tam giác vuông ABC đc:
AB2 = BH . BC
=> AB2 = 1 . 5 = 5
=> \(AB=\sqrt{5}cm\)
Tương tự đc: \(AC=2\sqrt{5}cm\)
Đúng 0
Bình luận (0)
b) Tam giác ABC có AM là trung tuyến
=> AM = BM = MC = BC/2 = 2,5 cm
\(\sin AMH=\frac{AH}{AM}=\frac{2}{2,5}=0,8\)
=> \(\widehat{AMH}\approx53^08'\)
c) \(HM=BM-BH=2,5-1=1,5cm\)
\(S_{\Delta AHM}=\frac{AH.HM}{2}=\frac{2.1,5}{2}=1,5cm^2\)
Đúng 0
Bình luận (0)
Bài 1: Cho tam giác ABC vuông tại A, trung tuyến AM =5cm, AC=6cm . Giải tam giác ?
Bài 2 : Cho hcn ABCD, góc BAC =30 , AC=10cm. Tính chu vi và diện tích hcn ABCD.
Bài 3 : Cho ABCD , A=D=90 độ . C=40 độ, AB =4cm, AD= 3cm. Tính diện tích ABCD.
giải từng bước nha....
AM = 5 => BC = 10
Dung py ta go tính ra AB
Tính các góc còn lại nhờ 3 cạnh vừa tính dùng hàm cos ; sin gì đó
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A có đường cao AH và đường trung tuyến AM. Biết AH=3cm; HB=4cm. Hãy tính AB,AC,AM và diện tích tam giác ABC
\(HC=\dfrac{3^2}{4}=2.25\left(cm\right)\)
BC=HB+HC=6,25(cm)
AM=BC/2=3,125(cm)
\(AB=\sqrt{4\cdot6.25}=5\left(cm\right)\)
\(AC=\sqrt{6.25^2-5^2}=3.75\left(cm\right)\)
Đúng 4
Bình luận (0)
+ ) áp dụng định lí Pytago trong tam giác vuông \(ABH\) vuông tại \(H\) , ta có :
\(AB^2=AH^2+HB^2=3^2+4^2=25\Rightarrow AB=5\left(cm\right)\)
+ ) áp dụng hệ thức về cạnh và đường cao trong tam giác vuông \(ABC\) với \(AH\) là đường cao , ta có :
\(\dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\)
\(\Leftrightarrow\) \(\dfrac{1}{AC^2}=\dfrac{1}{AH^2}-\dfrac{1}{AB^2}\)
\(\Leftrightarrow\) \(\dfrac{1}{AC^2}=\dfrac{1}{3^2}-\dfrac{1}{5^2}=\dfrac{16}{225}\)
\(\Rightarrow AC=\dfrac{15}{4}\left(cm\right)\)
+ ) áp dụng định lí Pytago trong tam giác vuông \(ABC\) vuông tại \(A\) , ta có :
\(BC^2=AB^2+AC^2=5^2+\left(\dfrac{15}{4}\right)^2=\dfrac{625}{16}\)
\(\Rightarrow BC=\dfrac{25}{4}\left(cm\right)\)
+ ) tam giác \(ABC\) vuông tại \(A\) có trung tuyến \(AM\) nên ta có :
\(AM=\dfrac{1}{2}BC=\dfrac{25}{8}\left(cm\right)\)
Đúng 2
Bình luận (1)
Cho tam giác ABC vuông tại A có đường cao AH và đường trung tuyến AM .Biết AH = 3cm, HB = 4 cm. Hãy tính AB AC AM , và diện tích tam giác ABC .
Xét tam giác ABH vuông tại H, ta có:
\(AB^2=AH^2+BH^2\)\(=3^2+4^2=25\)
\(\Rightarrow AB=5\left(cm\right)\)
Xét tam giác ABC vuông tại A, theo hệ thức lượng ta có:
\(AH^2=AB\cdot AC\Rightarrow AC=\dfrac{AH^2}{AB}=\dfrac{3^2}{5}=1,8\left(cm\right)\)
Do đó:\(BC=\sqrt{AB^2+AC^2}=\sqrt{5^2+1,8^2}\simeq5,3\left(cm\right)\)
AM là đường trung tuyến trong tam giác vuông ABC
=> AM=\(\dfrac{1}{2}\) BC= 2,65 \(\left(cm\right)\)
Đúng 0
Bình luận (0)